

陕西省西安市曲江第一中学2023-2024学年九年级上学期第一次月考数学试题(无答案)
展开九年级第一次数学测试试题
一、选择题(共8小题,每小题3分,计24分)
1.下列方程是一元二次方程的是( )
A. B.
C. D.
2.下列说法正确的是( )
A.四条边相等的四边形是正方形 B.一组对边平行,另一组对边相等的四边形是平行四边形
C.对角线相等的四边形是矩形 D.对角线互相垂直且平分的四边形是菱形
3.一元二次方程配方后可化为( )
A. B. C. D.
4.关于x的一元二次方程有实数根,则k的取值范围是( )
A. B. C.且 D.且
5.如图,菱形ABCD的对角线AC、BD相交于点O,,若,,则下列结论正确的是( )
A. B. C. D.
6.国家统计局统计数据显示,我国快递业务逐年增加,2020年至2022年我国快递业务收入由7500亿元增加到9000亿元.设我国2020年至2022年快递业务收入的年平均增长率为x,则可列方程为( )
A. B.
C. D.
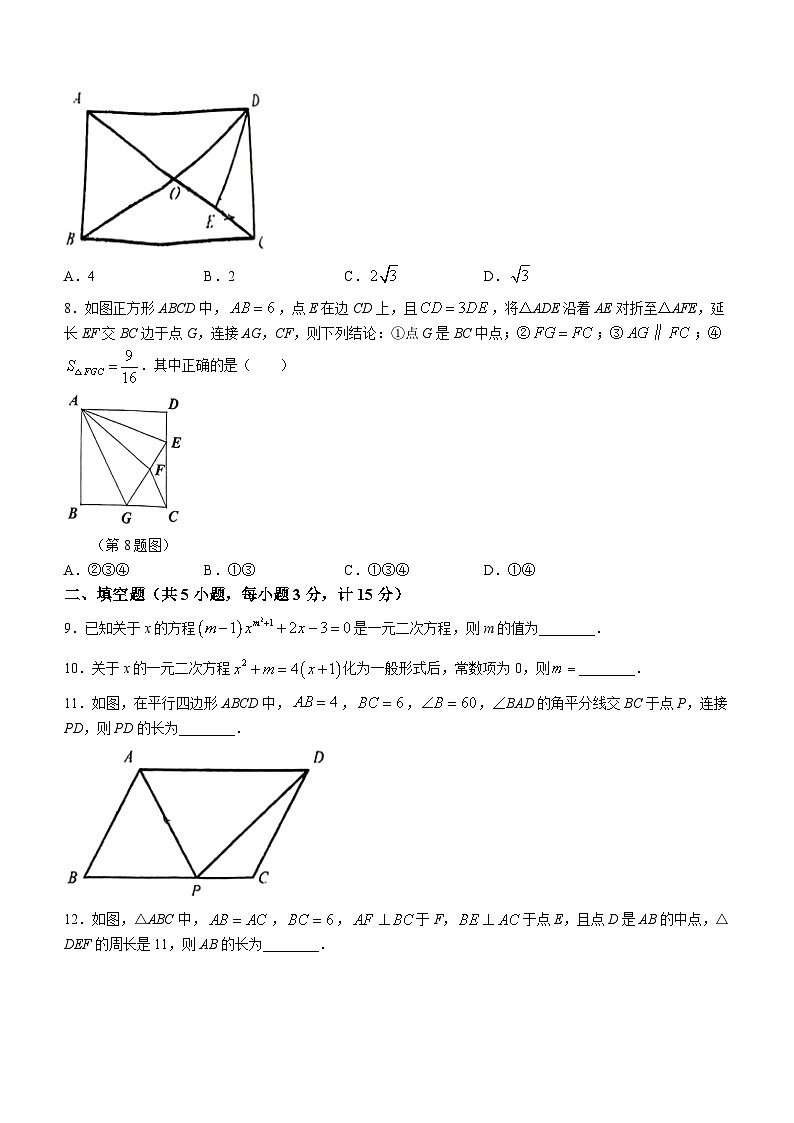
7.如图,在矩形ABCD中,,对角线AC与BD相交于点O,,垂足为E,,则DE的长( )
A.4 B.2 C. D.
8.如图正方形ABCD中,,点E在边CD上,且,将△ADE沿着AE对折至△AFE,延长EF交BC边于点G,连接AG,CF,则下列结论:①点G是BC中点;②;③;④.其中正确的是( )
(第8题图)
A.②③④ B.①③ C.①③④ D.①④
二、填空题(共5小题,每小题3分,计15分)
9.已知关于x的方程是一元二次方程,则m的值为________.
10.关于x的一元二次方程化为一般形式后,常数项为0,则________.
11.如图,在平行四边形ABCD中,,,,∠BAD的角平分线交BC于点P,连接PD,则PD的长为________.
12.如图,△ABC中,,,于F,于点E,且点D是AB的中点,△DEF的周长是11,则AB的长为________.
(第12题图)
13.如图,在矩形ABCD中,,,点P在AD上,点Q在BC上,且连接CP,QD,则的最小值为________.
(第13题图)
三、解答题(共13题,计81分,解答题应写出过程)
14(10分).选择适当的方法求解下列一元二次方程.
(l)
(2)
15(5分).已知四边形ABCD中,,请用尺规作图的方法,在AB边上求作一点E,使得(不写作法,保留作图痕迹).
16(5分).如图,在正方形ABCD中,点E在BC边的延长线上,点F在CD边的延长线上,且,连接AE和BF相交于点M,AE与BF之间数量相等吗?请说明理由.
17(5分).如图,有一块长20cm,宽10cm的长方形铁皮,若在铁皮的四个角上各截去一个相同的小正方形,然后把凸出部分折起来,做成一个底面积为的无盖的长方体盒子,求这个盒子的高.
18(5分).等腰三角形底边长为3,两条腰长是关于x的一元二次方程的两个根,求该三角形的周长.
19(5分).如图,在正方形ABCD中,等边三角形AEF的顶点E,F分别在边BC和CD上,求∠CEF的度数.
20(5分).二十四节气是中华上古农耕文明的智慧结晶,被国际气象界誉为“中国第五大发明”.小华购买了二十四节气主题邮票,他将“立春”“清明”“雨水”三张纪念邮票(除正面内容不同外,其余均相同)背面朝上,洗匀放好.
(1)小华从中随机抽取一张邮票是“立春”的概率是________.
(2)小华从中随机抽取一张邮票,记下内容后,正面向下放回,洗匀后再从中随机抽取一张邮票,请用画树状图或列表的方法,求小华两次抽取的邮票中,一张是“立春”,一张是“雨水”的概率.
21(5分).已知关于x的一元二次方程的两实数根为x且满足,,求的值.
22(7分).如图平行四边形ABCD中,,,垂足分别是点E,F,且满足.
(1)求证:四边形ABCD是菱形:
(2)若,,求四边形ABCD的面积.
23(6分).如图,在△ABC中,,BD平分∠ABC.四边形ABED是平行四边形,DE交BC于点F,连接CE.求证:四边形BECD是矩形.
24(6分).2023年杭州亚运会于9月23日至10月8日浙江杭州举行,名为“忆江南”的三个吉祥物为“宸宸”、“琮琮”、“莲莲”,聚焦共同的文化基因,蕴含独特的城市元素.亚运会开幕以来,某商店平均每天可销售吉祥物20个,每个盈利40元.调查发现:在每个吉祥物降价幅度不超过10元的情况下,每下降2元,每天可多售出10个,如果每天要盈利1440元,则每个吉祥物应降价多少元?
25(7分).阅读下面的例题:
例:解分程
解:①当时,原方程可化为,解得(舍去),;
②当时,原方程可化为,解得(舍去),;
综上所述,原方程的根是,.
依照题目所给出的例题解法,解方程.
26(10分).如图,在Rt△ABC中,,,点D在边AC上(不与点A,C重合),连接BD,点K为线段BD的中点,过点D作于点E,连接CK,EK,CE.
图1 图2 图3
(1)如图1,若,则△ECK的形状为________.
(2)如图2,若,将△ADE绕点A顺时针旋转一定的角度(旋转角小于90°),使得D,E,B三点共线,点K为线段BD的中点,点M为线段BD上一点,且满足,△ECK的形状是否发生改变?请说明理由.
如图3,Rt△ABC中,若,,点D在边AC上(不与点A,C重合),满足,将线段AD绕点A旋转,点K始终为BD的中点,则线段CK长度的最大值是多少?请直接写出结果
陕西省西安市铁一中学(曲江校区)2023-2024学年八年级下学期第一次月考数学试题(无答案): 这是一份陕西省西安市铁一中学(曲江校区)2023-2024学年八年级下学期第一次月考数学试题(无答案),共4页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
陕西省西安市曲江第一学校2023-2024学年度九年级上学期第二次月考数学试题: 这是一份陕西省西安市曲江第一学校2023-2024学年度九年级上学期第二次月考数学试题,共22页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
陕西省 西安市 雁塔区西安市曲江第一中学2023-2024学年上学期八年级期中数学试题: 这是一份陕西省 西安市 雁塔区西安市曲江第一中学2023-2024学年上学期八年级期中数学试题,共2页。












