初中苏科版5.4 主视图、左视图、俯视图综合训练题
展开5.4主视图、左视图、俯视图随堂练习-苏科版数学七年级上册
学校:___________姓名:___________班级:___________考号:___________
一、单选题
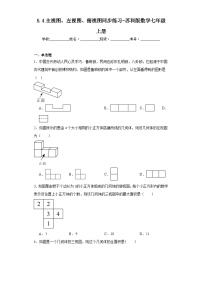
1.一个长方体从左面看,上面看到的相关数据如图所示,则其从正面看到的图形面积是( )
A.6 B.8 C.12 D.24
2.如图,是由4个大小相同的正方体组合而成的几何体,其主视图是( )
A. B. C. D.
3.如图是由5个大小相同的正方体组合而成的几何体,其俯视图是( )
A. B. C. D.
4.下列四个几何体的俯视图中与众不同的是( )
A. B. C. D.
5.下图所示的几何体的主视图是( )
A. B. C. D.
6.如图所示的几何体的左视图是( )
A. B. C. D.
7.下列是由4个大小相同的小立方块搭成的几何体,从正面和从左面看得到的形状图相同的是( )
A. B. C. D.
8.如图所示的零件,其主视图正确的是( )
A. B. C. D.
9.砚台与笔、墨、纸是中国传统的文房四宝,是中国书法的必备用具.如图是一方寓意“规矩方圆”的砚台,它的俯视图是( )
A. B. C. D.
10.如图所示的几何体,它的左视图是( )
A. B. C. D.
二、填空题
11.若正方体棱长的和是36,则它的体积是 .
12.从棱长为4的正方体毛坯的一角,挖去一个棱长为2的小正方体,得到一个如图所示的零件,则这个零件的表面积为 .
13.下列几何体中,仅主视图与左视图相同的是 .(填序号)
14.如图是一个圆柱体的三视图,由图中数据计算此圆柱体的侧面积为 .(结果保留π)
15.一个几何体由若干个大小相同的小立方块搭成,从上面和从左面看到的这个几何体的形状图如图所示,请搭出所有满足条件的几何体,则搭出的几何体由 个小立方块构成.
16.观察图中的物体, 是从正面看到的, 是从左面看到的, 是从上面看到的.
17.已知某几何体的三视图如图所示,其中俯视图为正六边形,则该几何体的侧面积为 .
18.一个几何体的三视图如图所示,则这个儿何体的侧面积是 cm2.
19.如图,这是由几个相同的小正方体堆成的物体的两种视图,那么堆成这个物体的小正方体的个数可能是 .
20.如图所示是某种型号的正六角螺母毛坯的三视图,则它的侧面积为 .
三、解答题
21.用若干个完全相同的小正方体搭成一个几何体,当从正面、上面看这个几何体时,得到的图形如图,问:在这个几何体中,小正方体的个数最多是多少?最少是多少?
22.如图是一立体图形的三视图,用橡皮泥或其他物品作出它的模拟图.
23.由7个相同的小立方块搭成的几何体如图所示,
(1)请画出从它的正面、上面、左面看到的图形.
(2)计算它表面积(棱长为1),
24.在平整的地面上,有一个由若干个完全相同的小立方块搭成的几何体,如图所示.请画出这个几何体从三个方向看到的形状图.
25.如图,是一个立体图形的三视图,由图形显示的数据求这个立体图形的表面积(用含的式子表示)
参考答案:
1.B
【分析】先根据从左面、从上面看到的形状图的相关数据可得,从正面看到的形状图是长为4宽为2的长方形,再根据长方形的面积公式计算即可.
【详解】解:根据从左面、从上面看到的形状图的相关数据可得:
从正面看到的形状图是长为4宽为2的长方形,
则从正面看到的形状图的面积是4×2=8;
故选B.
【点睛】本题主要考查了由三视图判断几何体,长方形的面积公式,掌握三视图判断几何体,长方形的面积公式是解题的关键.
2.D
【分析】根据几何体的三视图,即可解答.
【详解】解:根据图形可得主视图为:
故选:D.
【点睛】本题考查了几何体的三视图,掌握画物体的三视图的的方法是解题的关键,画物体的三视图的口诀为:主、俯:长对正;主、左:高平齐;俯、左:宽相等.
3.C
【分析】根据俯视图是从上面看到的图形进行求解即可.
【详解】解:从上面看,看到的图形有2行2列共3个小正方形,即看到的图形为: ,
故选:C.
【点睛】本题主要考查了小正方体堆砌成的图形的三视图,熟知俯视图是从上面看到的图形是解题的关键.
4.B
【详解】解:根据从上边看得到的图形是俯视图,可得
A的俯视图是第一列两个小正方形,第二列一个小正方形,
B的俯视图是第一列是两个小正方形,第二列是两个小正方形,
C的俯视图是第一列两个小正方形,第二列一个小正方形,
D的俯视图是第一列两个小正方形,第二列一个小正方形,
故选B.
【点睛】本题考查简单组合体的三视图.
5.D
【分析】主视图是从物体正面看,所得到的图形.
【详解】观察图形可知,几何体的主视图为
.
故选:D.
【点睛】本题考查了几何体的三种视图,掌握定义是关键.注意所有的看到的棱都应表现在三视图中.
6.B
【分析】根据左视图是从左面看到的图形判定则可.
【详解】解:从左边看:可以看到一个正方形,里面是宽以虚线呈现的矩形,
所以左视图是:
故选:B.
【点睛】本题考查了简单组合体的三视图,掌握三视图是解题的关键.
7.C
【分析】根据主视图及左视图的定义求解即可.
【详解】A. 从正面看有两行组成,上面一行是一个小正方形,下面一行是三个小正方形;从左面看也有两行组成,上面一行是一个小正方形,下面一行是1个小正方形,所以不符合题意.
B. 从正面看有三行组成,上面两行是各有1个小正方形,最下面一行是两个小正方形;从左面看也有三行组成,每行都只是一个小正方形,不符合题意.
C从正面看第一层是两个小正方形,第二层是一个小正方形;从左边看第一层是两个小正方形,第二层是一个小正方形.
D. 从正面看有两行组成,上面一行靠右侧一个小正方形,下面一行是两个小正方形;从左面看也有两行组成,上面一行左侧一个小正方形,下面一行是2个小正方形,所以不符合题意.
故选C.
【点睛】本题考查了简单组合体的三视图.
8.D
【分析】主视图是从正面看,得到的平面图形为所求.
【详解】主视图是从正面看,得到
故选:D
【点睛】考核知识点:三视图.理解三视图的意义,注意观察的角度.
9.C
【分析】根据俯视图是从物体的上面看的图形即可解答.
【详解】解:∵从砚台上面看到的图形是
故选.
【点睛】本题考查了俯视图的概念,理解俯视图的概念是解题的关键.
10.C
【分析】根据左视图的定义:一般指由物体左边向右做正投影得到的视图,即可得出结论.
【详解】解:根据左视图的定义,C选项为几何体的左视图
故选C.
【点睛】此题考查的是判断几何体的左视图,掌握左视图的定义是解决此题的关键.
11.27
【分析】首先用棱长总和除以12求出棱长,再根据正方体的体积公式,把数据代入公式解答.
【详解】36÷12=3,
V=a3=3×3×3=27,
它的体积是27.
【点睛】本题考查的是正方体的体积公式,熟练掌握这一点是解题的关键.
12.96
【分析】从棱长为4的正方体毛坯的一角,挖去一个棱长为2的小正方体,得到的几何体的表面积,仍然可以看作是原正方体的表面积,根据正方体的表面积的计算方法,即可.
【详解】解:∵从棱长为4的正方体毛坯的一角,挖去一个棱长为2的小正方体,得到的几何体的表面积,仍然可以看作是原正方体的表面积,
∴这个零件的表面积=6×4×4=96.
故答案为96.
【点睛】本题主要考查正方体的表面积的计算,把从棱长为4的正方体毛坯的一角,挖去一个棱长为2的小正方体,得到的几何体的表面积,仍然可以看作是原正方体的表面积,是解题的关键.
13.③④
【分析】分别画出立体图的三视图即可解题.
【详解】的俯视图、左视图、主视图都是
的俯视图、左视图、主视图都是
的俯视图是,左视图、主视图都是
的俯视图是,左视图、主视图都是
仅主视图与左视图相同的是③④
故答案为:③④.
【点睛】本题考查简单几何体的三视图,是重要考点,难度较易,掌握相关知识是解题关键.
14.24π
【详解】解:由图可知,圆柱体的底面直径为4,高为6,所以,侧面积=4π×6=24π.故答案为24π.
点睛:本题考查了立体图形的三视图和学生的空间想象能力,圆柱体的侧面积公式,根据主视图判断出圆柱体的底面直径与高是解题的关键.
15.5或6
【详解】由几何体的俯视图和左视图可知主视图的列数与俯视数的列数相同,左视图的列数与俯视图的行数相同,所以俯视图中该列小正方形数字如图所示,或或,即可画出几何体.
解:搭建的几何体,如图所示:
搭出的几何体由5或6个小立方块构成,
故答案为:5或6.
【点睛】本题考查几何体的三视图画法.由几何体的俯视图和左视图可知主视图的列数与俯视数的列数相同,左视图的列数与俯视图的行数相同,且每列小正方形数目为俯视图中相应行中正方形数字中的最大数字.
16. c b a
【详解】【分析】观察右面的图形可得:从左面看到的图形是上竖着下横着的2个长方形,从上面看到的是一个圆和一个长方形,从正面看到是上竖着下横着的2个长方形,下面长方形的长比较长.
【详解】观察图中的物体,c是从正面看到的,b是从左面看到的,a是从上面看到的.
故答案为(1). c (2). b (3). a
【点睛】此题考查了从不同方向观察物体和几何体.锻炼了学生的空间想象力和抽象思维能力.
17.108
【分析】观察该几何体的三视图发现该几何体为正六棱柱,然后根据提供的尺寸求得其侧面积即可.
【详解】观察该几何体的三视图发现该几何体为正六棱柱,其底面边长为3,高为6,
所以其侧面积为3×6×6=108,
故答案为:108
【点睛】本题考查了由三视图判断几何体的知识,解题的关键是能够根据三视图判断几何体的形状及各部分的尺寸,难度不大.
18.14π
【分析】首先判断几何体的形状,然后根据其尺寸求得其侧面积即可.
【详解】解:观察三视图发现该几何体为圆锥,其底面直径为4cm,母线长为7cm,
∴侧面积为:,
故答案为:14π.
【点睛】本题考查由三视图判断几何体,圆锥的有关计算,由该三视图中的数据确定底面直径和母线长是解本题的关键.
19.4或5/5或4
【分析】根据正视图和俯视图可得这个物体的底层有3个小正方体,第二层可能有1个或2个小正方形,即可求解.
【详解】解:由图可得,这个物体的底层有3个小正方体,第二层可能有1个或2个小正方形,
∴堆成这个物体的小正方体的个数可能是4或5.
【点睛】本题考查三视图的灵活运用,同时体现对空间想象能力方面的考查,熟练掌握口诀:俯视图打地基,正视图疯狂盖,左视图拆违章更容易得到答案.
20.36
【分析】正六角螺母侧面为6个相同的长方形,求出每个长方形的面积,即可得出它的侧面积.
【详解】2×3=6cm2,
6×6=36cm2.
故答案为:36.
【点睛】本题主要考查正六棱柱的三视图,将三视图上边的长度转化为正六棱柱对应边的长度是解题关键.
21.最多5个;最少4个
【分析】从正面看时,图形左列最多有2个小正方体,右列有1个正方体,将小正方体可能的个数分别标记在从上面看的图形上.
【详解】解:根据已知可得,在从上面看到的图形中,各位置上小正方体的个数最多时如图D1-3(1),各位置上小正方体的个数最少时如图D1-3(2)
由图(1)可知,这个几何体中有5个小正方体;由图(2)可知,这个几何体中有4个小正方体,即在这个几何体中,小正方体的个数最多是5,最少是4
22.三棱柱.
【分析】主视图、左视图、俯视图是分别从物体正面、左面和上面看,所得到的图形,根据给出的三视图,分析、判定即可.
【详解】解:解:根据主视图和左视图为矩形判断出是柱体,根据俯视图是三角形可判断出这个几何体应该是三棱柱.
【点睛】本题考查由三视图判定几何体,是锻炼学生的抽象思维能力和空间想象能力.
23.(1)见详解;(2)28
【分析】(1)根据三视图的定义及其分布情况作图可得;
(2)将三个方向上的面积相加,再乘以2,然后加上凹进去的两个面可得其表面积.
【详解】解:(1)该几何体的三视图如图所示:
(2)其表面积为2×(5+5+3)+2=28.
【点睛】本题主要考查作图−三视图,解题的关键是熟练掌握三视图的定义及表面积的求法.
24.见解析
【分析】根据三视图的画法,分别画出从正面、左面、上面看到的图形即可.
【详解】解:这个几何体从三个方向看到的图形如下:
【点睛】本题考查了简单组合体的三视图,正确掌握不同视图的观察角度是解题关键.
25. cm2
【分析】从三视图可以看正视图以及左视图为矩形,而俯视图为圆形,故可以得出该立体图形为圆柱.由三视图可以圆柱的半径,长和高,易求侧面积.
【详解】该立体图形为圆柱,
∵圆柱的底面半径,高,
∴圆柱的侧面积为:cm2.
∴圆柱的表面积为 cm2.
【点睛】此题主要考查了圆柱的有关计算以及由三视图判断几何体,同时也体现了对空间想象能力方面的考查,难度不大.
苏科版七年级上册第5章 走进图形世界5.4 主视图、左视图、俯视图课后测评: 这是一份苏科版七年级上册第5章 走进图形世界5.4 主视图、左视图、俯视图课后测评,共7页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
数学苏科版5.4 主视图、左视图、俯视图练习: 这是一份数学苏科版5.4 主视图、左视图、俯视图练习,共7页。试卷主要包含了单选题,填空题,解答题等内容,欢迎下载使用。
初中数学苏科版七年级上册第5章 走进图形世界5.4 主视图、左视图、俯视图课后复习题: 这是一份初中数学苏科版七年级上册第5章 走进图形世界5.4 主视图、左视图、俯视图课后复习题,共6页。试卷主要包含了单选题,填空题,解答题等内容,欢迎下载使用。