

广东省深圳市南山区华侨城中学深湾部+2023—2024学年上学期月考九年级数学试题
展开华侨城中学深湾部 初三年级
姓名: 班级:
一、单选题
1.已知是一元二次方程的一个根,则的值为( )
A.或2 B. C.2 D.0
2.用公式法解一元二次方程时,首先要确定,,的值,下列叙述正确的是( )
A.,, B.,,
C.,, D.,,
3.已知关于的一元二次方程的两根分别为,,则原方程可化为( )
A. B.
C. D.
4.如图,有甲、乙、丙个转盘,这个转盘在转动过程中指针停在黑色区域的可能性( )
A.甲转盘最大 B.乙转盘最大
C.丙转盘最大 D.甲、乙、丙转盘一样大
5.投掷一枚质地均匀的硬币次,正面向上次,下列表达正确的是( )
A.的值一定是 B.的值一定不是
C.越大,的值越接近 D.随着的增加,的值会在附近摆动,呈现出一定的稳定性
6.已知关于的方程的一个根为,则它的另一个根及的值分别是( )
A.和 B.和1 C.1和 D.1和1
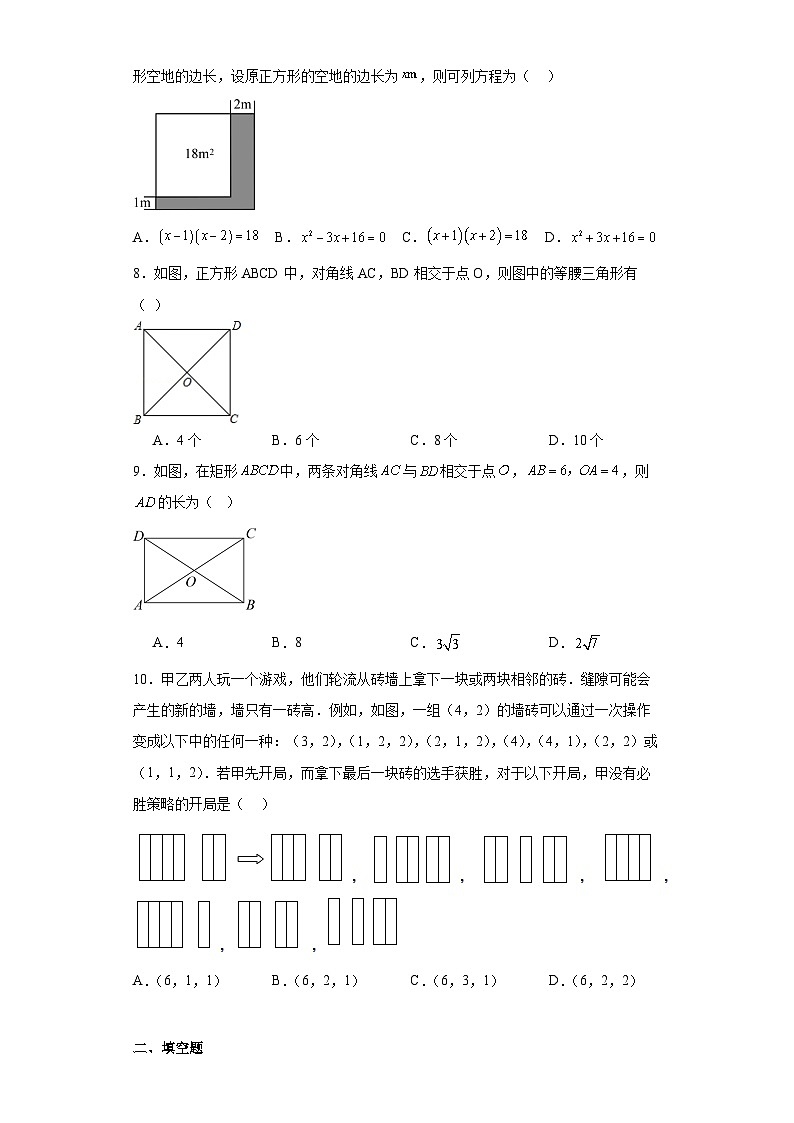
7.公园有一块正方形的空地,后来从这块空地上划出部分区域栽种鲜花(如图阴影部分),原空地一边减少了,另一边减少了2,剩余空地的面积为18,求原正方形空地的边长,设原正方形的空地的边长为,则可列方程为( )
A. B. C. D.
8.如图,正方形ABCD中,对角线AC,BD相交于点O,则图中的等腰三角形有( )
A.4个 B.6个 C.8个 D.10个
9.如图,在矩形中,两条对角线与相交于点,,则的长为( )
A.4 B.8 C. D.
10.甲乙两人玩一个游戏,他们轮流从砖墙上拿下一块或两块相邻的砖.缝隙可能会产生的新的墙,墙只有一砖高.例如,如图,一组(4,2)的墙砖可以通过一次操作变成以下中的任何一种:(3,2),(1,2,2),(2,1,2),(4),(4,1),(2,2)或(1,1,2).若甲先开局,而拿下最后一块砖的选手获胜,对于以下开局,甲没有必胜策略的开局是( )
A.(6,1,1) B.(6,2,1) C.(6,3,1) D.(6,2,2)
二、填空题
11.在一个有10万人的小镇上,随机调查人,期中有人看当地电视台的《早间新闻》,在该镇随便问一人,他看《早间新闻》的概率大约是 .
12.一个密码锁的密码由四个数字组成,每个数字都是这十个数字中的一个,只有当四个数字与所设定的密码相同时,才能将锁打开,粗心的小张忘记了后两个数字,他一次就能打开该锁的概率是 .
13.五个连续整数,前三个数的平方和等于后两个数的平方和,你能求出这五个整数分别是多少吗?
14.已知,是关于的一元二次方程的两个实数根,且.则的值为 .
15.如图,一次函数的图象交x轴于点A,交y于点B,点P在线段上(不与点A、B重合),过点P分别作和的垂线,垂足为C、D,若矩形的面积为1时,则点P的坐标为 .
华侨城中学深湾部 初三年级
姓名: 班级:
题目 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
答案 |
|
|
|
|
|
|
|
|
|
|
11. 12. 13 14 15
三、解答题
16.按指定方法解方程:
(配方法); (公式法)
3x(x﹣1)=2﹣2x(适当方法); 2x2﹣x﹣1=0(配方法)
17.一次会议上,每两个参加会议的人都相互握了一次手,有人统计一共握了66次手.这次会议到会的人数是多少?
18.某次演讲比赛中,只有甲、乙、丙三位同学进入决赛,他们通过抽签决定演讲顺序,用画树状图法求:
(1)甲第二个出场的概率;
(2)丙在乙前面出场的概率.
19.在一个不透明的口袋里装有黑、白两种颜色的球共4个.某学习小组做摸球实验,将球搅匀后从中随机摸出一个球记下颜色,再把它放回口袋中,不断重复.下表是活动进行中的一组统计数据:
摸球的次数n | 2048 | 4040 | 10000 | 12000 |
摸到白球的次数m | 1061 | 2048 | 4979 | 6019 |
摸到白球的频率 | 0.518 | 0.5069 | 0.4979 | 0.5016 |
(1)请估计:当很大时,摸到白球的频率将会接近 (精确到);
(2)试估算口袋中白球有多少个?
(3)若从中摸出一个球后不放回,再从余下的球中摸出一个,请用列表法求两次摸到的球的颜色相同的概率.
20.某军舰以的速度由西向东航行,一艘电子侦察船以的速度由南向北航行,它能侦察出周围(包括)范围内的目标.如图,当该军舰行至A处时,电子侦察船正位于A处正南方向的B处,且.如果军舰和侦察船仍按原速度沿原方向继续航行,那么航行途中侦察船能否侦察到这艘军舰?如果能,最早何时能侦察到?如果不能,请说明理由.
21.某批发市场礼品柜台春节期间购进大量贺年卡,一种贺年卡平均每天可售出500张,每张赢利0.3元,为了尽快减少库存,摊主决定采取适当的降价措施,调查发现,如果这种贺年卡的售价每降价0.05元,那么平均每天可多售出200张.摊主要想平均每天赢利180元,每张贺年卡应降价多少元?
22.如图,一艘轮船以的速度沿既定航线由西向东航行,途中接到台风警报,某台风中心正以的速度由南向北移动,距台风中心的圆形区域(包括边界)都属台风影响区.当这艘轮船接到台风警报时,它与台风中心的距离,此时台风中心与轮船既定航线的最近距离.
既定航线
(1)如果这艘轮船不改变航向,那么它会不会进入台风影响区?
(2)如果你认为这艘轮船会进入台风影响区,那么从接到警报开始,经过多长时间它就会进入台风影响区?
参考答案:
1.B
【分析】首先把代入解方程可得,,再结合一元二次方程定义可得的值.
【详解】解:把代入得:
,
解得:,,
是一元二次方程,
,
,
,
故选:B.
【点睛】此题主要考查了一元二次方程的解和定义,关键是注意方程二次项的系数不等于0.
2.D
【分析】先化成一般式,再确定值即可.
【详解】化成一般式,得,
故,,,
故选D.
【点睛】本题考查了化成一般式确定系数,熟练掌握一般式是解题的关键.
3.D
【分析】根据根与系数的关系,直接代入计算即可.
【详解】解:∵关于x的一元二次方程的两根分别为=2,=-3,
∴2-3=-p,2×(-3)=q,
∴p=1,q=-6,
∴原方程为,
∴原方程可化为(x-2)(x+3)=0.
故选:D.
【点睛】本题考查了根与系数的关系,解题的关键是熟练掌握根与系数的字母表达式,并会代入计算.
4.D
【分析】根据概率公式分别求出这3个转盘在转动过程中指针停在黑色区域的概率,再进行比较即可.
【详解】解:∵甲转盘指针停在黑色区域的概率为;
乙转盘指针停在黑色区域的概率为;
丙转盘指针停在黑色区域的概率为.
∴甲、乙、丙转盘一样大.
故选:D.
【点睛】本题考查的是可能性的大小,根据题意得出三种情况的概率是解答此题的关键.
5.D
【分析】根据频率与概率的关系以及随机事件的定义判断即可.
【详解】解:投掷一枚质地均匀的硬币正面向上的概率是,而投掷一枚质地均匀的硬币正面向上是随机事件,是它的频率,随着的增加,的值会在附近摆动,呈现出一定的稳定性;
故选:.
【点睛】本题考查对随机事件的理解以及频率与概率的联系与区别.解题的关键是理解随机事件是有可能发生的事件.
6.D
【分析】设另一个根为a,根据一元二次方程根与系数的关系求出a及k的值.
【详解】解:设另一个根为a,
∵方程的一个根为,
∴,
∴;
∵,
∴,
即另一个为1,k的值为1,
故选:D.
【点睛】此题考查了一元二次方程的解、一元二次方程根与系数的关系:,熟记两个关系式是解题的关键.
7.A
【分析】利用长方形的面积等于18和矩形的面积公式列出方程即可.
【详解】解:设原正方形的空地的边长为,则剩余空地的长和宽分别为和,由题意,得:;
故选A.
【点睛】本题考查根据实际问题列一元二次方程,正确的识图,找准等量关系,是解题的关键.
8.C
【详解】试题分析:先根据正方形的四边相等即对角线相等且互相平分的性质,可得AB=BC=CD=AD,AO=OD=OC=OB,再根据等腰三角形的定义即可得出图中的等腰三角形的个数.
解:∵正方形ABCD中,对角线AC,BD相交于点O,
∴AB=BC=CD=AD,AO=OD=OC=OB,
∴△ABC,△BCD,△ADC,△ABD,△AOB,△BOC,△COD,△AOD都是等腰三角形,一共8个.
故选C.
考点:正方形的性质;等腰三角形的判定.
9.D
【分析】利用矩形的性质可知对角线互相平分且,再利用勾股定理求解即可.
【详解】解:在矩形中,
故选D.
【点睛】本题主要考查矩形的性质及勾股定理,熟练掌握矩形的性质及勾股定理求直角边是解决本题的关键.
10.A
【分析】根据游戏规则总结规律然后分析各个选项得出结论即可.
【详解】解:A选项中6个连续的砖墙无论甲先拿几块对方都能拿到最后一块,后面的两个1块的砖墙需要拿两次,符合题意;
B选项中后面的一个2块连续的墙砖,一个1块的墙砖即可以分三次也能两次拿完,
∴ 6个连续的砖墙无论谁拿到最后一块,甲都能拿下最后一块砖,不符合题意;
C选项先拿走6块连续墙砖边上的两个,无论对方怎么拿都让他拿到这6块连续墙砖的最后一块,然后拿3块连续墙砖边上的两个即可保证甲能拿最后一块;不符合题意;
D选项同理B,后面的两个2块连续的墙砖,即可以分三次也能分四次拿完,
∴ 6个连续的砖墙无论谁拿到最后一块,甲都能拿下最后一块砖,不符合题意;
故选:A.
【点睛】本题主要考查推理能力,根据游戏规则总结砖墙的变化规律是解题的关键.
11./
【分析】由随机调查了人,其中人看《早间新闻》,直接利用概率公式求解即可求得答案.
【详解】解:∵ 随机调查了人,其中人看《早间新闻》,
∴ 在该镇随便问一个人,他看中央电视台早间新闻的概率大约是:,
故答案为:.
【点睛】本题考查了概率的知识.用到的知识点为:概率=所求情况数与总情况数之比.
12./0.01
【分析】根据题意可知:后两个数字共有100种情况,据此即可求得一次就能打开该锁的概率.
【详解】解:因为密码由四个数字组成,千位和百位上的数字已经确定,假设十位上的数字是0,则个位上的数字即有可能是中的一个,要试10次,同样,假设个位上的数字是1,则百位上的数字即有可能是中的一个,也要试10次,依此类推,要打开该锁需要试100次,而其中只有一次可以打开,所以,一次就能打开该锁的概率是,
故答案为:.
【点睛】本题考查了随机事件概率的求法:如果一个事件有n种可能,而且这些事件的可能性相同,其中事件A出现m种结果,那么事件A的概率.
13. 22.,,0,1,2或10,11,12,13,14
【分析】设五个连续整数为x,,根据题意,解方程得到x.
【详解】解:将这五个连续整数中的第一个数设为x,
那么其余四个数依次为,
根据题意,得.
也就是.
根据方程,
所以或.
因此这五个连续整数依次为,,0,1,2或10,11,12,13,14.
【点睛】考查一元二次方程的应用,属于基础题,关键是得到5个连续数的平方的等量关系.
14.
【分析】根据根与系数的关系即可求解.
【详解】解:∵,
,
,
,
故答案为:.
【点睛】此题主要考查一元二次方程根与系数的关系:,解题的关键是熟知根与系数的关系且能灵活应用.
15.或
【分析】先根据一次函数的解析式求出点和点B的坐标,再设点P的坐标为,从而可得,然后根据矩形的面积公式可得一个关于的一元二次方程,解方程即可得得到答案.
【详解】解:在中,当时,,当时,,
∴,
∵点P在线段上(不与点A、B重合)
∴可设点P的坐标为,
∵,
∴,
∵矩形的面积为1,
∴,
∴,
解得或,均符合题意,
当时,,则,
当时,,则,
综上所述,点P的坐标为或,
故答案为:或.
【点睛】本题考查了一次函数的几何应用、一元二次方程的应用,正确设出点P的坐标,进而表示出的长,进一步根据矩形的面积公式建立一元二次方程是解题关键.
16.(1),;(2),
【分析】(1)先把常数项移到方程的右边,再对左边进行配方,再方程的左右两边同时加上,左边是完全平方式,右边等于,可以解答;
(2)根据方程的系数特点,可先确定各个项的系数,然后求出的值,最后套用求根公式解得.
【详解】(1),
移项得,,
配方,得,
即,
所以,
解得,.
(2),
,,,
,
,
所以,.
(3)x1=1,x2=﹣;(4)x1=1,x2=﹣
【详解】解:(1)∵3x(x﹣1)=2﹣2x,
∴3x(x﹣1)+2(x﹣1)=0,
则(x﹣1)(3x+2)=0,
∴x﹣1=0或3x+2=0,
解得x1=1,x2=﹣.
(2)∵2x2﹣x﹣1=0,
∴x2﹣x=,
则x2﹣x+=,即(x﹣)2=,
∴x﹣= ,
即x1=1,x2=﹣.
【点睛】本题考查了一元二次方程的解法,熟悉配方法,公式法,因式分解法是解题的关键.
17. 12人
【详解】试题分析:设参加会议有x人,每个人都与其他(x-1)人握手,共握手次数为,根据一共握了66次手列出方程求解.
设有x人参加会议,由题意得
=66,
解得x1=12,x2=-11(舍去),
答:这次到会的人数为12人.
考点:本题考查的是一元二次方程的应用
点评:解答本题的关键是掌握计算握手次数时,每两个人之间产生一次握手现象,故共握手次数为.
18. (1)
(2)
【分析】(1)首先根据题意画出树状图,然后由树状图求得所有等可能的结果与甲第二个出场的情况,再利用概率公式即可求得答案;
(2)由(1)即可求得丙在乙前面出场的情况,再利用概率公式即可求得答案.
【详解】(1)解:画树状图得:
∵共有6种等可能的结果,甲第二个出场的有2种情况,
∴甲第二个出场的概率为:;
(2)解:∵丙在乙前面出场的有3种情况,
∴丙在乙前面出场的概率为:.
【点睛】本题考查了列表法或树状图法求概率.用到的知识点为:概率所求情况数与总情况数之比.解题的关键是正确列表或画出树状图.
19.(1)0.5
(2)估计口袋中白球的个数为2个
(3)(颜色相同)
【分析】(1)根据统计数据,当n很大时,摸到白球的频率接近0.5;
(2)利用频率估计概率,可估计摸到白球的概率为0.5,然后利用概率公式计算白球的个数;
(3)先利用列表法展示所有16种等可能的结果数,再找出两次摸到的球颜色相同的结果数,然后根据概率公式求解.
【详解】(1)解:由题可得,当n很大时,摸到白球的频率接近0.5;
故答案为:0.5;
(2)∵摸到白球的概率为0.5,
∴估计口袋中白球的个数 (个) .
(3)解:根据题意列表如下:
第二次 第一次 | 白1 | 白2 | 黑1 | 黑2 |
白1 |
| (白1,白2) | (白1,黑1) | (白1,黑2) |
白2 | (白2,白1) |
| (白2,黑1) | (白2,黑2) |
黑1 | (黑1,白1) | (黑1,白2) |
| (黑1,黑2) |
黑2 | (黑2,白1) | (黑2,白2) | (黑2,黑1) |
|
由上表可知,共有12种等可能出现的结果,其中两次摸到的球颜色相同的有4种,分别为:(白1,白2),(白2,白1),(黑2, 黑1),(黑1,黑2),
∴(颜色相同).
【点睛】本题考查了列表法与树状图法以及利用频率估计概率:大量重复实验时,事件发生的频率在某个固定位置左右摆动,并且摆动的幅度越来越小,根据这个频率稳定性定理,可以用频率的集中趋势来估计概率,这个固定的近似值就是这个事件的概率,掌握上述内容是解题的关键.
20.最早再过2小时能侦察到.
【分析】设侦察船由B出发到侦察到这艘军舰经过的时间是x小时,由题中信息可以知道军船和侦察船的行使方向互相垂直,所以军船和侦察船的距离和时间的关系式是:s2=(90−30x)2+(20x)2,s≤50时侦察船可侦察到这艘军舰,所以可以将s=50代入关系式:s2=(90−30x)2+(20x)2求时间x.
【详解】解:能.设侦察船最早由B出发经过x小时侦察到军舰,
则
两边平方得:
整理得
解得:
∵2 <
∴ 最早再过2小时能侦察到.
【点睛】本题考查了一元二次方程的应用,解题的关键是能找出军船和侦察船的距离关系,利用勾股定理正确列出一元二次方程.
21. 每张贺年卡应降价0.1元
【分析】由题意可知:(原来每张贺年卡盈利-降价的价格)×(原来售出的张数+增加的张数)=180,把相关数值代入求解即可.
【详解】解:设每张贺年卡应降价x元,现在的利润是(0.3﹣x)元,则商城多售出200x÷0.05=4000x张.
(0.3﹣x)(500+4000x)=180,
整理得400x2﹣70x+3=0,
(40x﹣3)(10x﹣1)=0,
解得x1=,x2=0.1,
∵为了尽快减少库存,
∴x=0.1.
答:每张贺年卡应降价0.1元.
【点睛】本题考查一元二次方程的应用;得到每降价x元多卖出的贺年卡张数是解决本题的难点;根据利润得到相应的等量关系是解决本题的关键.
22.(1)轮船会进入台风影响区;(2)经过大约轮船就会进入台风影响区
【分析】(1)对比台风中心到达A点时,C与台风中心的距离即可;
(2)设时间为未知数,并求解轮船与台风中心距离等于200km时的时间.
【详解】(1)当台风中心到达A时:
此时轮船距A:
所以轮船不改变航向,会进入台风影响区.
(2)如图所示
设x小时后,轮船就进入台风影响区,根据题意可以:
(千米),(千米)
∵ ,
∴
∴
∴
解得:(舍)
∴轮船经过h就进入台风影响区域.
【点睛】本题主要考查勾股定理的知识,根据勾股定理列方程准确求解是解题的关键.
2023-2024学年广东省深圳市南山区华侨城中学九年级(上)月考数学试卷(12月份)(含解析): 这是一份2023-2024学年广东省深圳市南山区华侨城中学九年级(上)月考数学试卷(12月份)(含解析),共24页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
2023-2024学年广东省深圳市南山区华侨城中学九年级(上)月考数学试卷(12月份)(含解析): 这是一份2023-2024学年广东省深圳市南山区华侨城中学九年级(上)月考数学试卷(12月份)(含解析),共24页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
2023-2024学年广东省深圳市南山区深圳市深中南山创新学校九年级上册月考数学试题(含解析): 这是一份2023-2024学年广东省深圳市南山区深圳市深中南山创新学校九年级上册月考数学试题(含解析),共29页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。












