新高考数学一轮复习知识点总结与题型精练专题22 直线与圆（含解析）

这是一份新高考数学一轮复习知识点总结与题型精练专题22 直线与圆（含解析），共25页。

专题22 直线与圆
【考纲要求】
1、理解直线的斜率和倾斜角的概念，理解直线倾斜角的唯一性及直线斜率的存在性.
2、理解并掌握两条直线平行的条件及两条直线垂直的条件，能根据已知条件判断两直线的平行与垂直.
3、能用解方程组的方法求两直线的交点坐标，会根据方程组解的个数判定两条直线的位置关系．
4、能根据所给条件求圆的标准方程，会用圆心到直线的距离来判断直线与圆的位置关系．
一、直线的倾斜角与斜率
【思维导图】

【考点总结】
1、直线的倾斜角
(1)倾斜角的定义
①当直线l与x轴相交时，取x轴作为基准，x轴正向与直线l向上方向之间所成的角α叫做直线l的倾斜角．
②当直线l与x轴平行或重合时，规定它的倾斜角为0°.
(2)直线的倾斜角α的取值范围为0°≤α<180°.
(3)确定平面直角坐标系中一条直线位置的几何要素是：直线上的一个定点以及它的倾斜角，二者缺一不可．
2、直线的斜率与倾斜角的关系
(1)直线的斜率
把一条直线的倾斜角α的正切值叫做这条直线的斜率，斜率常用小写字母k表示，即k＝tan α.
(2)斜率与倾斜角的对应关系
图示




倾斜角(范围)
α＝0°
0°<α<90°
α＝90°
90°<α<180°
斜率(范围)
k＝0
k>0
不存在
k<0
3、过两点的直线的斜率公式
直线过两点P1(x1，y1)，P2(x2，y2)，其斜率k＝(x1≠x2)．
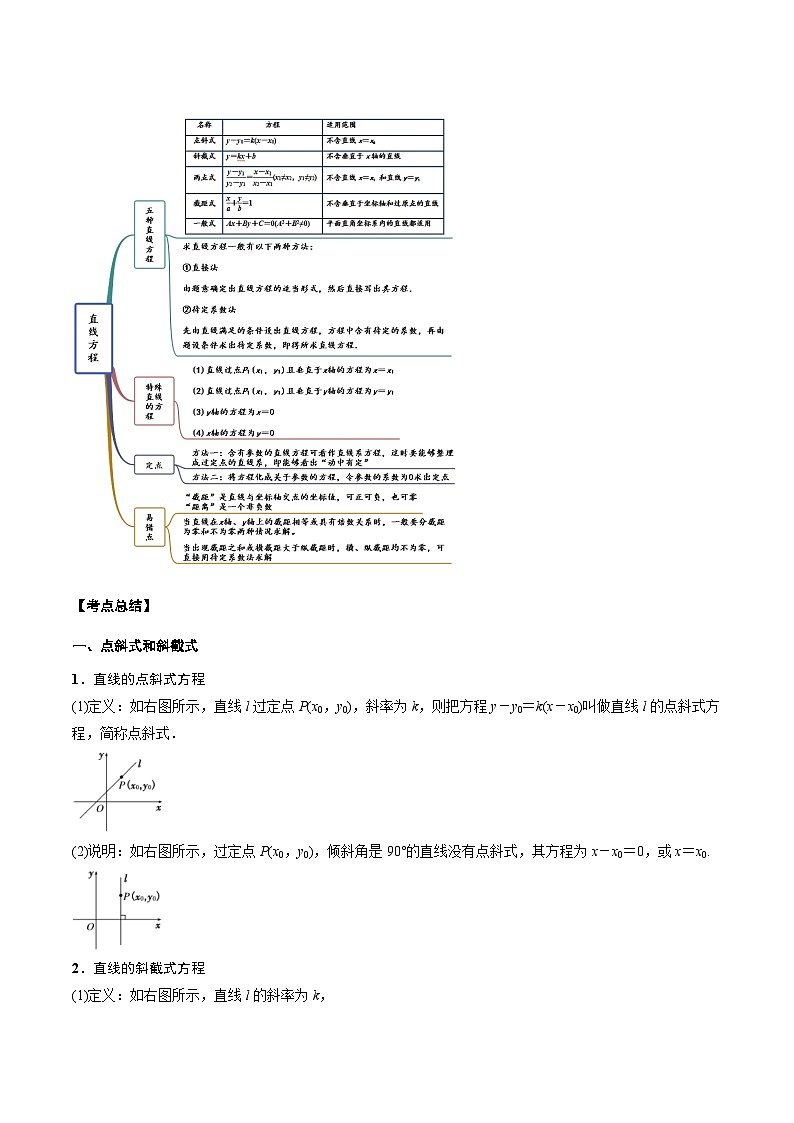
二、直线的方程
【思维导图】

【考点总结】
一、点斜式和斜截式
1．直线的点斜式方程
(1)定义：如右图所示，直线l过定点P(x0，y0)，斜率为k，则把方程y－y0＝k(x－x0)叫做直线l的点斜式方程，简称点斜式．

(2)说明：如右图所示，过定点P(x0，y0)，倾斜角是90°的直线没有点斜式，其方程为x－x0＝0，或x＝x0.

2．直线的斜截式方程
(1)定义：如右图所示，直线l的斜率为k，

且与y轴的交点为(0，b)，则方程y＝kx＋b叫做直线l的斜截式方程，简称斜截式．
(2)说明：一条直线与y轴的交点(0，b)的纵坐标b叫做直线在y轴上的截距．倾斜角是直角的直线没有斜截式方程．
二、两点式和截距式
项目
两点式
截距式
条件
P1(x1，y1)和P2(x2，y2)，其中x1≠x2，y1≠y2
在x轴上截距a，在y轴上截距b
图形


方程
＝
＋＝1
适用范围
不表示垂直于坐标轴的直线
不表示垂直于坐标轴的直线及过原点的直线
三、两条直线的交点坐标两点间的距离
【思维导图】

【考点总结】
一、两条直线的交点坐标
1．两直线的交点坐标
几何元素及关系
代数表示
点A
A(a，b)
直线l
l：Ax＋By＋C＝0
点A在直线l上
Aa＋Bb＋C＝0
直线l1与l2的交点是A
方程组的解是
2．两直线的位置关系
方程组的解
一组
无数组
无解
直线l1与l2的公共点个数
一个
无数个
零个
直线l1与l2的位置关系
相交
重合
平行
二、两点间的距离
两点间的距离公式
(1)公式：点P1(x1，y1)，P2(x2，y2)间的距离公式|P1P2|＝.
(2)文字叙述：平面内两点的距离等于这两点的横坐标之差与纵坐标之差的平方和的算术平方根．
三、点到直线的距离和两条平行直线间的距离
点到直线的距离与两条平行直线间的距离
项目
点到直线的距离
两条平行直线间的距离
定义
点到直线的垂线段的长度
夹在两条平行直线间公垂线段的长度
公式
点P0(x0，y0)到直线l：Ax＋By＋C＝0的距离d＝
两条平行直线l1：Ax＋By＋C1＝0与l2：Ax＋By＋C2＝0(C1≠C2)之间的距离d＝
四、圆的标准方程
【思维导图】

【考点总结】
一、圆的标准方程
几种特殊位置的圆的标准方程：
条件
圆的标准方程
过原点
(x－a)2＋(y－b)2＝a2＋b2(a2＋b2＞0)
圆心在x轴上
(x－a)2＋y2＝r2(r≠0)
圆心在y轴上
x2＋(y－b)2＝r2(r≠0)
圆心在x轴上且过原点
(x－a)2＋y2＝a2(a≠0)
圆心在y轴上且过原点
x2＋(y－b)2＝b2(b≠0)
与x轴相切
(x－a)2＋(y－b)2＝b2(b≠0)
与y轴相切
(x－a)2＋(y－b)2＝a2(a≠0)
二、点与圆的位置关系
圆的标准方程为(x－a)2＋(y－b)2＝r2，圆心C(a，b)，半径为r.设所给点为M(x0，y0)，则
位置关系
判断方法
几何法
代数法
点在圆上
│MC│＝r⇔点M在圆C上
点M(x0，y0)在圆上⇔(x0－a)2＋(y0－b)2＝r2
点在圆内
│MC│ 点M(x0，y0)在圆内⇔(x0－a)2＋(y0－b)2＜r2
点在圆外
│MC│>r⇔点M在圆C外
点M(x0，y0)在圆外⇔(x0－a)2＋(y0－b)2＞r2
【题型汇编】
题型一：直线的倾斜角与斜率
题型二：直线的方程
题型三：直线的交点坐标与距离
题型四：圆的方程
题型五：直线与圆的位置关系
【题型讲解】
题型一：直线的倾斜角与斜率
一、单选题
1．（2022·山东潍坊·二模）已知直线，，若，则(       )
A． B． C．3 D．－3
【答案】A
【解析】
【分析】
两直线斜率均存在时，两直线垂直，斜率相乘等于－1，据此即可列式求出a的值．
【详解】
∵，∴．
故选：A．
2．（2022·浙江台州·二模）已知直线：，：，若，则实数的值为（       ）
A． B． C． D．
【答案】C
【解析】
【分析】
利用一般式下两直线垂直的充要条件“”即可求解
【详解】

故选：C
3．（2022·北京·潞河中学三模）设，若直线与直线平行，则的值是（       ）
A．1 B． C．0 D．0，1
【答案】A
【解析】
【分析】
根据两直线平行则两直线斜率相等截距不相等可得答案.
【详解】
时，两直线为、直线，显然不平行；
所以，两直线为，，
所以，且，
解得．
故选：A.
4．（2022·江西南昌·二模（文））已知直线与直线垂直，则m=（       ）
A．-2 B． C．2 D．
【答案】C
【解析】
【分析】
根据两直线垂直，直接列出方程求解，即可得出结果.
【详解】
当时，，
由知，斜率为2，
所以直线与不垂直，不符合题意；
当时，，
因为直线与直线垂直，
所以，解得.
故选：C.
二、多选题
1．（2022·湖南省临澧县第一中学一模）下列说法正确的是（       ）
A．已知直线与平行，则k的值是3
B．直线与圆的位置关系为相交
C．圆上到直线的距离为的点共有3个
D．已知AC、BD为圆的两条相互垂直的弦，垂足为，则四边形ABCD的面积的最大值为10
【答案】BC
【解析】
【分析】
A由直线平行的判定求参数，注意验证是否重合；B根据直线所过的定点与圆的位置关系判断即可；C由圆心到直线的距离与半径的关系即可判断；D设圆心到的距离分别为，则及，结合基本不等式求最大值即可判断.
【详解】
A：由平行知：，则或，当时有，满足题设，当时有，满足题设，故或，错误；
B：由过定点，而在圆内，故它们的关系为相交，正确；
C：由题设知：圆的标准方程为，则圆心为，半径为，所以圆心到距离为，易知圆上点到直线距离为的点共有3个，正确；
D：设圆心到的距离分别为，则，又相互垂直，所以，而，即当且仅当时等号成立，故，故错误.
故选：BC
题型二：直线的方程
1．（2022·北京市第十二中学三模）已知直线l过圆的圆心，且与直线2x＋y－3＝0垂直，则l的方程为（       ）
A．x－2y＋1＝0 B．x＋2y－1＝0
C．2x＋y－2＝0 D．x－2y－1＝0
【答案】D
【解析】
【分析】
利用配方法求出圆心坐标，结合垂直直线之间斜率的关系进行求解即可.
【详解】
由，所以圆心坐标为，
因为直线2x＋y－3＝0的斜率为，
所以与直线2x＋y－3＝0垂直的直线l的斜率为，
所以l的方程为：，
故选：D
2．（2022·北京工业大学附属中学三模）已知直线，，若，则实数的值是（       ）
A．或 B．或
C． D．
【答案】A
【解析】
【分析】
利用直线的一般式方程，根据直线垂直的条件列出等式，求得答案.
【详解】
由题意可知,故，
解得或，经验证，符合题意，
故选：A
3．（2022·江西·上饶市第一中学二模（文））若经过点的直线与圆相切，则该直线在y轴上的截距为(       )
A． B．5 C． D．
【答案】C
【解析】
【分析】
判断P点在圆上，圆心为原点O，则切线斜率为，根据直线方程的点斜式写出切线方程，令x＝0即可求出它在y轴上的截距.
【详解】
∵，∴P在圆上，
设圆心为O，则，则过P的切线斜率，
∴切线方程为：，
令得.
故选：C.
4．（2022·贵州毕节·三模（理））曲线与直线有两个交点，则实数的取值范围为（       ）
A． B． C． D．
【答案】D
【解析】
【分析】
根据直线过定点的求法可求得直线恒过；由曲线方程可确定图形，采用数形结合的方式可确定直线斜率的取值范围，由此可构造不等式求得的取值范围.
【详解】
由得：，
令，解得：，直线恒过定点；
由得：，
由此可得曲线的图形如下图所示，

由图形可知：当直线过点时，直线斜率为，
若直线与曲线有两个不同交点，则直线斜率的取值范围为，
即，解得：，即实数的取值范围为.
故选：D.
二、多选题
1．（2022·重庆·二模）已知直线，圆，则下列结论正确的是（       ）
A．直线l恒过定点
B．直线l与圆C恒有两个公共点
C．直线l与圆C的相交弦长的最大值为
D．当时，圆C与圆关于直线l对称
【答案】ABD
【解析】
【分析】
将直线方程变形为即可判断直线过定点，进而判断A；再根据定点在圆内判断B；根据直线与圆相交时，最大弦为直径判断C；根据点关于直线的对称性求解关于对称的点坐标，进而求解对称圆的方程判断D.
【详解】
解：对于A选项，因为直线可变形为，所以直线恒过定点，故A选项正确；
对于B选项，因为，所以点在圆内，故直线与圆相交，由两个公共点，故B选项正确；
对于C选项，对于圆，圆心为，半径为，当直线线与圆相交，故相交弦长的最大值为圆的直径，即为，故C选项错误；
对于D选项，当时，直线，故圆的圆心关于对称的点的坐标为 ，所以圆关于对称的圆的方程为，故D选项正确.
故选：ABD
题型三：直线的交点坐标与距离
1．（2022·重庆·三模）已知直线上存在一点P，满足，其中O为坐标原点.则实数k的取值范围是（       ）
A． B． C． D．
【答案】C
【解析】
【分析】
由已知可得原点O到直线l的距离的最大值为1，利用点到直线的距离公式可得关于k的不等式，即可求解k的范围.
【详解】
因为直线上存在一点P，使得，
所以原点O到直线l的距离的最大值为1，即，解得：，
即k的取值范围是.
故选：C
2．（2022·贵州遵义·三模（文））圆O：上点P到直线l：距离的最小值为（       ）
A． B．
C．2 D．0
【答案】B
【解析】
【分析】
根据圆与直线的位置关系，以及点到直线的距离公式即可求解.
【详解】
圆心到直线的距离设为，则，
又因为圆的半径，所以点P到直线l：距离的最小值为
故选：B
3．（2022·甘肃兰州·一模（理））圆的圆心到直线的距离是（       ）
A． B． C．1 D．
【答案】D
【解析】
【分析】
根据已知条件把圆的一般方程转化为标准方程，从而可得到圆心坐标，再代入点到直线的距离公式即可.
【详解】
由题意可得：圆的一般方程为，
转化为标准方程：，
即圆的圆心坐标为，
因为直线方程为，
所以圆心到直线的距离为
故选：D
4．（2022·贵州贵阳·二模（理））已知直线和与圆都相切，则圆的面积的最大值是（       ）
A． B． C． D．
【答案】A
【解析】
【分析】
易得互相平行，故圆的直径为间的距离，再表达出距离求最大值即可得圆的直径最大值，进而得到面积最大值
【详解】
由题，互相平行，且，故圆的直径为间的距离，令，则，，故当，即时取得最大值，此时圆的面积为
故选：A
二、多选题
1．（2022·江苏·海安高级中学二模）已知直线l过点，点，到l的距离相等，则l的方程可能是(       )
A． B．
C． D．
【答案】BC
【解析】
【分析】
分直线l斜率存在和不存在进行讨论﹒当l斜率存在时，设其方程为，根据点到直线的距离公式列出关于k的方程，解方程即可求直线l的方程．
【详解】
当直线的斜率不存在时，直线l的方程为，此时点到直线的距离为5，点到直线的距离为1，此时不成立；
当直线l的斜率存在时，设直线的方程为，即，
∵点到直线的距离相等，
，解得，或，
当时，直线的方程为，整理得，
当时，直线的方程为，整理得
综上，直线的方程可能为或
故选：BC．
题型四：圆的方程
一、单选题
1．（2022·北京·高考真题）若直线是圆的一条对称轴，则（       ）
A． B． C．1 D．
【答案】A
【解析】
【分析】
若直线是圆的对称轴，则直线过圆心，将圆心代入直线计算求解．
【详解】
由题可知圆心为，因为直线是圆的对称轴，所以圆心在直线上，即，解得．
故选：A．
2．（2022·北京丰台·一模）已知圆，则圆心到直线的距离等于（       ）
A． B． C． D．
【答案】C
【解析】
【分析】
求出圆心的坐标，即可求得圆心到直线的距离.
【详解】
圆的标准方程为，圆心为，故圆心到直线的距离为.
故选：C.
3．（2022·广西南宁·二模（文））已知圆，圆，过动点P分别作圆、圆的切线PA，PB（A，B为切点），使得，则动点P的轨迹方程为（       ）．
A． B．
C． D．
【答案】D
【解析】
【分析】
由条件结合圆的切线性质可得出，结合两点间的距离公式可得出答案.
【详解】
由得．
因为两圆的半径均为1，则，
则，即．
所以点P的轨迹方程为．
故选：D
4．（2022·安徽滁州·二模（文））已知A，B为圆上的两个动点，P为弦的中点，若，则点P的轨迹方程为（）
A． B．
C． D．
【答案】B
【解析】
【分析】
在直角三角形中利用几何关系即可获解
【详解】
圆即,半径
因为,所以
又是的中点,所以
所以点的轨迹方程为
故选：B

二、多选题
1．（2022·江苏南京·三模）在平面直角坐标系中，已知圆：，则下列说法正确的是（       ）
A．若，则点在圆外
B．圆与轴相切
C．若圆截轴所得弦长为，则
D．点到圆上一点的最大距离和最小距离的乘积为
【答案】ABD
【解析】
【分析】
选项A，根据点与圆的位置关系判断即可；选项B，根据直线与圆相切的定义判断即可；选项C，根据圆的弦长公式求解即可；选项D，根据分和两种情况即可判断.
【详解】
对于A，因为时，将原点代入圆方程可得，故点在圆外，故A正确；
对于B，圆化为标准方程即为，则圆心，，
显然圆心到轴距离为等于半径，所以相切，故B正确；
对于C，对根据题意，，解得，解得所以圆截轴所得弦长为，
则，故C不正确；
对于D，当时，圆：，所以点在圆上，显然最小值为，最大值为，
故乘积且等于；当时，由选项A知，点在圆外，，
所以最大值为，最小值为，乘积为，故D正确.
故选：ABD.
题型五：直线与圆的位置关系
一、单选题
1．（2022·江西萍乡·三模（文））已知直线被圆截得的弦长为2，则（       ）
A． B． C．3 D．4
【答案】A
【解析】
【分析】
根据半径的平方等于弦长一半的平方加圆心到直线的距离的平方，即可求出答案.
【详解】
圆心到直线的距离，弦长的一半为1，.
故选：A.
2．（2022·广东佛山·三模）已知集合，，则的元素个数是（       ）
A．0 B．1 C．2 D．4
【答案】C
【解析】
【分析】
依据直线与圆的位置关系去判断的元素个数
【详解】
集合表示以为圆心2为半径的圆上的所有点
集合表示直线上的所有点
圆心到直线的距离，
则直线与圆相交，有两个公共点，
则的元素个数为2
故选：C
3．（2022·安徽淮北·一模（理））直线与圆的位置关系是（       ）
A．相离 B．相交 C．相切 D．不确定
【答案】B
【解析】
【分析】
直线与圆的位置关系的判断，第一步求出圆的圆心及半径，第二步求出圆心到直线的距离，距离大于半径相离，等于半径相切，小于半径相交.
【详解】
圆的圆心坐标为 半径为4，圆心到直线的距离，所以相交.
故选：B.
4．（2022·河南·一模（文））若点为圆的弦的中点，则弦所在直线方程为（       ）
A． B．
C． D．
【答案】D
【解析】
【分析】
若圆心为，则可求的斜率，由过即可写出弦所在直线方程.
【详解】
由题意，由圆心且，而，
∴，直线过，则所在直线方程为，
∴整理得：.
故选：D.
5．（2022·山东济南·三模）已知圆：，若圆与轴交于，两点，且，则（       ）
A． B．2 C． D．1
【答案】B
【解析】
【分析】
根据题意设，，由垂径定理得，，求解即可.
【详解】
：的圆心，半径为，圆心到直线的距离为，
因为圆与轴交于，两点，且，所以设，，
由垂径定理得，，即，解得，所以.
故选：B.
6．（2022·辽宁·东北育才学校二模）关于圆，有下列四个命题：甲：圆的半径；乙：直线与圆相切；丙：圆经过点；丁：直线平分圆，如果只有一个命题是假命题，则该命题是（       ）
A．甲 B．乙 C．丙 D．丁
【答案】B
【解析】
【分析】
根据命题为真时，分别解得乙丙丁命题中的参数a的值，结合题意，如果只有一个命题是假命题，即可判断哪个命题为假命题.
【详解】
圆的圆心为 ，半径为 ，
甲：圆的半径；
当乙为真命题时，则 ，解得 或 ，
则 或3；
当丙为真命题时，，解得 ，
则圆的半径为1；
当丁为真命题时，直线平分圆，则直线过圆心，
即 ，
则圆的半径为1；
故四个命题中只有一个命题是假命题时，只能是乙，
故选：B
二、多选题
1．（2022·辽宁鞍山·二模）已知M为圆C：上的动点，P为直线l：上的动点，则下列结论正确的是（       ）
A．直线l与圆C相切 B．直线l与圆C相离
C．|PM|的最大值为 D．|PM|的最小值为
【答案】BD
【解析】
【分析】
根据圆心到直线l得距离，可知直线l与圆C相离；
∵P、M均为动点，对|PM|先固定点P可得，再看不难发现，
即．
【详解】
圆C：得圆心,半径
∵圆心到直线l：得距离
∴直线l与圆C相离
A不正确，B正确；

C不正确，D正确；
故选：BD．
2．（2022·广东广州·一模）已知直线与圆，则（       ）
A．直线与圆C相离
B．直线与圆C相交
C．圆C上到直线的距离为1的点共有2个
D．圆C上到直线的距离为1的点共有3个
【答案】BD
【解析】
【分析】
根据直线与圆的位置关系可判断.
【详解】
由圆，可知其圆心坐标为，半径为，
圆心到直线的距离，所以可知选项B，D正确，选项A，C错误.
故选：BD
3．（2022·广东汕头·三模）关于曲线C：，下列说法正确的是（       ）
A．曲线C一定不过点
B．若，过原点与曲线C相切的直线有两条
C．若，曲线C表示两条直线
D．若，则直线被曲线C截得弦长等于
【答案】AB
【解析】
【分析】
直接将点代入曲线C方程，由方程无解即可判断A选项；先由原点到圆心的距离判断出原点在圆外即可判断B选项；代入曲线C解出即可判断C选项；先求出圆心在直线上结合直径即可判断D选项
【详解】
将点代入曲线C：可得，整理得，
即，显然此方程无解，即曲线C一定不过点，A正确；
时，易得曲线C是圆心为，半径为的圆，此时原点和圆心之间的距离为，
，故原点在圆外，过原点有两条直线与曲线C相切，B正确；
时，曲线C：，则，解得，则曲线C表示一个点，C错误；
时，曲线C：，圆心在直线上，则直线被曲线C截得弦长即为圆的直径等于2，D错误.
故选：AB.