

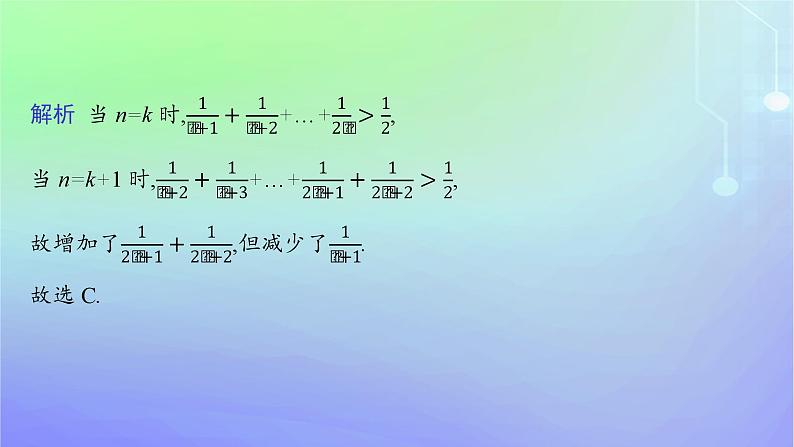





- 新教材2023_2024学年高中数学第一章数列3等比数列3.2等比数列的前n项和第二课时等比数列前n项和的综合应用分层作业课件北师大版选择性必修第二册 课件 0 次下载
- 新教材2023_2024学年高中数学第一章数列4数列在日常经济生活中的应用分层作业课件北师大版选择性必修第二册 课件 0 次下载
- 新教材2023_2024学年高中数学第一章数列培优课1数列的通项公式问题分层作业课件北师大版选择性必修第二册 课件 0 次下载
- 新教材2023_2024学年高中数学第一章数列培优课2数列的求和问题分层作业课件北师大版选择性必修第二册 课件 0 次下载
- 新教材2023_2024学年高中数学第一章数列综合训练课件北师大版选择性必修第二册 课件 0 次下载
数学选择性必修 第二册第一章 数列5 数学归纳法作业ppt课件
展开2.[2023北京八中校考期中]在用数学归纳法证明(n+1)·(n+2)…(n+n)=2n·1·3·5·…·(2n-1)(n∈N+)的过程中,从“k到k+1”左边需增乘的代数式为( )A.2k+2B.(2k+1)(2k+2)D.2(2k+1)
解析 当n=k时,左边A=(k+1)(k+2)…(k+k)=(k+1)(k+2)…2k,当n=k+1时,左边B=(k+2)(k+3)…(k+1+k+1)=(k+2)(k+3)…(2k+2),故选D.
3.已知数列{an}满足an+1an-2n2(an+1-an)+1=0,且a1=1,其前n项和为Sn,则S15=( )A.196B.225C.256D.289
解析 因为a1=1,故a2-2×(a2-1)+1=0,故a2=3,同理a3=5,猜想an=2n-1,下面用数学归纳法证明an=2n-1.当n=1时,a1=2×1-1=1,设当n=k时,ak=2k-1,则当n=k+1时,有(2k-1)ak+1-2k2(ak+1-2k+1)+1=0,故ak+1=2k+1=2(k+1)-1,故由数学归纳法可得an=2n-1.
5.用数学归纳法证明不等式2n>(n+1)2(n∈N+)时,初始值n0应等于 .
解析 由题意,当n=1时,21<(1+1)2;当n=2时,22<(2+1)2;当n=3时,23<(3+1)2;当n=4时,24<(4+1)2;当n=5时,25<(5+1)2;当n=6时,26>(6+1)2,所以用数学归纳法证明不等式2n>(n+1)2(n∈N+)时,初始值n0应等于6.
6.用数学归纳法证明 .假设n=k时,不等式成立,则当n=k+1时,应推证的目标不等式是 .
7.已知数列{an}满足Sn+an=n.(1)写出a1,a2,a3,并猜想数列{an}的通项公式;(2)用数学归纳法证明数列{an}的通项公式.
8.(多选题)在数学上,斐波那契数列{an}可以用递推的方法来定义a1=1,a2=1,an+2=an+1+an(n∈N+),则( )A.a1+a3+a5+…+a2 021=a2 022B.a1+a2+a3+…+a2 020=a2 022
解析 对于A,由an+2=an+1+an,可得an+1=an+2-an,则a3=a4-a2,a5=a6-a4,a7=a8-a6,…,a2 021=a2 022-a2 020,将上式累加得a3+a5+a7+…+a2 021=a2 022-a2,又因为a1=a2=1,则有a1+a3+…+a2 021=a2 022.故A正确;对于B,由an+2=an+1+an,可得a3=a2+a1,a4=a3+a2,…,a2 022=a2 021+a2 020,将上式累加得a2 022=a2+(a1+a2+a3+…+a2 020),又因为a2=1,则a1+a2+a3+…+a2 020=a2 022-1,故B错误;
则下列说法错误的是( )A.过程全部正确B.n=1的验证不正确C.n=k的归纳假设不正确D.从n=k到n=k+1的推理不正确
解析 当n=k+1时,没有应用当n=k时的假设,即从n=k到n=k+1的推理不正确.故选ABC.
11.(多选题)设f(x)是定义在正整数集上的函数,且f(x)满足:当f(k)≥k+1成立时,总有f(k+1)≥k+2成立.下列命题总成立的是( )A.若f(6)<7成立,则f(5)<6成立B.若f(3)≥4成立,则当k≥1时,均有f(k)≥k+1成立C.若f(2)<3成立,则f(1)≥2成立D.若f(4)≥5成立,则当k≥4时,均有f(k)≥k+1成立
解析 若f(5)<6不成立,则f(5)≥6,由题意知f(6)≥7,与f(6)<7成立矛盾,所以f(5)<6成立,A正确.B,C显然错误.若f(4)≥5成立,由题意,得当k≥4时,均有f(k)≥k+1成立,故D正确.所以选AD.
12.在用数学归纳法证明“f(n)= <1(n∈N+,n≥3)”的过程中,假设当n=k(k∈N+,k≥3)时,不等式f(k)<1成立,当证明n=k+1,f(k+1)<1也成立时,若f(k+1)=f(k)+g(k),则g(k)= .
13.试比较2n+2与n2的大小(n∈N+),并用数学归纳法证明你的结论.
解 当n=1时,21+2=4>n2=1,当n=2时,22+2=6>n2=4,当n=3时,23+2=10>n2=9,当n=4时,24+2=18>n2=16,由此可以猜想,2n+2>n2(n∈N+)成立.下面用数学归纳法证明:(1)当n=1时,21+2>12,所以原不等式成立.当n=2时,22+2>22,所以原不等式成立.当n=3时,23+2>32,所以原不等式成立.
(2)假设当n=k时(k≥3且k∈N+)时,不等式成立,即2k+2>k2.当n=k+1时,2k+1+2=2×2k+2=2(2k+2)-2>2k2-2.又2k2-2-(k+1)2=k2-2k-3=(k-3)(k+1)≥0,即2k2-2≥(k+1)2,故2k+1+2>(k+1)2成立.根据(1)和(2),原不等式对于任意n∈N+都成立.
14.已知数列{an}的前n项和为Sn,且 -(an+2)Sn+1=0.(1)求S1,S2,S3,并猜想Sn(n∈N+);(2)用数学归纳法证明你的猜想.
15.汉诺塔问题源于一种古老的益智游戏.这个游戏的目的是将图1中按照直径从小到大依次摆放在①号塔座上的盘子,移动到③号塔座上,在移动的过程中要求:每次只可以移动一个盘子,并且保证任何一个盘子都不可以放在比自己小的盘子上.记将n个直径不同的盘子从①号塔座移动到③号塔座所需要的最少次数为an.
(1)试写出a1,a2,a3,a4的值,并猜想出an.(2)著名的毕达哥拉斯学派提出了形数的概念.他们利用小石子摆放出了图2的形状,此时小石子的数目分别为1,4,9,16,由于小石子围成的图形类似正方形,于是称bn=n2这样的数为正方形数.当n≥2时,试比较an与bn的大小,并用数学归纳法加以证明.
解 (1)由题意得,a1=1,a2=3,a3=7,a4=15,猜想an=2n-1.(2)a1=1,a2=3,a3=7,a4=15,a5=31,b1=1,b2=4,b3=9,b4=16,b5=25.则当2≤n<5时,an
高中数学北师大版 (2019)选择性必修 第二册第一章 数列5 数学归纳法课文配套ppt课件: 这是一份高中数学北师大版 (2019)选择性必修 第二册第一章 数列5 数学归纳法课文配套ppt课件,共40页。PPT课件主要包含了§5数学归纳法,素养目标•定方向,必备知识•探新知,n=k+1,关键能力•攻重难,题型探究,易错警示,课堂检测•固双基等内容,欢迎下载使用。
北师大版 (2019)选择性必修 第二册5 数学归纳法评课课件ppt: 这是一份北师大版 (2019)选择性必修 第二册5 数学归纳法评课课件ppt,共31页。PPT课件主要包含了目录索引,本节要点归纳等内容,欢迎下载使用。
高中数学北师大版 (2019)选择性必修 第二册4 数列在日常经济生活中的应用作业课件ppt: 这是一份高中数学北师大版 (2019)选择性必修 第二册4 数列在日常经济生活中的应用作业课件ppt,共40页。













