精品解析：广东省深圳市龙岗区2022--2023学年九年级上学期阶段性训练数学试卷

深圳市龙岗区2022—2023学年第一学期阶段性训练九年级数学试卷

考试时长：90分钟

一、选择题（每小题3分，共30分．在每小题列出的选项中，选出符合题目的一项）

1. 下列方程中，关于x的一元二次方程是（    ）

A. 2x﹣3＝x B. 2x+3y＝5 C. 2x﹣x2＝1 D.

2. 根据下面表格中的对应值：

判断方程ax2＋bx＋c＝0（a≠0，a，b，c为常数）的一个解x的范围是（    ）

A. 3＜x＜3.23 B. 3.23＜x＜3.24

C. 3.24＜x＜3.25 D. 3.25＜x＜3.26

3. 已知是一元二次方程的一个根，则代数式的值为（    ）

A. 2020 B. 2021 C. 2022 D. 2023

4. 已知关于x的一元二次方程有两个不相等的实数根，则a的取值范围是（    ）

A.  B.  C. 且 D. 且

5. 已知不透明的袋中只装有黑、白两种球，这些球除颜色外都相同，其中白球有30个，黑球有n个．随机地从袋中摸出一个球，记录下颜色后，放回袋子中并摇匀，再从中摸出一个球，经过如此大量重复试验，发现摸出的黑球的频率稳定在0.4附近，则n的值约为（    ）

A. 20 B. 30 C. 40 D. 50

6. 下列命题是真命题的是（  ）

A. 对角线相等的四边形是平行四边形

B. 对角线互相平分且相等的四边形是矩形

C. 对角线互相垂直的四边形是菱形

D. 对角线互相垂直平分的四边形是正方形

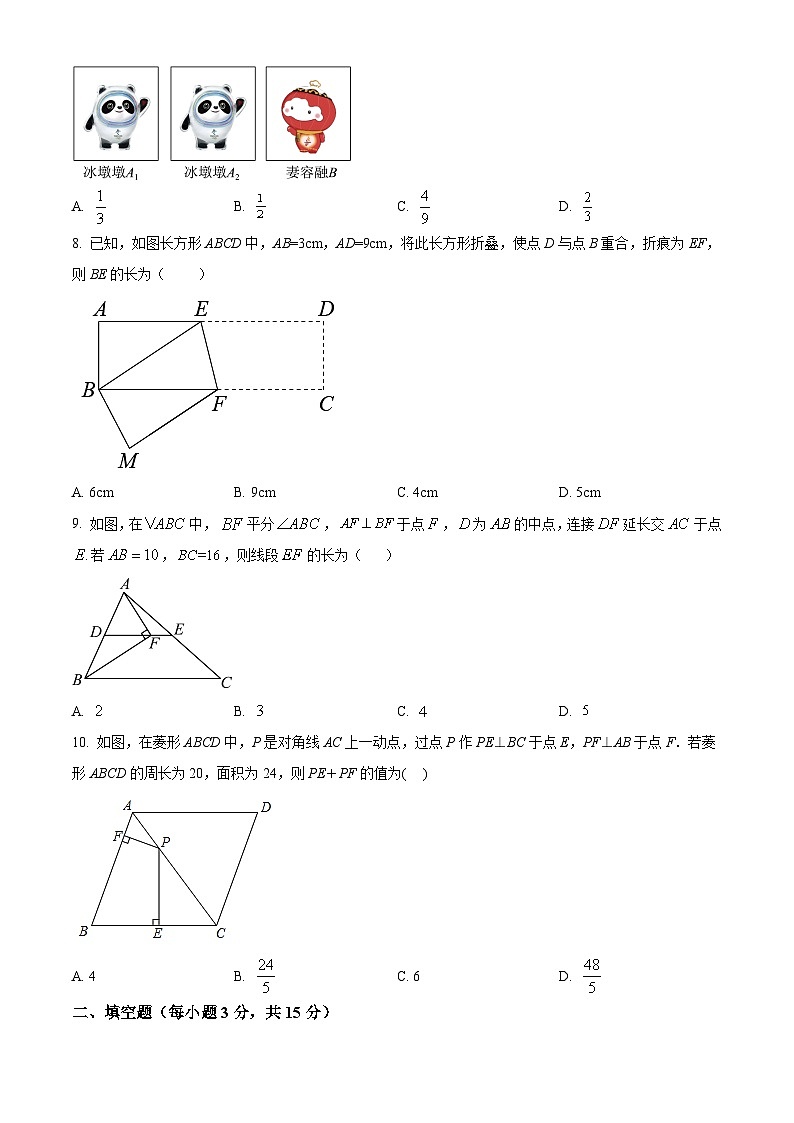
7. 2022年冬奥会吉祥物为“冰墩墩”，冬残奥会吉祥物为“雪容融”．如图，现有三张正面明有吉祥物的不透明卡片，卡片除正两图案不同外，其余均相同，其中两张正面印有冰墩墩图案，一张正面印有雪容融图案，将三张卡片正面向下洗匀，从中随机仙取两张卡片，则抽出的两张都是冰墩墩卡片的概率事（　　）

A.  B.  C.  D.

8. 已知，如图长方形ABCD中，AB=3cm，AD=9cm，将此长方形折叠，使点D与点B重合，折痕为EF，则BE的长为（　 　）

A. 6cm B. 9cm C. 4cm D. 5cm

9. 如图，在中，平分，于点，为的中点，连接延长交于点若，，则线段的长为（    ）

A.  B.  C.  D.

10. 如图，在菱形ABCD中，P是对角线AC上一动点，过点P作PE⊥BC于点E，PF⊥AB于点F．若菱形ABCD的周长为20，面积为24，则PE＋PF的值为(   )

A. 4 B.  C. 6 D.

二、填空题（每小题3分，共15分）

11. 若关于方程的一个根为3，则的值为______．

12. 关于的方程的两根分别为、，则的值为________．

13. 中国古代有着辉煌的数学成就，《周髀算经》、《九章算术》、《海岛算经》、《孙子算经》等是我国古代数学的重要文献.某中学拟从这4部数学名著中选择2部作为“数学文化”校本课程学习内容，恰好选中《九章算术》和《孙子算经》的概率是_______.

14. 如图，在中，，，，是上一点，于点，于点，连接，则的最小值为___________．

15. 如图，在Rt△ABC中，∠C＝90°，AC＝5，以AB为一边向三角形外作正方形ABEF，正方形的中心为O， ，则BC边的长为_．

三、解答题（本大题共7小题，共55分．解答应写出文字说明，证明过程或演算步骤）

16. 解方程：

（1）；

（2）；

（3）；

（4）．

17. 关于x一元二次方程有两个不等实根、．

（1）求实数k的取值范围；

（2）若方程两实根、满足，求k的值．

18. 某单位食堂为全体名职工提供了四种套餐，为了解职工对这四种套餐的喜好情况，单位随机抽取名职工进行“你最喜欢哪一种套餐（必选且只选一种）”问卷调查，根据调查结果绘制了条形统计图和扇形统计图，部分信息如下：

在抽取人中最喜欢套餐的人数为          ，扇形统计图中“”对应扇形的圆心角的大小为          ；

依据本次调查结果，估计全体名职工中最喜欢套餐的人数；

现从甲、乙、丙、丁四名职工中任选两人担任“食品安全监督员”，求甲被选到的概率．

19. 某学校计划利用一片空地建一个学生自行车车棚，其中一面靠墙，这堵墙的长度为12米．计划建造车棚的面积为80平方米，已知现有的木板材料可使新建板墙的总长为26米，

（1）为了方便学生出行，学校决定在与墙平行的一面开一个2米宽的门，那么这个车棚的长和宽分别应为多少米？

（2）如图，为了方便学生取车，施工单位决定在车棚内修建几条等宽的小路，使得停放自行车的面积为54米，那么小路的宽度是多少米？

20. 如图，点是菱形的对角线的交点，，，连接.

（1）求证：；

（2）若四边形的面积是，则菱形的面积是多少.

21. 今年是我国脱贫胜利年，我国在扶贫方面取得了巨大的成就，技术扶贫也使得我省某县的一个电子器件厂脱贫扭亏为盈．该电子器件厂生产一种电脑显卡，2019年该类电脑显卡的出厂价是200元/个，2020年，2021年连续两年在技术扶贫的帮助下改进技术，降低成本，2021年该电脑显卡的出厂价调整为162元/个．

（1）这两年此类电脑显卡出厂价下降的百分率相同，则平均每年下降的百分率是      ；

（2）2021年某赛格电脑城以出厂价购进若干个此类电脑显卡，以200元/个销售时，平均每天可销售20个．为了减少库存，商场决定降价销售．经调查发现，单价每降低5元，每天可多售出10个，如果每天盈利1150元，单价应降低多少元？

22. 已知，如图，为坐标原点，四边形为矩形，，，点是的中点，动点在线段上以每秒个单位长的速度由点向运动．设动点的运动时间为秒．

（1）当为何值时，四边形是平行四边形？

（2）在直线上是否存在一点，使得、、、四点为顶点的四边形是菱形？若存在，求的值，并求出点的坐标；若不存在，请说明理由．

（3）在线段上有一点，且，当运动几秒时，四边形的周长最小，并画图标出点的位置．