

- 新高考数学模拟测试卷06(原卷版+解析版) 试卷 0 次下载
- 新高考数学模拟测试卷05(原卷版+解析版) 试卷 0 次下载
- 新高考数学模拟测试卷04(原卷版+解析版) 试卷 0 次下载
- 新高考数学模拟测试卷02(原卷版+解析版) 试卷 0 次下载
- 新高考数学模拟测试卷01(原卷版+解析版) 试卷 0 次下载
新高考数学模拟测试卷03(原卷版+解析版)
展开1.设集合 SKIPIF 1 < 0 , SKIPIF 1 < 0 ,则 SKIPIF 1 < 0 ( )
A. SKIPIF 1 < 0 B. SKIPIF 1 < 0
C. SKIPIF 1 < 0 D. SKIPIF 1 < 0
2.若复数 SKIPIF 1 < 0 满足 SKIPIF 1 < 0 ,其中 SKIPIF 1 < 0 为虚数单位,则 SKIPIF 1 < 0 的实部为( )
A. SKIPIF 1 < 0 B. SKIPIF 1 < 0 C. SKIPIF 1 < 0 D. SKIPIF 1 < 0
3.已知命题 SKIPIF 1 < 0 SKIPIF 1 < 0 ;命题 SKIPIF 1 < 0 , SKIPIF 1 < 0 .则下列命题中是真命题的为( )
A. SKIPIF 1 < 0 B. SKIPIF 1 < 0 C. SKIPIF 1 < 0 D. SKIPIF 1 < 0
4.本次模拟考试结束后,班级要排一张语文、数学、英语、物理、化学、生物六科试卷讲评顺序表,若化学排在生物前面,数学与物理不相邻且都不排在最后,则不同的排表方法共有( )
A.72种B.144种C.288种D.360种
5.Lgistic模型是常用数学模型之一,可应用于流行病学领域.有学者根据公布数据建立了某地区新冠肺炎累计确诊病例数 SKIPIF 1 < 0 ( SKIPIF 1 < 0 的单位:天)的Lgistic模型: SKIPIF 1 < 0 ,其中 SKIPIF 1 < 0 为最大确诊病例数.当 SKIPIF 1 < 0 时,标志着已初步遏制疫情,则 SKIPIF 1 < 0 约为( )(参考数据: SKIPIF 1 < 0 )
A.60B.62C.66D.63
6.已知正数 SKIPIF 1 < 0 是关于 SKIPIF 1 < 0 的方程 SKIPIF 1 < 0 的两根,则 SKIPIF 1 < 0 的最小值为( )
A.2B. SKIPIF 1 < 0 C.4D. SKIPIF 1 < 0
7.已知双曲线C: SKIPIF 1 < 0 (a>0,b>0)的右焦点为F,点A,B分别为双曲线的左,右顶点,以AB为直径的圆与双曲线C的两条渐近线在第一,二象限分别交于P,Q两点,若OQ∥PF(O为坐标原点),则该双曲线的离心率为( )
A. SKIPIF 1 < 0 B.2C. SKIPIF 1 < 0 D. SKIPIF 1 < 0
8.定义在 SKIPIF 1 < 0 上的函数 SKIPIF 1 < 0 的导函数为 SKIPIF 1 < 0 ,若 SKIPIF 1 < 0 ,则不等式 SKIPIF 1 < 0 的解集是( )
A. SKIPIF 1 < 0 B. SKIPIF 1 < 0 C. SKIPIF 1 < 0 D. SKIPIF 1 < 0
二、选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分.
9.为比较甲、乙两地某月14时的气温状况,随机选取该月中的5天,将这5天中14时的气温数据(单位:℃)制成如图所示的茎叶图.考虑以下结论:其中根据茎叶图能得到的统计结论为( )
A.甲地该月14时的平均气温低于乙地该月14时的平均气温;
B.甲地该月14时的平均气温高于乙地该月14时的平均气温;
C.甲地该月14时的平均气温的标准差小于乙地该月14时的气温的标准差;
D.甲地该月14时的平均气温的标准差大于乙地该月14时的气温的标准差.
10.已知函数 SKIPIF 1 < 0 ,下列结论正确的是( )
A. SKIPIF 1 < 0 的最小正周期为 SKIPIF 1 < 0
B.函数 SKIPIF 1 < 0 的图象关于直线 SKIPIF 1 < 0 对称.
C.函数 SKIPIF 1 < 0 在 SKIPIF 1 < 0 上单调递增
D.方程 SKIPIF 1 < 0 在 SKIPIF 1 < 0 上有 SKIPIF 1 < 0 个不同的实根
11.在数列 SKIPIF 1 < 0 中, SKIPIF 1 < 0 和 SKIPIF 1 < 0 是关于 SKIPIF 1 < 0 的一元二次方程 SKIPIF 1 < 0 的两个根,下列说法正确的是( )
A.实数 SKIPIF 1 < 0 的取值范围是 SKIPIF 1 < 0 或 SKIPIF 1 < 0
B.若数列 SKIPIF 1 < 0 为等差数列,则数列 SKIPIF 1 < 0 的前7项和为 SKIPIF 1 < 0
C.若数列 SKIPIF 1 < 0 为等比数列且 SKIPIF 1 < 0 ,则 SKIPIF 1 < 0
D.若数列 SKIPIF 1 < 0 为等比数列且 SKIPIF 1 < 0 ,则 SKIPIF 1 < 0 的最小值为4
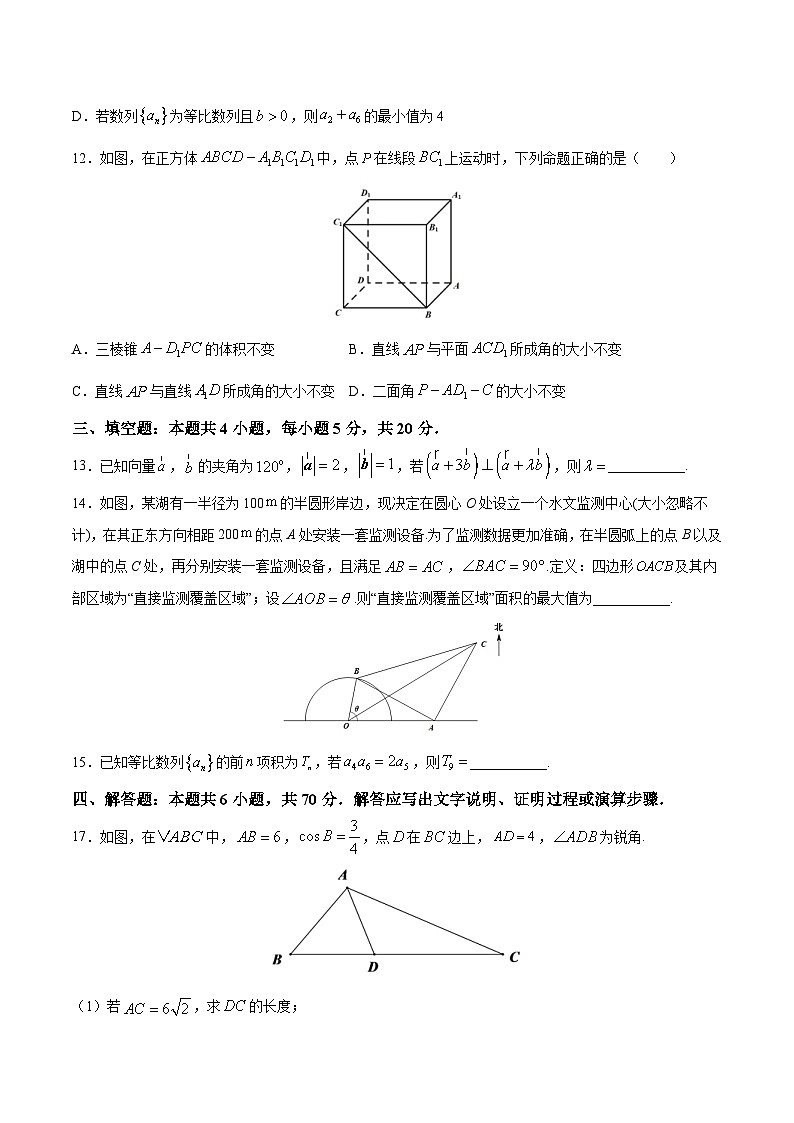
12.如图,在正方体 SKIPIF 1 < 0 中,点 SKIPIF 1 < 0 在线段 SKIPIF 1 < 0 上运动时,下列命题正确的是( )
A.三棱锥 SKIPIF 1 < 0 的体积不变B.直线 SKIPIF 1 < 0 与平面 SKIPIF 1 < 0 所成角的大小不变
C.直线 SKIPIF 1 < 0 与直线 SKIPIF 1 < 0 所成角的大小不变D.二面角 SKIPIF 1 < 0 的大小不变
三、填空题:本题共4小题,每小题5分,共20分.
13.已知向量 SKIPIF 1 < 0 , SKIPIF 1 < 0 的夹角为 SKIPIF 1 < 0 , SKIPIF 1 < 0 , SKIPIF 1 < 0 ,若 SKIPIF 1 < 0 ,则 SKIPIF 1 < 0 ___________.
14.如图,某湖有一半径为100 SKIPIF 1 < 0 的半圆形岸边,现决定在圆心O处设立一个水文监测中心(大小忽略不计),在其正东方向相距200 SKIPIF 1 < 0 的点A处安装一套监测设备.为了监测数据更加准确,在半圆弧上的点B以及湖中的点C处,再分别安装一套监测设备,且满足 SKIPIF 1 < 0 , SKIPIF 1 < 0 .定义:四边形 SKIPIF 1 < 0 及其内部区域为“直接监测覆盖区域”;设 SKIPIF 1 < 0 .则“直接监测覆盖区域”面积的最大值为___________.
15.已知等比数列 SKIPIF 1 < 0 的前 SKIPIF 1 < 0 项积为 SKIPIF 1 < 0 ,若 SKIPIF 1 < 0 ,则 SKIPIF 1 < 0 ___________.
四、解答题:本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.
17.如图,在 SKIPIF 1 < 0 中, SKIPIF 1 < 0 , SKIPIF 1 < 0 ,点 SKIPIF 1 < 0 在 SKIPIF 1 < 0 边上, SKIPIF 1 < 0 , SKIPIF 1 < 0 为锐角.
(1)若 SKIPIF 1 < 0 ,求 SKIPIF 1 < 0 的长度;
(2)若 SKIPIF 1 < 0 ,求 SKIPIF 1 < 0 的值.
18.已知等比数列 SKIPIF 1 < 0 的公比为q.
(1)试问数列 SKIPIF 1 < 0 一定是等比数列吗?说明你的理由;
(2)在① SKIPIF 1 < 0 ,② SKIPIF 1 < 0 ,③ SKIPIF 1 < 0 这三个条件中任选两个,补充在下面的问题中并解答.
问题:若 ,求 SKIPIF 1 < 0 的通项公式及数列 SKIPIF 1 < 0 的前n项和 SKIPIF 1 < 0 .
注:如果选择多种情况解答,则按第一种情况计分.
19.甲、乙两人想参加某项竞赛,根据以往20次的测试分别获得甲、乙测试成绩的频率分布直方图.
已知甲测试成绩的中位数为75.
(1)求 SKIPIF 1 < 0 , SKIPIF 1 < 0 的值,并分别求出甲、乙两人测试成绩的平均数(假设同一组中的每个数据可用该组区间中点值代替).
(2)某学校参加该项竞赛仅有一个名额,结合平时的训练成绩甲、乙两名学生进入最后选拔,学校为此设计了如下选拔方案:答题过程中,若答对则继续答题,若答错则换对方答题例如,若甲首先答题,则他答第1题,若答对继续答第2题如果第2题也答对,继续答第3题,直到他答错则换成乙开始答题,……,直到乙答错再换成甲答题依次类推两人共计答完21道题时答题结束,答对题目数量多者胜出.已知甲、乙两人答对其中每道题的概率都是 SKIPIF 1 < 0 ,假设由以往20次的测试成绩平均分高的同学在选拔比赛中最先开始作答,且记第 SKIPIF 1 < 0 道题也由该同学(最先答题的同学)作答的概率为 SKIPIF 1 < 0 ,其中 SKIPIF 1 < 0
①求 SKIPIF 1 < 0 , SKIPIF 1 < 0 ;
②求证 SKIPIF 1 < 0 为等比数列,并求 SKIPIF 1 < 0 的表达式.
20.如图,在三棱柱 SKIPIF 1 < 0 中,侧面 SKIPIF 1 < 0 为正方形,点 SKIPIF 1 < 0 、 SKIPIF 1 < 0 分别是 SKIPIF 1 < 0 、 SKIPIF 1 < 0 的中点, SKIPIF 1 < 0 平面 SKIPIF 1 < 0 .
(Ⅰ)求证: SKIPIF 1 < 0 平面 SKIPIF 1 < 0 ;
(Ⅱ)若 SKIPIF 1 < 0 是边长为 SKIPIF 1 < 0 的菱形,求直线 SKIPIF 1 < 0 与平面 SKIPIF 1 < 0 所成角的正弦值.
21.设函数 SKIPIF 1 < 0 ,
(I)求函数 SKIPIF 1 < 0 的单调区间;
(Ⅱ)设对于任意 SKIPIF 1 < 0 ,且 SKIPIF 1 < 0 ,都有 SKIPIF 1 < 0 恒成立,求实数 SKIPIF 1 < 0 的取值范围.
22.已知椭圆 SKIPIF 1 < 0 经过点 SKIPIF 1 < 0 ,且右焦点 SKIPIF 1 < 0 .
(1)求椭圆 SKIPIF 1 < 0 的标准方程;
(2)过 SKIPIF 1 < 0 且斜率存在的直线 SKIPIF 1 < 0 交椭圆 SKIPIF 1 < 0 于 SKIPIF 1 < 0 , SKIPIF 1 < 0 两点,记 SKIPIF 1 < 0 ,若 SKIPIF 1 < 0 的最大值和最小值分别为 SKIPIF 1 < 0 , SKIPIF 1 < 0 ,求 SKIPIF 1 < 0 的值.
新高考数学模拟测试卷
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.设集合 SKIPIF 1 < 0 , SKIPIF 1 < 0 ,则 SKIPIF 1 < 0 ( )
A. SKIPIF 1 < 0 B. SKIPIF 1 < 0
C. SKIPIF 1 < 0 D. SKIPIF 1 < 0
【答案】C
【解析】由题意 SKIPIF 1 < 0 ,∴ SKIPIF 1 < 0 .
故选:C.
2.若复数 SKIPIF 1 < 0 满足 SKIPIF 1 < 0 ,其中 SKIPIF 1 < 0 为虚数单位,则 SKIPIF 1 < 0 的实部为( )
A. SKIPIF 1 < 0 B. SKIPIF 1 < 0 C. SKIPIF 1 < 0 D. SKIPIF 1 < 0
【答案】B
【解析】设 SKIPIF 1 < 0 ,则 SKIPIF 1 < 0 ,
所以 SKIPIF 1 < 0 ,所以 SKIPIF 1 < 0 ,解得 SKIPIF 1 < 0 .
所以 SKIPIF 1 < 0 ,所以 SKIPIF 1 < 0 的实部为 SKIPIF 1 < 0 ,
故选:B.
3.已知命题 SKIPIF 1 < 0 SKIPIF 1 < 0 ;命题 SKIPIF 1 < 0 , SKIPIF 1 < 0 .则下列命题中是真命题的为( )
A. SKIPIF 1 < 0 B. SKIPIF 1 < 0 C. SKIPIF 1 < 0 D. SKIPIF 1 < 0
【答案】C
【解析】取 SKIPIF 1 < 0 ,可知 SKIPIF 1 < 0 ,故命题 SKIPIF 1 < 0 为真;
因为 SKIPIF 1 < 0 ,当且仅当 SKIPIF 1 < 0 时等号成立,故命题 SKIPIF 1 < 0 为真;
故 SKIPIF 1 < 0 为真,
故选:C.
4.本次模拟考试结束后,班级要排一张语文、数学、英语、物理、化学、生物六科试卷讲评顺序表,若化学排在生物前面,数学与物理不相邻且都不排在最后,则不同的排表方法共有( )
A.72种B.144种C.288种D.360种
【答案】B
【解析】第一步排语文,英语,化学,生物4种,且化学排在生物前面,有 SKIPIF 1 < 0 种排法;第二步将数学和物理插入前4科除最后位置外的4个空挡中的2个,有 SKIPIF 1 < 0 种排法,所以不同的排表方法共有 SKIPIF 1 < 0 种.
选 SKIPIF 1 < 0 .
5.Lgistic模型是常用数学模型之一,可应用于流行病学领域.有学者根据公布数据建立了某地区新冠肺炎累计确诊病例数 SKIPIF 1 < 0 ( SKIPIF 1 < 0 的单位:天)的Lgistic模型: SKIPIF 1 < 0 ,其中 SKIPIF 1 < 0 为最大确诊病例数.当 SKIPIF 1 < 0 时,标志着已初步遏制疫情,则 SKIPIF 1 < 0 约为( )(参考数据: SKIPIF 1 < 0 )
A.60B.62C.66D.63
【答案】D
【解析】 SKIPIF 1 < 0 SKIPIF 1 < 0 ,所以 SKIPIF 1 < 0 ,
所以 SKIPIF 1 < 0 ,解得 SKIPIF 1 < 0 .
故选:D.
6.已知正数 SKIPIF 1 < 0 是关于 SKIPIF 1 < 0 的方程 SKIPIF 1 < 0 的两根,则 SKIPIF 1 < 0 的最小值为( )
A.2B. SKIPIF 1 < 0 C.4D. SKIPIF 1 < 0
【答案】C
【解析】由题意,正数 SKIPIF 1 < 0 是关于 SKIPIF 1 < 0 的方程 SKIPIF 1 < 0 的两根,
可得 SKIPIF 1 < 0 ,
则 SKIPIF 1 < 0 ,当且仅当 SKIPIF 1 < 0 时,即 SKIPIF 1 < 0 时等号成立,
经检验知当 SKIPIF 1 < 0 时,方程 SKIPIF 1 < 0 有两个正实数解.
所以 SKIPIF 1 < 0 的最小值为 SKIPIF 1 < 0 .
故选:C.
7.已知双曲线C: SKIPIF 1 < 0 (a>0,b>0)的右焦点为F,点A,B分别为双曲线的左,右顶点,以AB为直径的圆与双曲线C的两条渐近线在第一,二象限分别交于P,Q两点,若OQ∥PF(O为坐标原点),则该双曲线的离心率为( )
A. SKIPIF 1 < 0 B.2C. SKIPIF 1 < 0 D. SKIPIF 1 < 0
【答案】D
【解析】如图所示, SKIPIF 1 < 0 ,
又 SKIPIF 1 < 0 双曲线的渐近线关于 SKIPIF 1 < 0 轴对称, SKIPIF 1 < 0 , SKIPIF 1 < 0 为等腰三角形,
作 SKIPIF 1 < 0 ,垂足为 SKIPIF 1 < 0 ,过 SKIPIF 1 < 0 作 SKIPIF 1 < 0 轴,交渐近线第一象限部分于 SKIPIF 1 < 0 ,
则 SKIPIF 1 < 0 , SKIPIF 1 < 0 ,
SKIPIF 1 < 0 .
由三角形相似的性质得 SKIPIF 1 < 0 ,即 SKIPIF 1 < 0 ,
整理得 SKIPIF 1 < 0 ,
故选:D.
8.定义在 SKIPIF 1 < 0 上的函数 SKIPIF 1 < 0 的导函数为 SKIPIF 1 < 0 ,若 SKIPIF 1 < 0 ,则不等式 SKIPIF 1 < 0 的解集是( )
A. SKIPIF 1 < 0 B. SKIPIF 1 < 0 C. SKIPIF 1 < 0 D. SKIPIF 1 < 0
【答案】D
【解析】由题意得: SKIPIF 1 < 0 ,即 SKIPIF 1 < 0 SKIPIF 1 < 0
故函数 SKIPIF 1 < 0 在 SKIPIF 1 < 0 上单调递减
SKIPIF 1 < 0 ,即 SKIPIF 1 < 0 SKIPIF 1 < 0
即 SKIPIF 1 < 0 SKIPIF 1 < 0 ,解得 SKIPIF 1 < 0
本题正确选项: SKIPIF 1 < 0
二、选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分.
9.为比较甲、乙两地某月14时的气温状况,随机选取该月中的5天,将这5天中14时的气温数据(单位:℃)制成如图所示的茎叶图.考虑以下结论:其中根据茎叶图能得到的统计结论为( )
A.甲地该月14时的平均气温低于乙地该月14时的平均气温;
B.甲地该月14时的平均气温高于乙地该月14时的平均气温;
C.甲地该月14时的平均气温的标准差小于乙地该月14时的气温的标准差;
D.甲地该月14时的平均气温的标准差大于乙地该月14时的气温的标准差.
【答案】AD
【解析】由茎叶图中的数据,我们可得甲、乙甲,乙两地某月14时的气温抽取的样本温度分别为:
甲:26,28,29,31,31
乙:28,29,30,31,32;
可得:甲地该月14时的平均气温: SKIPIF 1 < 0 (26+28+29+31+31)=29,
乙地该月14时的平均气温: SKIPIF 1 < 0 (28+29+30+31+32)=30,
故甲地该月14时的平均气温低于乙地该月14时的平均气温;
由方差公式可得:甲地该月14时温度的方差为:
SKIPIF 1 < 0
乙地该月14时温度的方差为:
SKIPIF 1 < 0 ,
所以甲地该月14时的气温的标准差大于乙地该月14时的气温标准差.
故选:AD
10.已知函数 SKIPIF 1 < 0 ,下列结论正确的是( )
A. SKIPIF 1 < 0 的最小正周期为 SKIPIF 1 < 0
B.函数 SKIPIF 1 < 0 的图象关于直线 SKIPIF 1 < 0 对称.
C.函数 SKIPIF 1 < 0 在 SKIPIF 1 < 0 上单调递增
D.方程 SKIPIF 1 < 0 在 SKIPIF 1 < 0 上有 SKIPIF 1 < 0 个不同的实根
【答案】ABD
【解析】由题意,函数 SKIPIF 1 < 0 ,
作出 SKIPIF 1 < 0 在 SKIPIF 1 < 0 上的图象,
将 SKIPIF 1 < 0 的图象向下平移 SKIPIF 1 < 0 个单位可得到 SKIPIF 1 < 0 的图象,
将所得图象在 SKIPIF 1 < 0 轴下方的部分沿 SKIPIF 1 < 0 轴翻折,
如图所示,由图可知 SKIPIF 1 < 0 的最小正周期为 SKIPIF 1 < 0 ,故 SKIPIF 1 < 0 正确;
曲线 SKIPIF 1 < 0 关于直线 SKIPIF 1 < 0 对称,故 SKIPIF 1 < 0 正确;
函数 SKIPIF 1 < 0 在 SKIPIF 1 < 0 上单调递减,则 SKIPIF 1 < 0 错误;
方程 SKIPIF 1 < 0 在 SKIPIF 1 < 0 上有 SKIPIF 1 < 0 个不同的实根,所以 SKIPIF 1 < 0 正确.
故选:ABD.
11.在数列 SKIPIF 1 < 0 中, SKIPIF 1 < 0 和 SKIPIF 1 < 0 是关于 SKIPIF 1 < 0 的一元二次方程 SKIPIF 1 < 0 的两个根,下列说法正确的是( )
A.实数 SKIPIF 1 < 0 的取值范围是 SKIPIF 1 < 0 或 SKIPIF 1 < 0
B.若数列 SKIPIF 1 < 0 为等差数列,则数列 SKIPIF 1 < 0 的前7项和为 SKIPIF 1 < 0
C.若数列 SKIPIF 1 < 0 为等比数列且 SKIPIF 1 < 0 ,则 SKIPIF 1 < 0
D.若数列 SKIPIF 1 < 0 为等比数列且 SKIPIF 1 < 0 ,则 SKIPIF 1 < 0 的最小值为4
【答案】AD
【解析】解:对A, SKIPIF 1 < 0 有两个根,
SKIPIF 1 < 0 ,
解得: SKIPIF 1 < 0 或 SKIPIF 1 < 0 ,故A正确;
对B,若数列 SKIPIF 1 < 0 为等差数列,
SKIPIF 1 < 0 和 SKIPIF 1 < 0 是关于 SKIPIF 1 < 0 的一元二次方程 SKIPIF 1 < 0 的两个根,
SKIPIF 1 < 0 ,
则 SKIPIF 1 < 0 ,故B错误;
对C,若数列 SKIPIF 1 < 0 为等比数列且 SKIPIF 1 < 0 ,由韦达定理得: SKIPIF 1 < 0 ,
可得: SKIPIF 1 < 0 , SKIPIF 1 < 0 ,
SKIPIF 1 < 0 ,
由等比数列的性质得: SKIPIF 1 < 0 ,
即 SKIPIF 1 < 0 ,故C错误;
对D,由C可知: SKIPIF 1 < 0 ,且 SKIPIF 1 < 0 , SKIPIF 1 < 0 ,
SKIPIF 1 < 0 ,当且仅当 SKIPIF 1 < 0 时,等号成立,故D正确.
故选AD.
12.如图,在正方体 SKIPIF 1 < 0 中,点 SKIPIF 1 < 0 在线段 SKIPIF 1 < 0 上运动时,下列命题正确的是( )
A.三棱锥 SKIPIF 1 < 0 的体积不变B.直线 SKIPIF 1 < 0 与平面 SKIPIF 1 < 0 所成角的大小不变
C.直线 SKIPIF 1 < 0 与直线 SKIPIF 1 < 0 所成角的大小不变D.二面角 SKIPIF 1 < 0 的大小不变
【答案】ACD
【解析】A: SKIPIF 1 < 0 平面 SKIPIF 1 < 0 , SKIPIF 1 < 0 上任意一点到平面 SKIPIF 1 < 0 的距离相等,所以体积不变,A选项正确;
B: SKIPIF 1 < 0 与平面 SKIPIF 1 < 0 相交,所以直线 SKIPIF 1 < 0 与平面 SKIPIF 1 < 0 所成角的大小在变,B选项错误;
C: SKIPIF 1 < 0 直线 SKIPIF 1 < 0 平面 SKIPIF 1 < 0 , SKIPIF 1 < 0 , SKIPIF 1 < 0 直线 SKIPIF 1 < 0 与直线 SKIPIF 1 < 0 所成角的大小不变;C选项正确;
D:二面角 SKIPIF 1 < 0 也就是二面角 SKIPIF 1 < 0 大小不变,D选项正确;
故选:ACD.
三、填空题:本题共4小题,每小题5分,共20分.
13.已知向量 SKIPIF 1 < 0 , SKIPIF 1 < 0 的夹角为 SKIPIF 1 < 0 , SKIPIF 1 < 0 , SKIPIF 1 < 0 ,若 SKIPIF 1 < 0 ,则 SKIPIF 1 < 0 ___________.
【答案】 SKIPIF 1 < 0
【解析】因为 SKIPIF 1 < 0 ,
所以 SKIPIF 1 < 0 SKIPIF 1 < 0 ,
所以 SKIPIF 1 < 0 ,
所以 SKIPIF 1 < 0 ,
所以 SKIPIF 1 < 0 ,
所以 SKIPIF 1 < 0 ,
所以 SKIPIF 1 < 0 .
故答案为: SKIPIF 1 < 0 .
14.如图,某湖有一半径为100 SKIPIF 1 < 0 的半圆形岸边,现决定在圆心O处设立一个水文监测中心(大小忽略不计),在其正东方向相距200 SKIPIF 1 < 0 的点A处安装一套监测设备.为了监测数据更加准确,在半圆弧上的点B以及湖中的点C处,再分别安装一套监测设备,且满足 SKIPIF 1 < 0 , SKIPIF 1 < 0 .定义:四边形 SKIPIF 1 < 0 及其内部区域为“直接监测覆盖区域”;设 SKIPIF 1 < 0 .则“直接监测覆盖区域”面积的最大值为___________.
【答案】 SKIPIF 1 < 0
【解析】在 SKIPIF 1 < 0 中, SKIPIF 1 < 0 , SKIPIF 1 < 0 , SKIPIF 1 < 0 ,
SKIPIF 1 < 0 ,即 SKIPIF 1 < 0 ,
SKIPIF 1 < 0 ,
SKIPIF 1 < 0
令 SKIPIF 1 < 0 ,则 SKIPIF 1 < 0
SKIPIF 1 < 0 直接监测覆盖区域”面积的最大值为 SKIPIF 1 < 0 .
故答案为: SKIPIF 1 < 0
15.已知等比数列 SKIPIF 1 < 0 的前 SKIPIF 1 < 0 项积为 SKIPIF 1 < 0 ,若 SKIPIF 1 < 0 ,则 SKIPIF 1 < 0 ___________.
【答案】512
【解析】因为 SKIPIF 1 < 0 ,由等比数列的性质,可得 SKIPIF 1 < 0 ,所以 SKIPIF 1 < 0 ,解得 SKIPIF 1 < 0 ,
又由 SKIPIF 1 < 0 .
故答案为: SKIPIF 1 < 0
16.已知双曲线M: SKIPIF 1 < 0 的渐近线是边长为1的菱形 SKIPIF 1 < 0 的边 SKIPIF 1 < 0 , SKIPIF 1 < 0 所在直线.若椭圆N: SKIPIF 1 < 0 ( SKIPIF 1 < 0 )经过A,C两点,且点B是椭圆N的一个焦点,则 SKIPIF 1 < 0 ______.
【答案】 SKIPIF 1 < 0
【解析】因为 SKIPIF 1 < 0 为双曲线 SKIPIF 1 < 0 的渐近线,所以 SKIPIF 1 < 0 ,则 SKIPIF 1 < 0
所以 SKIPIF 1 < 0 , SKIPIF 1 < 0 ,则 SKIPIF 1 < 0
因为 SKIPIF 1 < 0 ,所以椭圆 SKIPIF 1 < 0 的半焦距 SKIPIF 1 < 0
设椭圆 SKIPIF 1 < 0 的左焦点为 SKIPIF 1 < 0 ,则 SKIPIF 1 < 0 ,连接 SKIPIF 1 < 0
由椭圆的定义可得 SKIPIF 1 < 0
即 SKIPIF 1 < 0 ,解得 SKIPIF 1 < 0
故答案为: SKIPIF 1 < 0
四、解答题:本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.
17.如图,在 SKIPIF 1 < 0 中, SKIPIF 1 < 0 , SKIPIF 1 < 0 ,点 SKIPIF 1 < 0 在 SKIPIF 1 < 0 边上, SKIPIF 1 < 0 , SKIPIF 1 < 0 为锐角.
(1)若 SKIPIF 1 < 0 ,求 SKIPIF 1 < 0 的长度;
(2)若 SKIPIF 1 < 0 ,求 SKIPIF 1 < 0 的值.
【答案】(1) SKIPIF 1 < 0 ;(2) SKIPIF 1 < 0 .
【解析】(1)在 SKIPIF 1 < 0 中,由余弦定理得 SKIPIF 1 < 0 ,
所以 SKIPIF 1 < 0 ,解得 SKIPIF 1 < 0 或 SKIPIF 1 < 0 .
当 SKIPIF 1 < 0 时, SKIPIF 1 < 0 ,
则 SKIPIF 1 < 0 ,不合题意,舍去;
当 SKIPIF 1 < 0 时, SKIPIF 1 < 0 ,
则 SKIPIF 1 < 0 ,符合题意.
故 SKIPIF 1 < 0 .
在 SKIPIF 1 < 0 中, SKIPIF 1 < 0 ,
所以 SKIPIF 1 < 0 ,得 SKIPIF 1 < 0 ,
所以 SKIPIF 1 < 0 .
(2)记 SKIPIF 1 < 0 ,则 SKIPIF 1 < 0 .
在 SKIPIF 1 < 0 中, SKIPIF 1 < 0 ,
所以 SKIPIF 1 < 0 为锐角, SKIPIF 1 < 0 , SKIPIF 1 < 0 ,
所以 SKIPIF 1 < 0 , SKIPIF 1 < 0 ,
所以 SKIPIF 1 < 0 ,
同理 SKIPIF 1 < 0 .
易得 SKIPIF 1 < 0 ,
所以 SKIPIF 1 < 0 .
18.已知等比数列 SKIPIF 1 < 0 的公比为q.
(1)试问数列 SKIPIF 1 < 0 一定是等比数列吗?说明你的理由;
(2)在① SKIPIF 1 < 0 ,② SKIPIF 1 < 0 ,③ SKIPIF 1 < 0 这三个条件中任选两个,补充在下面的问题中并解答.
问题:若 ,求 SKIPIF 1 < 0 的通项公式及数列 SKIPIF 1 < 0 的前n项和 SKIPIF 1 < 0 .
注:如果选择多种情况解答,则按第一种情况计分.
【答案】(1)不一定, SKIPIF 1 < 0 时,不是等比数列;(2)答案见解析.
【解析】(1)数列 SKIPIF 1 < 0 不一定是等比数列,理由如下:
SKIPIF 1 < 0 时, SKIPIF 1 < 0 , SKIPIF 1 < 0 不是等比数列,
SKIPIF 1 < 0 时, SKIPIF 1 < 0 是等比数列,
故数列 SKIPIF 1 < 0 不一定是等比数列;
(2)选①②,
由 SKIPIF 1 < 0 , SKIPIF 1 < 0 得 SKIPIF 1 < 0 , SKIPIF 1 < 0 ,∵ SKIPIF 1 < 0 ,∴ SKIPIF 1 < 0 ,
∴ SKIPIF 1 < 0 ,
SKIPIF 1 < 0 ,
SKIPIF 1 < 0 为偶数时, SKIPIF 1 < 0 ,
SKIPIF 1 < 0 为奇数时, SKIPIF 1 < 0 ,
选②③,
由 SKIPIF 1 < 0 , SKIPIF 1 < 0 得 SKIPIF 1 < 0 , SKIPIF 1 < 0 ,又 SKIPIF 1 < 0 , SKIPIF 1 < 0 ,
∴ SKIPIF 1 < 0 , SKIPIF 1 < 0 ,∴ SKIPIF 1 < 0 ,
SKIPIF 1 < 0 ,
当 SKIPIF 1 < 0 为偶数时, SKIPIF 1 < 0 ,
当 SKIPIF 1 < 0 为奇数时, SKIPIF 1 < 0 ;
选①③,
由 SKIPIF 1 < 0 ,得 SKIPIF 1 < 0 ,又 SKIPIF 1 < 0 ,∴ SKIPIF 1 < 0 ,∴ SKIPIF 1 < 0 ,
SKIPIF 1 < 0 ,
SKIPIF 1 < 0 为偶数时, SKIPIF 1 < 0 ,
SKIPIF 1 < 0 为奇数时, SKIPIF 1 < 0 ,
19.甲、乙两人想参加某项竞赛,根据以往20次的测试分别获得甲、乙测试成绩的频率分布直方图.
已知甲测试成绩的中位数为75.
(1)求 SKIPIF 1 < 0 , SKIPIF 1 < 0 的值,并分别求出甲、乙两人测试成绩的平均数(假设同一组中的每个数据可用该组区间中点值代替).
(2)某学校参加该项竞赛仅有一个名额,结合平时的训练成绩甲、乙两名学生进入最后选拔,学校为此设计了如下选拔方案:答题过程中,若答对则继续答题,若答错则换对方答题例如,若甲首先答题,则他答第1题,若答对继续答第2题如果第2题也答对,继续答第3题,直到他答错则换成乙开始答题,……,直到乙答错再换成甲答题依次类推两人共计答完21道题时答题结束,答对题目数量多者胜出.已知甲、乙两人答对其中每道题的概率都是 SKIPIF 1 < 0 ,假设由以往20次的测试成绩平均分高的同学在选拔比赛中最先开始作答,且记第 SKIPIF 1 < 0 道题也由该同学(最先答题的同学)作答的概率为 SKIPIF 1 < 0 ,其中 SKIPIF 1 < 0
①求 SKIPIF 1 < 0 , SKIPIF 1 < 0 ;
②求证 SKIPIF 1 < 0 为等比数列,并求 SKIPIF 1 < 0 的表达式.
【答案】(1) SKIPIF 1 < 0 . SKIPIF 1 < 0 ,甲74.5,乙73.5;(2)① SKIPIF 1 < 0 , SKIPIF 1 < 0 ;②证明见解析, SKIPIF 1 < 0 .
【解析】解:(1)∵甲测试成绩的中位数为75,
∴ SKIPIF 1 < 0 ,解得 SKIPIF 1 < 0 .
∴ SKIPIF 1 < 0 ,解得 SKIPIF 1 < 0 .
同学甲的平均分为 SKIPIF 1 < 0 .
同学乙的平均分为 SKIPIF 1 < 0 .
(2)由(1)可知甲的平均分大于乙的平均分,则甲最先答题.
①依题意知 SKIPIF 1 < 0 , SKIPIF 1 < 0 , SKIPIF 1 < 0 ,
②依题意知第 SKIPIF 1 < 0 次由甲答题,则若第 SKIPIF 1 < 0 次甲答题且答对,则第 SKIPIF 1 < 0 次甲答题;若第 SKIPIF 1 < 0 次乙答题且答错,则第 SKIPIF 1 < 0 次甲答题.
所以 SKIPIF 1 < 0 .
∴ SKIPIF 1 < 0 , SKIPIF 1 < 0 .
又 SKIPIF 1 < 0 ,∴ SKIPIF 1 < 0 是以 SKIPIF 1 < 0 为首项, SKIPIF 1 < 0 为比的等比数列,
∴ SKIPIF 1 < 0 ,∴ SKIPIF 1 < 0 .
20.如图,在三棱柱 SKIPIF 1 < 0 中,侧面 SKIPIF 1 < 0 为正方形,点 SKIPIF 1 < 0 、 SKIPIF 1 < 0 分别是 SKIPIF 1 < 0 、 SKIPIF 1 < 0 的中点, SKIPIF 1 < 0 平面 SKIPIF 1 < 0 .
(Ⅰ)求证: SKIPIF 1 < 0 平面 SKIPIF 1 < 0 ;
(Ⅱ)若 SKIPIF 1 < 0 是边长为 SKIPIF 1 < 0 的菱形,求直线 SKIPIF 1 < 0 与平面 SKIPIF 1 < 0 所成角的正弦值.
【答案】(Ⅰ)证明见解析;(Ⅱ) SKIPIF 1 < 0 .
【解析】解:(Ⅰ)证明:设 SKIPIF 1 < 0 的中点为Q,连接 SKIPIF 1 < 0 , SKIPIF 1 < 0 ,
因为 SKIPIF 1 < 0 、 SKIPIF 1 < 0 分别为 SKIPIF 1 < 0 , SKIPIF 1 < 0 的中点,所以 SKIPIF 1 < 0 ,且 SKIPIF 1 < 0 ,又 SKIPIF 1 < 0 ,且 SKIPIF 1 < 0 ,所以 SKIPIF 1 < 0 ,且 SKIPIF 1 < 0 ,所以四边形 SKIPIF 1 < 0 为平行四边形.
所以 SKIPIF 1 < 0 ,又因为 SKIPIF 1 < 0 平面 SKIPIF 1 < 0 , SKIPIF 1 < 0 平面 SKIPIF 1 < 0 ,
所以 SKIPIF 1 < 0 平面 SKIPIF 1 < 0 .
(Ⅱ) SKIPIF 1 < 0 平面 SKIPIF 1 < 0 , SKIPIF 1 < 0 , SKIPIF 1 < 0 平面 SKIPIF 1 < 0 , SKIPIF 1 < 0 , SKIPIF 1 < 0 ,
又 SKIPIF 1 < 0 , SKIPIF 1 < 0 , SKIPIF 1 < 0 ,所以 SKIPIF 1 < 0 平面 SKIPIF 1 < 0 .
于是以 SKIPIF 1 < 0 , SKIPIF 1 < 0 , SKIPIF 1 < 0 分别为 SKIPIF 1 < 0 , SKIPIF 1 < 0 , SKIPIF 1 < 0 轴建立平面直角坐标系 SKIPIF 1 < 0 ,
如图,因为 SKIPIF 1 < 0 是边长为 SKIPIF 1 < 0 的菱形,且 SKIPIF 1 < 0 ,得 SKIPIF 1 < 0 ,
所以各点坐标: SKIPIF 1 < 0 , SKIPIF 1 < 0 , SKIPIF 1 < 0 , SKIPIF 1 < 0
SKIPIF 1 < 0 , SKIPIF 1 < 0 , SKIPIF 1 < 0 , SKIPIF 1 < 0
则 SKIPIF 1 < 0 , SKIPIF 1 < 0 , SKIPIF 1 < 0
设平面 SKIPIF 1 < 0 的法向量为 SKIPIF 1 < 0 ,则 SKIPIF 1 < 0 ,即 SKIPIF 1 < 0
则 SKIPIF 1 < 0 ,设直线 SKIPIF 1 < 0 与 SKIPIF 1 < 0 所成角为 SKIPIF 1 < 0 .
则 SKIPIF 1 < 0 .
21.设函数 SKIPIF 1 < 0 ,
(I)求函数 SKIPIF 1 < 0 的单调区间;
(Ⅱ)设对于任意 SKIPIF 1 < 0 ,且 SKIPIF 1 < 0 ,都有 SKIPIF 1 < 0 恒成立,求实数 SKIPIF 1 < 0 的取值范围.
【答案】(I) SKIPIF 1 < 0 的单调递减区间是 SKIPIF 1 < 0 ,单调递增区间是 SKIPIF 1 < 0 ;(Ⅱ) SKIPIF 1 < 0 .
【解析】(I)易知 SKIPIF 1 < 0 的定义域为R,
SKIPIF 1 < 0 ,当 SKIPIF 1 < 0 时, SKIPIF 1 < 0 在 SKIPIF 1 < 0 上单调递增,
当 SKIPIF 1 < 0 时, SKIPIF 1 < 0 在 SKIPIF 1 < 0 上单调递减.
SKIPIF 1 < 0 的单调递减区间是 SKIPIF 1 < 0 ,单调递增区间是 SKIPIF 1 < 0 .
(Ⅱ)当 SKIPIF 1 < 0 , SKIPIF 1 < 0 时, SKIPIF 1 < 0 恒成立,即 SKIPIF 1 < 0 恒成立,设 SKIPIF 1 < 0 ,由题意可知, SKIPIF 1 < 0 在 SKIPIF 1 < 0 上单调递减,
即 SKIPIF 1 < 0 在 SKIPIF 1 < 0 上恒成立;
SKIPIF 1 < 0 ,
设 SKIPIF 1 < 0 ,则 SKIPIF 1 < 0 在 SKIPIF 1 < 0 上单调递减,
SKIPIF 1 < 0 ,即 SKIPIF 1 < 0
22.已知椭圆 SKIPIF 1 < 0 经过点 SKIPIF 1 < 0 ,且右焦点 SKIPIF 1 < 0 .
(1)求椭圆 SKIPIF 1 < 0 的标准方程;
(2)过 SKIPIF 1 < 0 且斜率存在的直线 SKIPIF 1 < 0 交椭圆 SKIPIF 1 < 0 于 SKIPIF 1 < 0 , SKIPIF 1 < 0 两点,记 SKIPIF 1 < 0 ,若 SKIPIF 1 < 0 的最大值和最小值分别为 SKIPIF 1 < 0 , SKIPIF 1 < 0 ,求 SKIPIF 1 < 0 的值.
【答案】(1) SKIPIF 1 < 0 ;(2) SKIPIF 1 < 0 .
【解析】(1)由椭圆 SKIPIF 1 < 0 的右焦点为 SKIPIF 1 < 0 ,知 SKIPIF 1 < 0 ,即 SKIPIF 1 < 0 ,则 SKIPIF 1 < 0 , SKIPIF 1 < 0 .
又椭圆过点 SKIPIF 1 < 0 ,∴ SKIPIF 1 < 0 ,又 SKIPIF 1 < 0 ,∴ SKIPIF 1 < 0 .
∴椭圆 SKIPIF 1 < 0 的标准方程为 SKIPIF 1 < 0 .
(2)设直线 SKIPIF 1 < 0 的方程为 SKIPIF 1 < 0 , SKIPIF 1 < 0 , SKIPIF 1 < 0
由 SKIPIF 1 < 0 得 SKIPIF 1 < 0 ,即 SKIPIF 1 < 0
∵点 SKIPIF 1 < 0 在椭圆内部,∴ SKIPIF 1 < 0
∴由韦达定理可得: SKIPIF 1 < 0 (*)
则 SKIPIF 1 < 0
SKIPIF 1 < 0
SKIPIF 1 < 0
SKIPIF 1 < 0
将(*)代入上式得: SKIPIF 1 < 0 ,
即 SKIPIF 1 < 0 , SKIPIF 1 < 0 ,则 SKIPIF 1 < 0
∴ SKIPIF 1 < 0 ,即 SKIPIF 1 < 0
由题意知 SKIPIF 1 < 0 , SKIPIF 1 < 0 是 SKIPIF 1 < 0 的两根
∴ SKIPIF 1 < 0 .
新高考数学模拟测试卷12(原卷版+解析版): 这是一份新高考数学模拟测试卷12(原卷版+解析版),共28页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
新高考数学模拟测试卷11(原卷版+解析版): 这是一份新高考数学模拟测试卷11(原卷版+解析版),共28页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
新高考数学模拟测试卷08(原卷版+解析版): 这是一份新高考数学模拟测试卷08(原卷版+解析版),共25页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。












