高考数学三轮冲刺卷：平面向量数量积的坐标运算（含答案）

这是一份高考数学三轮冲刺卷：平面向量数量积的坐标运算（含答案），共13页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

一、选择题（共20小题；）
1. 已知 ，，则 等于
A. B. C. D.

2. 已知 ，，，则
A. B. C. D.

3. 已知 ，，，则
A. B. C. D.

4. 已知 ，，若 ，则 的值为
A. B. C. D.

5. 已知向量 ，，则
A. B. C. D.

6. 在四边形 中，，，则该四边形的面积为
A. B. C. D.

7. 向量 ，，则 等于
A. B. C. D.

8. 已知四边形 是菱形，若 ，，则 的值是
A. B. C. D.

9. 已知向量 ，，则
A. B. C. D.

10. 在矩形 中，，， 与 相交于点 ，过点 作 ，垂足为 ，则
A. B. C. D.

11. 已知 ，， 是平面向量， 是单位向量．若非零向量 与 的夹角为 ，向量 满足 ，则 的最小值是
A. B. C. D.

12. 已知平面向量 ，， 与 垂直，则 等于
A. B. C. D.

13. 在平行四边形 中，，，，点 在边 上，则 的取值范围是
A. B. C. D.

14. 已知 ， 且 ，，则点 的坐标是
A. B. C. D.

15. 已知 ， 是半径为 的 上的两个点，， 所在平面上有一点 满足 ，则 的最大值为
A. B. C. D.

16. 如图，在平行四边形 中，，，，若 ， 分别是边 ， 上的点，且满足 ，其中 ，则 的取值范围是
A. B. C. D.

17. 若动点 ， 分别在直线 和 上移动，则 的中点 到原点的距离的最小值为
A. B. C. D.

18. 已知 ，则
A. B. C. D.

19. 抛物线 ： 的焦点为 ， 为准线上一点， 为 轴上一点， 为直角，若线段 的中点 在抛物线 上，则 的面积为
A. B. C. D.

20. 已知向量 ，向量 ，则 的最大值为
A. B. C. D.

二、填空题（共5小题；）
21. 已知向量 ，，，若 ，则 的值为 ．

22. 已知向量 ，，则 在 的方向上的投影为 ．

23. 设平面向量 ，，若 ，则 ．

24. 已知在矩形 中，，，， 分别为 ， 的中点，则 ．

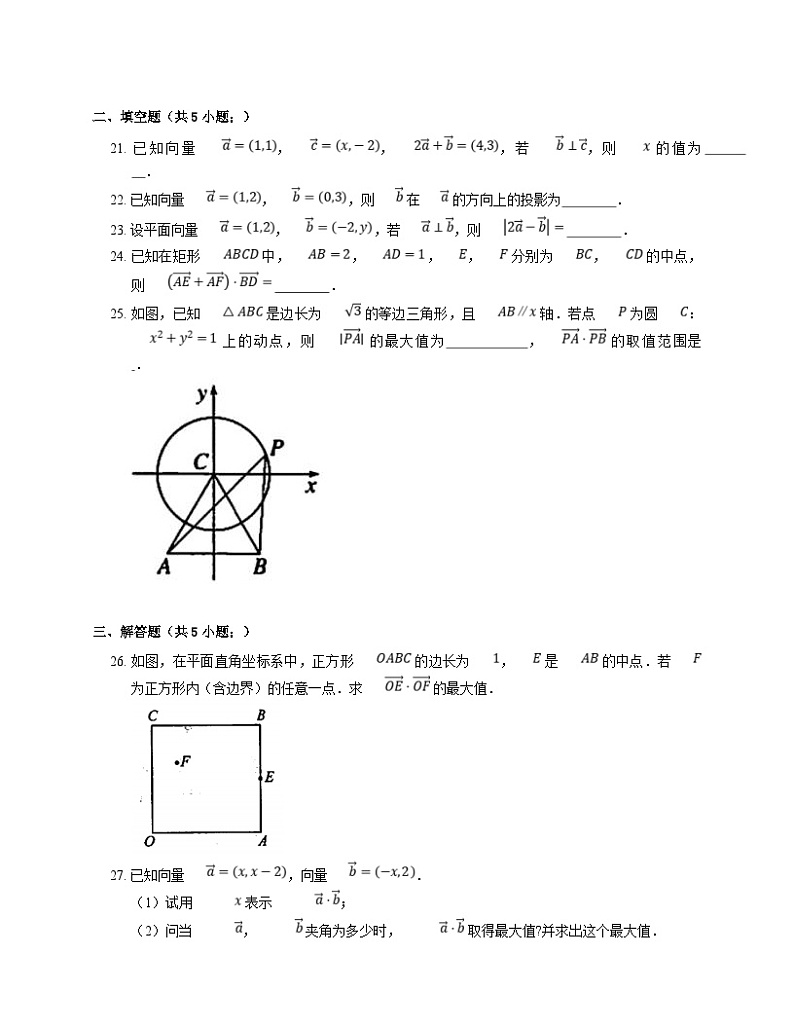
25. 如图，已知 是边长为 的等边三角形，且 轴．若点 为圆 ： 上的动点，则 的最大值为 ， 的取值范围是 ．

三、解答题（共5小题；）
26. 如图，在平面直角坐标系中，正方形 的边长为 ， 是 的中点．若 为正方形内（含边界）的任意一点．求 的最大值．

27. 已知向量 ，向量 ．
（1）试用 表示 ；
（2）问当 ， 夹角为多少时， 取得最大值?并求出这个最大值．

28. 如图，已知菱形 中，点 为线段 上一点，且 ．
（1）若 ，，求 ， 的值；
（2）若 ，且 ，求实数 的取值范围．

29. 已知四边形 为平行四边形，点 的坐标为 ，点 在第二象限，，且 与 的夹角为 ，．
（1）求点 的坐标；
（2）当 为何值时， 与 垂直．

30. 设双曲线 的左顶点为 ，且以点 为圆心的圆 与双曲线 分别相交于点 ，，如图所示．
（1）求双曲线 的方程；
（2）求 的最小值，并求出此时圆 的方程；
（3）设点 为双曲线 上异于点 ， 的任意一点，且直线 ， 分别与 轴相交于点 ，．求证： 为定值（其中 为坐标原点）．
答案
1. B【解析】，，
所以 ．
2. C
3. C
4. D【解析】因为 ，，
所以 ，，
又 ，，
所以 ，则 ．
5. A
6. C【解析】因为在四边形 中，，，，
所以四边形 的对角线互相垂直，
又 ，，
该四边形的面积：．
7. C【解析】因为 ，，
所以 ，
则 ．
8. D
9. A【解析】由题意，得 ，
所以 ，故选A．
10. D
【解析】建立平面直角坐标系，如图所示；
矩形 中，，，则 ，，，；
直线 的方程为 ；
由 ，则直线 的方程为 ，即 ；
由 解得 ，
所以 ，，
所以 ．
11. A【解析】设 为坐标原点，，，，
由 得 ，即 ，
所以点 的轨迹是以 为圆心， 为半径的圆．
因为 与 的夹角为 ，
所以不妨令点 在射线 上，如图，
数形结合可知 ．
12. C【解析】，
因为 与 垂直，
所以 ，
即 ，
解得 ．
13. A【解析】因为 ，，，
所以 ，
所以 ，
所以 ，
以 为原点，以 所在的直线为 轴，以 的垂线为 轴，建立如图所示的坐标系，
所以 ，，，
设 ，则 ，
所以 ，，
所以 ，
设 ，
所以 在 上单调递减，在 上单调递增，
所以 ，，
所以 的取值范围是 ．
14. D【解析】设 ，则 ，，，
因为 ，
所以
因为 ，
所以
由 可得
所以 ．
15. A
【解析】根据题意，，
因为 ，
所以 ，，
即 是等边三角形，建立图示直角坐标系，
则 ，，，，
，，
，
点 满足 ，
所以 ，
即点 在以 为圆心，以 为半径的圆上，
点 到圆心 的距离为 ，
点 到圆上一点的最大距离为 ，即 的最大值为 ．
16. B【解析】建立如图所示的以 为原点，， 所在直线为 ， 轴的直角坐标系．
则 ，，．
因为满足 ，，


则

因为 ，二次函数的对称轴为 ，则 为增区间，
故当 时，．
17. A【解析】依题意知动线段 的中点 的轨迹为与直线 和 等距的直线，
则 到原点的距离的最小值为原点到该直线的距离，
设点 的轨迹方程为 ，根据平行线间的距离公式得 ，
即点 的轨迹方程为 ，
根据点到直线的距离公式，得 到原点的距离的最小值为 ．
18. C【解析】．
故选C．
19. C【解析】如图所示，不妨设点 在第二象限，连接 ，易知 ，
因为 为直角，点 为线段 的中点，
所以 ，又 在抛物线 上，
所以 ，，
所以 ，，
所以 ，，
所以 的面积为 ．
20. D
21.
【解析】因为向量 ，，，
所以 ，
若 ，则 ，
则 ．
22.
【解析】．
23.
【解析】因为 ，，，
所以 ，
所以 ，
所以 ，
所以 ．
24.
【解析】如图，以 为坐标原点 ，以 所在直线为 轴，以 所在直线为 轴建立平面直角坐标系，
则 ，，，
所以 ．
因为 ， 分别为 ， 的中点，
所以 ，，
因为 ，，
所以 ．
25. ，
26. 设 为原点．
，，．
设 （其中 ，），
所以 ．
27. （1） ．
（2） ，
知 的最大值为 ，
此时 ，，
设夹角为 ，
则 ．
28. （1）
．
所以

所以
解得
（2） 以 为坐标原点，以 为 轴建立平面直角坐标系，
因为 ，
所以 是等边三角形，
设 ，则 ，，，．
所以 ，，，．
所以 ，，
因为 ，
所以 ．
解得 ，
又 ，
所以 ．
29. （1） 设 ，，则 ．
因为 与 的夹角为 ，，
所以 ，
即
又 ，即
联立①②解得 或
又点 在第二象限，所以 ．
又 ，所以 ，
解得 ，．所以 ．
（2） 由（）可知 ，
所以 ，．
因为 与 垂直，
所以 ，
解得 ．
30. （1） 由条件知：双曲线 的左焦点为 ，于是 ．
故双曲线 的方程为 ．
（2） 易知点 ， 关于 轴对称，设 ，，
则由点 在双曲线 上，得 ，
由于 ，，所以

因 ，故当 时，，
此时 ，即 ，
从而 ．
所以当 取最小值时，圆 的方程为 ．
（3） 设 ，则 ，
直线 的方程为 ，
令 ，得 ，
同理，可得 ．
因点 ， 在双曲线 上，故 ，，
于是

因此 为定值．