



【单元知识点归纳】(人教版)2023-2024学年八年级数学上册 第十一章 三角形(知识归纳+八大题型突破)
展开第十一章 三角形(知识归纳+八大题型突破)
1.理解三角形的定义,三边关系.
2.会作三角形的高线、中线、角平分线.
3.会证明三角形内角和的定理与外角和定理,并会求解多边形内角和与外角和.
一、三角形的定义
由不在同一条直线上的三条线段首尾顺次相接所组成的图形叫做三角形.
要点诠释:
(1)三角形的基本元素:
①三角形的边:即组成三角形的线段;
②三角形的角:即相邻两边所组成的角叫做三角形的内角,简称三角形的角;
③三角形的顶点:即相邻两边的公共端点.
(2)三角形的定义中的三个要求:“不在同一条直线上”、“三条线段”、“首尾顺次相接”.
(3)三角形的表示:三角形用符号“△”表示,顶点为A、B、C的三角形记作“△ABC”,读作“三角形ABC”,注意单独的△没有意义;△ABC的三边可以用大写字母AB、BC、AC来表示,也可以用小写字母a、b、c来表示,边BC用a表示,边AC、AB分别用b、c表示.
二、三角形的三边关系
定理:三角形任意两边之和大于第三边.
推论:三角形任意两边的之差小于第三边.
要点诠释:
(1)理论依据:两点之间线段最短.
(2)三边关系的应用:判断三条线段能否组成三角形,若两条较短的线段长之和大于最长线段的长,则这三条线段可以组成三角形;反之,则不能组成三角形.当已知三角形两边长,可求第三边长的取值范围.
(3)证明线段之间的不等关系.
三、三角形的分类
1.按角分类:
要点诠释:
①锐角三角形:三个内角都是锐角的三角形;
②钝角三角形:有一个内角为钝角的三角形.
2.按边分类:
要点诠释:
①不等边三角形:三边都不相等的三角形;
②等腰三角形:有两条边相等的三角形叫做等腰三角形,相等的两边都叫做腰,另外一边叫做底边,两腰的夹角叫顶角,腰与底边夹角叫做底角;
③等边三角形:三边都相等的三角形.
四、三角形的三条重要线段
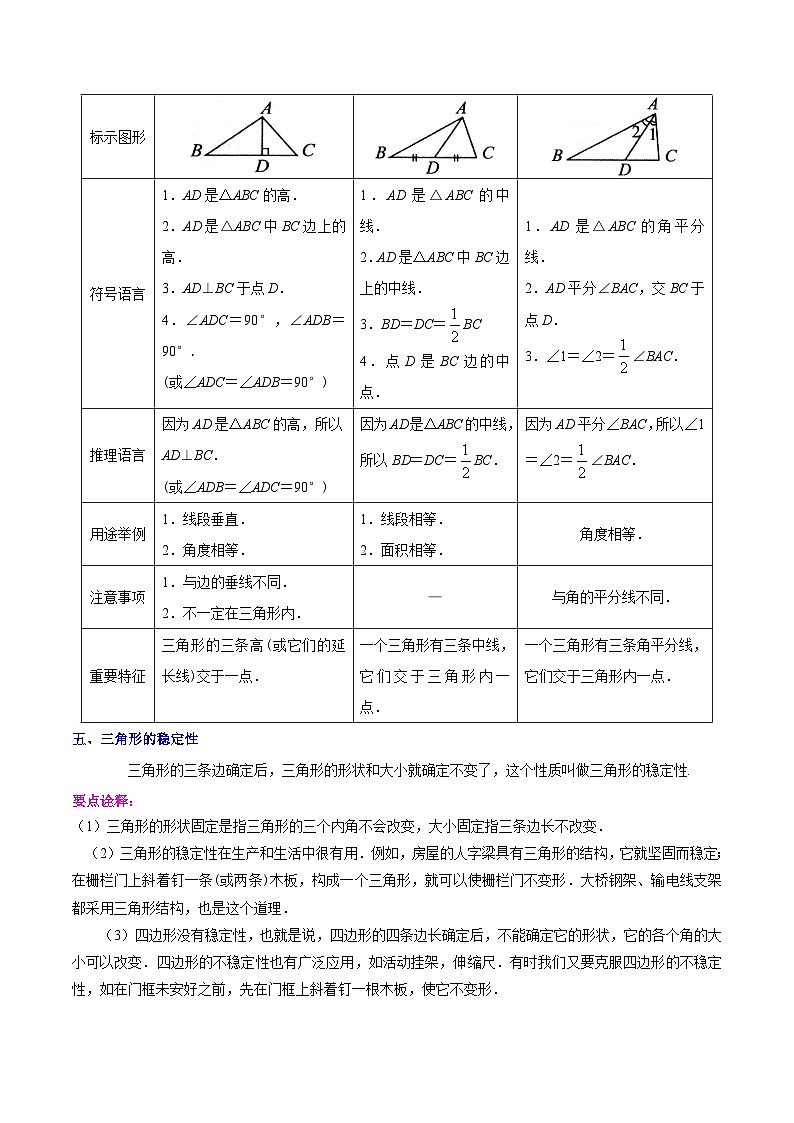
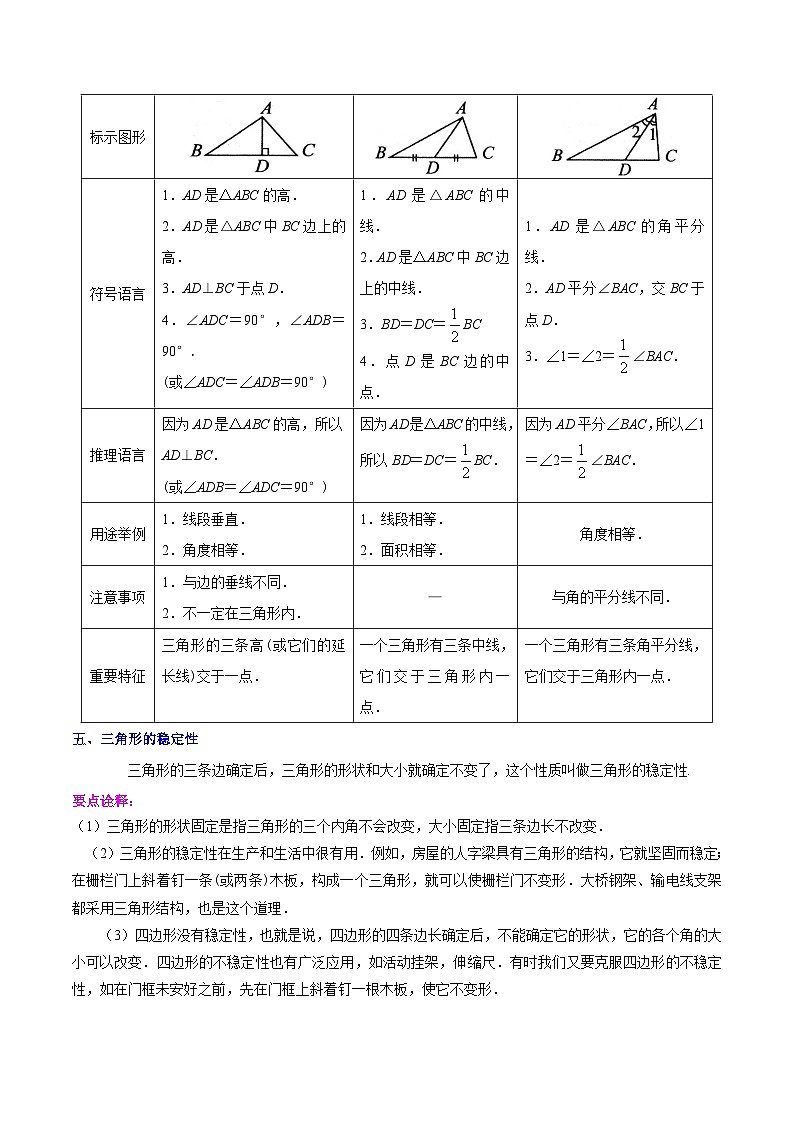
三角形的高、中线和角平分线是三角形中三条重要的线段,它们提供了重要的线段或角的关系,为我们以后深入研究三角形的一些特征起着很大的帮助作用,因此,我们需要从不同的角度弄清这三条线段,列表如下:
线段名称 | 三角形的高 | 三角形的中线 | 三角形的角平分线 |
文字语言 | 从三角形的一个顶点向它的对边所在的直线作垂线,顶点和垂足之间的线段. | 三角形中,连接一个顶点和它对边中点的线段. | 三角形一个内角的平分线与它的对边相交,这个角的顶点与交点之间的线段. |
图形语言 | |||
作图语言 | 过点A作AD⊥BC于点D. | 取BC边的中点D,连接AD. | 作∠BAC的平分线AD,交BC于点D. |
标示图形 | |||
符号语言 | 1.AD是△ABC的高. 2.AD是△ABC中BC边上的高. 3.AD⊥BC于点D. 4.∠ADC=90°,∠ADB=90°. (或∠ADC=∠ADB=90°) | 1.AD是△ABC的中线. 2.AD是△ABC中BC边上的中线. 3.BD=DC=BC 4.点D是BC边的中点. | 1.AD是△ABC的角平分线. 2.AD平分∠BAC,交BC于点D. 3.∠1=∠2=∠BAC. |
推理语言 | 因为AD是△ABC的高,所以AD⊥BC. (或∠ADB=∠ADC=90°) | 因为AD是△ABC的中线,所以BD=DC=BC. | 因为AD平分∠BAC,所以∠1=∠2=∠BAC. |
用途举例 | 1.线段垂直. 2.角度相等. | 1.线段相等. 2.面积相等. | 角度相等. |
注意事项 | 1.与边的垂线不同. 2.不一定在三角形内. | — | 与角的平分线不同. |
重要特征 | 三角形的三条高(或它们的延长线)交于一点. | 一个三角形有三条中线,它们交于三角形内一点. | 一个三角形有三条角平分线,它们交于三角形内一点. |
五、三角形的稳定性
三角形的三条边确定后,三角形的形状和大小就确定不变了,这个性质叫做三角形的稳定性.
要点诠释:
(1)三角形的形状固定是指三角形的三个内角不会改变,大小固定指三条边长不改变.
(2)三角形的稳定性在生产和生活中很有用.例如,房屋的人字梁具有三角形的结构,它就坚固而稳定;在栅栏门上斜着钉一条(或两条)木板,构成一个三角形,就可以使栅栏门不变形.大桥钢架、输电线支架都采用三角形结构,也是这个道理.
(3)四边形没有稳定性,也就是说,四边形的四条边长确定后,不能确定它的形状,它的各个角的大小可以改变.四边形的不稳定性也有广泛应用,如活动挂架,伸缩尺.有时我们又要克服四边形的不稳定性,如在门框未安好之前,先在门框上斜着钉一根木板,使它不变形.
六、三角形的内角和
三角形内角和定理:三角形的内角和为180°.
要点诠释:应用三角形内角和定理可以解决以下三类问题:
①在三角形中已知任意两个角的度数可以求出第三个角的度数;
②已知三角形三个内角的关系,可以求出其内角的度数;
③求一个三角形中各角之间的关系.
七、三角形的外角
1.定义:三角形的一边与另一边的延长线组成的角叫做三角形的外角.如图,∠ACD是△ABC的一个外角.
要点诠释:
(1)外角的特征:①顶点在三角形的一个顶点上; ②一条边是三角形的一边;③另一条边是三角形某条边的延长线.
(2)三角形每个顶点处有两个外角,它们是对顶角.所以三角形共有六个外角,通常每个顶点处取一个外角,因此,我们常说三角形有三个外角.
2.性质:
(1)三角形的一个外角等于与它不相邻的两个内角的和.
(2)三角形的一个外角大于任意一个与它不相邻的内角.
要点诠释:三角形内角和定理和三角形外角的性质是求角度及与角有关的推理论证明经常使用的理论依据.另外,在证角的不等关系时也常想到外角的性质.
3.三角形的外角和:
三角形的外角和等于360°.
要点诠释:因为三角形的每个外角与它相邻的内角是邻补角,由三角形的内角和是180°,可推出三角形的三个外角和是360°.
八、多边形的概念
1.定义:在平面内不在同一直线上的一些线段首尾顺次相接所组成的封闭图形叫做多边形.其中,各个角相等、各条边相等的多边形叫做正多边形.
2.相关概念:
边:组成多边形的各条线段叫做多边形的边.
顶点:每相邻两条边的公共端点叫做多边形的顶点.
内角:多边形相邻两边组成的角叫多边形的内角,一个n边形有n个内角.
外角:多边形的边与它的邻边的延长线组成的角叫做多边形的外角.
对角线:连接多边形不相邻的两个顶点的线段,叫做多边形的对角线.
3. 多边形的分类:画出多边形的任何一边所在的直线,如果整个多边形都在这条直线的同一侧,那么这个多边形就是凸多边形,如果整个多边形不在直线的同一侧,这个多边形叫凹多边形.如图:
要点诠释:
(1)正多边形必须同时满足“各边相等”,“各角相等”两个条件,二者缺一不可;
(2)过n边形的一个顶点可以引(n-3)条对角线,n边形对角线的条数为;
(3)过n边形的一个顶点的对角线可以把n边形分成(n-2)个三角形.
九、多边形内角和
n边形的内角和为(n-2)·180°(n≥3).
要点诠释:
(1)内角和公式的应用:①已知多边形的边数,求其内角和;②已知多边形内角和求其边数;(2)正多边形的每个内角都相等,都等于;
十、多边形的外角和
多边形的外角和为360°.
要点诠释:
(1)在一个多边形的每个顶点处各取一个外角,这些外角的和叫做多边形的外角和.n边形的外角和恒等于360°,它与边数的多少无关;
(2)正n边形的每个内角都相等,所以它的每个外角都相等,都等于;
(3)多边形的外角和为360°的作用是:①已知各相等外角度数求多边形边数;②已知多边形边数求各相等外角的度数.
题型一 三角形的稳定性
例题:(2023·山西运城·统考二模)学校、工厂、企业等单位的大门都是收缩性大门,这种门的门体可以伸缩自由移动,以此来控制门的大小.这种方法应用的数学知识是( )
A.三角形的稳定形 B.四边形的不稳定性
C.勾股定理 D.黄金分割
巩固训练
1.(2023秋·云南楚雄·八年级统考期末)西双版纳大桥是云南省境内一座桥梁,位于西双版纳州府景洪市,跨越澜沧江,是西双版纳十大标志性建筑之一,如图,西双版纳大桥中的斜拉索、索塔和桥面构成了一个三角形,这样使其更稳固,其中运用的数学原理是________.
2.(2023春·陕西西安·七年级陕西师大附中校考阶段练习)近日,中亚峰会于5月18日至19日在西安举行,暮色中的大唐芙蓉园流光溢彩,美轮美奂.工人师傅在楼阁上固定木制门框用来张贴欢迎条幅,为了防止变形常常像图中所示,钉上两条斜拉的木条,这样做的原理是___.
3.(2023春·九年级单元测试)如图,学校门口设置的移动拒马都用钢管焊接成三角形,这样做的数学原理是利用了三角形的_____(选填“稳定性”或“不稳定性”).
题型二 判断三边是否能构成三角形
例题:(2023春·黑龙江哈尔滨·七年级哈尔滨市第四十九中学校校考期中)下列每组数分别是三根小木棒的长度,用它们能摆成三角形的是( )
A.9,6,13 B.6,8,16 C.18,9,8 D.3,5,9
巩固训练
1.(2023春·湖南长沙·七年级长沙市长郡梅溪湖中学校考阶段练习)下列各组线段中,能构成三角形的是( )
A.2,5,8 B.3,3,6 C.3,4,5 D.4,5,9
2.(2023·浙江·八年级假期作业)如果三条线段长度的比是:①,②,③,④,⑤,⑥.那么其中可构成三角形的个数为( )
A.个 B.个 C.个 D.个
3.(2023春·安徽合肥·七年级统考阶段练习)长为9,6,5,3的四根木条,选其中三根组成三角形,共有( )种选法.
A.4 B.3 C.2 D.1
题型三 已知三角形的两边长,求第三边的取值范围
例题:(2023春·黑龙江绥化·七年级校联考期中)若一个三角形的两边长是4和9,且周长是偶数,则第三边长为_______.
巩固训练
1.(2023春·陕西西安·七年级西安市第二十六中学校考阶段练习)三角形的两边长分别是2、7,若第三边长为奇数,则此三角形第三边的长是______.
2.(2023·江苏连云港·统考中考真题)一个三角形的两边长分别是3和5,则第三边长可以是__________.(只填一个即可)
3.(2023·河北·统考模拟预测)已知一个三角形的第一条边长为,第二条边长为
(1)求第三条边长的取值范围;(用含,的式子表示)
(2)若,满足,第三条边长为整数,求这个三角形周长的最大值
题型四 与平行线有关的三角形内角和问题
例题:(2023·浙江·八年级假期作业)如图,在中,,过点作.若,则的度数为( )
A. B. C. D.
巩固训练
1.(2023春·陕西西安·七年级西安市第二十六中学校考阶段练习)如图,在中,,,,则的度数为( )
A. B. C. D.
2.(2023·湖南岳阳·统考三模)将一副直角三角板如图放置,已知,,,则为( )
A.45° B.60° C.90° D.105°
3.(2023春·陕西咸阳·七年级咸阳市实验中学校考阶段练习)如图,的顶点D,E在的边BC上,,,若,则的度数为( )
A.35° B.45° C.55° D.65°
题型五 与角平分线有关的三角形内角和问题
例题:(2023春·广东惠州·八年级校考期中)如图,在中,和分别平分和,若,则的大小为______ .
巩固训练
1.(2023·江苏扬州·校考二模)已知,如图,的的平分线和外角的平分线交于点,,,则_______°.
2.(2023春·广东惠州·八年级校考期中)如图,在中,是的平分线,,.求的度数.
3.(2023春·广东佛山·七年级校考期中)如图,在中,是的角平分线,作交于点E,,,求的度数.
题型六 三角形的外角的定义及性质
例题:(2023·陕西西安·校考模拟预测)如图,已知直线,被直线,所截,且,,,则的度数为( )
A. B. C. D.
巩固训练
1.(2023春·河南三门峡·七年级统考期中)为增强学生体质,感受中国的传统文化,学校将国家级非物质文化遗产“抖空竹”引入阳光特色大课间.如图是某同学“抖空竹”时的一个瞬间,王聪把它抽象成如图的数学问题:已知,,,则的度数为( ).
A. B. C. D.
2.(2023春·江苏泰州·七年级泰州市海军中学校考阶段练习)如图,若,,,则___________.
3.(2023·上海浦东新·校考三模)如图,已知,点A在上,点B和D在上,点C在的延长线上,,,则的度数是_____.
题型七 多边形的内角和与外角和
例题:(2023春·四川成都·八年级校考期中)一个多边形的内角和等于它的外角和的2倍,则这个多边形的边数是 .
巩固训练
1.(2023春·辽宁大连·七年级统考期中)如果一个多边形的内角和为,那么这个多边形是 边形.
2.(2023春·江苏泰州·七年级校考阶段练习)已知一个多边形的内角和与外角和之差为,则这个多边形的边数是 .
3.(2023春·海南省直辖县级单位·七年级校考阶段练习)(1)求出图中x的值
(2)若多边形的所有内角与它的一个外角的和为,求边数和内角和.
(3)如图,,,若,,求,,的度数.
题型八 在网格中画三角形的中线、高线及求三角形的面积
例题:(2023春·黑龙江哈尔滨·七年级哈尔滨市第六十九中学校校考期中)下图为的网格,每一小格均为正方形,已知.
(1)画出中边上的中线;
(2)画出中边上的高.
(3)直接写出的面积为_________.
巩固训练
1.(2023春·黑龙江哈尔滨·七年级哈尔滨市第四十七中学校考期中)如图所示方格纸中,每个小正方形的边长均为1,点A,点B,点C在小正方形的顶点上.
(1)画出中边上的高;
(2)画出中边上的中线;
(3)直接写出的面积为______.
2.(2023·全国·八年级假期作业)如图为的正方形网格,每个小正方形的边长均为1,已知△ABC的三个顶点均在格点上.按要求画图:
(1)画出△ABC的边BC上的高AD;
(2)连接格点,用一条线段将△ABC分成面积相等的两部分;
(3)直接写出△ABC的面积________.
【期中单元知识点归纳】(人教版)2023-2024学年七年级数学上册 第一章 有理数 试卷(知识归纳+八大题型突破): 这是一份【期中单元知识点归纳】(人教版)2023-2024学年七年级数学上册 第一章 有理数 试卷(知识归纳+八大题型突破),文件包含期中单元知识点归纳人教版2023-2024学年七年级数学上册第一章有理数知识归纳+八大题型突破原卷版docx、期中单元知识点归纳人教版2023-2024学年七年级数学上册第一章有理数知识归纳+八大题型突破解析版docx等2份试卷配套教学资源,其中试卷共32页, 欢迎下载使用。
【期中单元知识点归纳】(人教版)2023-2024学年七年级数学上册 第二章 整式的加减 试卷(知识归纳+题型突破): 这是一份【期中单元知识点归纳】(人教版)2023-2024学年七年级数学上册 第二章 整式的加减 试卷(知识归纳+题型突破),文件包含期中单元知识点归纳人教版2023-2024学年七年级数学上册第二章整式的加减知识归纳+题型突破原卷版docx、期中单元知识点归纳人教版2023-2024学年七年级数学上册第二章整式的加减知识归纳+题型突破解析版docx等2份试卷配套教学资源,其中试卷共30页, 欢迎下载使用。
【期中单元知识点归纳】(人教版)2023-2024学年九年级数学上册 第二十四章 圆试卷(知识归纳+题型突破): 这是一份【期中单元知识点归纳】(人教版)2023-2024学年九年级数学上册 第二十四章 圆试卷(知识归纳+题型突破),文件包含期中单元知识点归纳人教版2023-2024学年九年级数学上册第二十四章圆知识归纳+题型突破十一大题型176题原卷版docx、期中单元知识点归纳人教版2023-2024学年九年级数学上册第二十四章圆知识归纳+题型突破十一大题型176题解析版docx等2份试卷配套教学资源,其中试卷共209页, 欢迎下载使用。












