2024年新高考数学一轮复习题型归类与强化测试专题32平面向量的概念及线性运算（Word版附解析）

这是一份2024年新高考数学一轮复习题型归类与强化测试专题32平面向量的概念及线性运算（Word版附解析），共21页。试卷主要包含了【知识梳理】，【题型归类】，【培优训练】，【强化测试】等内容，欢迎下载使用。

专题32平面向量的概念及线性运算
知识梳理
考纲要求
考点预测
常用结论
方法技巧
题型归类
题型一：向量的基本概念
题型二：平面向量的线性运算
题型三：平面向量共线定理的应用

培优训练
训练一：
训练二：
训练三：
训练四：
训练五：
训练六：
强化测试
单选题：共8题
多选题：共4题
填空题：共4题
解答题：共6题
一、【知识梳理】
【考纲要求】
1.了解向量的实际背景.
2.理解平面向量的概念，理解两个向量相等的含义.
3.理解向量的几何表示.
4.掌握向量加法、减法的运算，并理解其几何意义.
5.掌握向量数乘的运算及其几何意义，理解两个向量共线的含义.
6.了解向量线性运算的性质及其几何意义.
【考点预测】
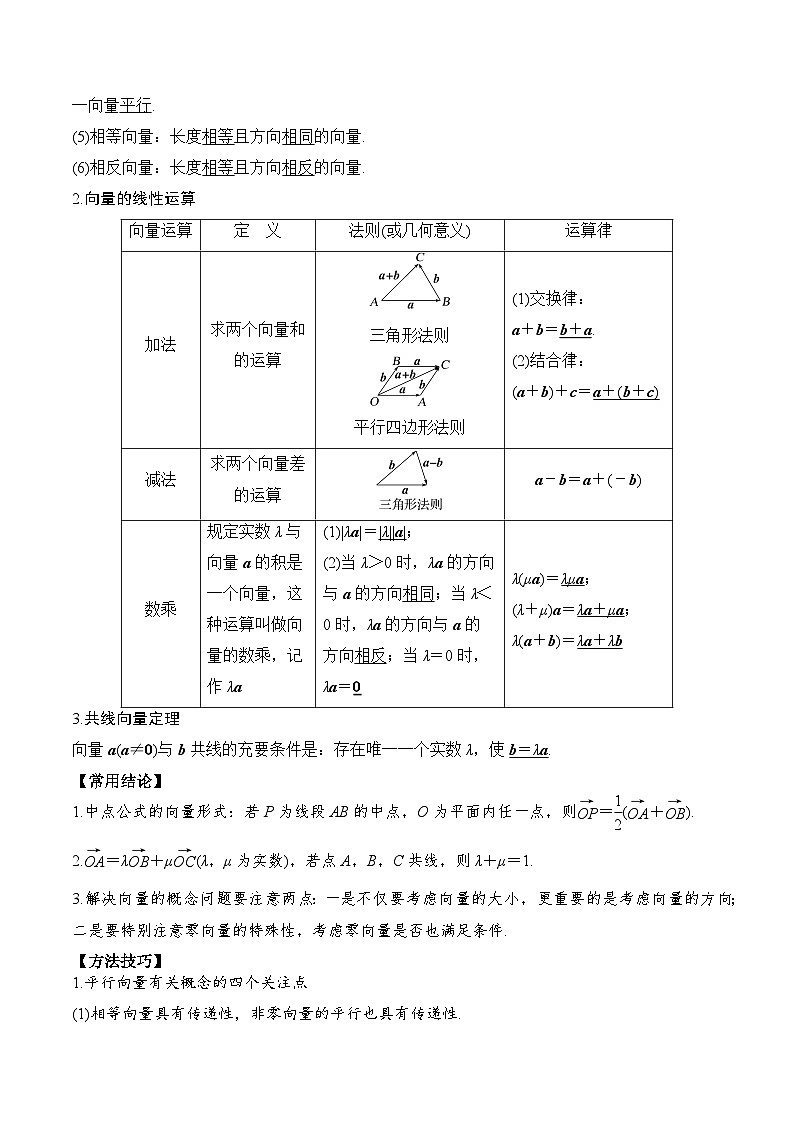
1.向量的有关概念
(1)向量：既有大小又有方向的量叫做向量，用有向线段表示，此时有向线段的方向就是向量的方向.向量的大小就是向量的长度(或称模)，记作||.
(2)零向量：长度为0的向量，记作0.
(3)单位向量：长度等于1个单位长度的向量.
(4)平行向量(共线向量)：方向相同或相反的非零向量.向量a，b平行，记作a∥b.规定：0与任一向量平行.
(5)相等向量：长度相等且方向相同的向量.
(6)相反向量：长度相等且方向相反的向量.
2.向量的线性运算
向量运算
定　义
法则(或几何意义)
运算律
加法
求两个向量和的运算

三角形法则

平行四边形法则
(1)交换律：
a＋b＝b＋a.
(2)结合律：
(a＋b)＋c＝a＋(b＋c)
减法
求两个向量差的运算

a－b＝a＋(－b)
数乘
规定实数λ与向量a的积是一个向量，这种运算叫做向量的数乘，记作λa
(1)|λa|＝|λ||a|；
(2)当λ＞0时，λa的方向与a的方向相同；当λ＜0时，λa的方向与a的方向相反；当λ＝0时，λa＝0
λ(μa)＝λμa；
(λ＋μ)a＝λa＋μa；
λ(a＋b)＝λa＋λb
3.共线向量定理
向量a(a≠0)与b共线的充要条件是：存在唯一一个实数λ，使b＝λa.
【常用结论】
1.中点公式的向量形式：若P为线段AB的中点，O为平面内任一点，则＝(＋).
2.＝λ＋μ(λ，μ为实数)，若点A，B，C共线，则λ＋μ＝1.
3.解决向量的概念问题要注意两点：一是不仅要考虑向量的大小，更重要的是考虑向量的方向；二是要特别注意零向量的特殊性，考虑零向量是否也满足条件.
【方法技巧】
1.平行向量有关概念的四个关注点
(1)相等向量具有传递性，非零向量的平行也具有传递性.
(2)共线向量即为平行向量，它们均与起点无关.
(3)向量可以平移，平移后的向量与原向量是相等向量，解题时，不要把它与函数图象的平移混淆.
(4)非零向量a与的关系：是与a同方向的单位向量.
2.(1)解决平面向量线性运算问题的关键在于熟练地找出图形中的相等向量，并能熟练运用相反向量将加减法相互转化.
(2)在求向量时要尽可能转化到平行四边形或三角形中，运用平行四边形法则、三角形法则及三角形中位线定理、相似三角形对应边成比例等平面几何的性质，把未知向量转化为用已知向量线性表示.
3.与向量的线性运算有关的参数问题，一般是构造三角形，利用向量运算的三角形法则进行加法或减法运算，然后通过建立方程组即可求得相关参数的值.
4.利用共线向量定理解题的策略
(1)a∥b⇔a＝λb(b≠0)是判断两个向量共线的主要依据.注意待定系数法和方程思想的运用.
(2)当两向量共线且有公共点时，才能得出三点共线，即A，B，C三点共线⇔，共线.
(3)若a与b不共线且λa＝μb，则λ＝μ＝0.
(4)＝λ＋μ(λ，μ为实数)，若A，B，C三点共线，则λ＋μ＝1.
二、【题型归类】
【题型一】向量的基本概念
【典例1】(多选)给出下列命题，不正确的有(　　)
A．若两个向量相等，则它们的起点相同，终点相同
B．若A，B，C，D是不共线的四点，且＝，则四边形ABCD为平行四边形
C．a＝b的充要条件是|a|＝|b|且a∥b
D．已知λ，μ为实数，若λa＝μb，则a与b共线
【解析】A错误，两个向量起点相同，终点相同，则两个向量相等，但两个向量相等，不一定有相同的起点和终点；
B正确，因为＝，所以||＝||且∥，又A，B，C，D是不共线的四点，所以四边形ABCD为平行四边形；
C错误，当a∥b且方向相反时，即使|a|＝|b|，也不能得到a＝b，所以|a|＝|b|且a∥b不是a＝b的充要条件，而是必要不充分条件；
D错误，当λ＝μ＝0时，a与b可以为任意向量，满足λa＝μb，但a与b不一定共线．
故选ACD.
【典例2】(多选)下列命题正确的是(　　)
A．零向量是唯一没有方向的向量
B．零向量的长度等于0
C．若a，b都为非零向量，则使＋＝0成立的条件是a与b反向共线
D．若a＝b，b＝c，则a＝c
【解析】A项，零向量是有方向的，其方向是任意的，故A错误；
B项，由零向量的定义知，零向量的长度为0，故B正确；
C项，因为与都是单位向量，所以只有当与是相反向量，即a与b是反向共线时才成立，故C正确；
D项，由向量相等的定义知D正确．
故选BCD.
【典例3】对于非零向量a，b，“a＋b＝0”是“a∥b”的(　　)
A．充分不必要条件
B．必要不充分条件
C．充要条件
D．既不充分也不必要条件
【解析】若a＋b＝0，
则a＝－b，则a∥b，即充分性成立；若a∥b，则a＝－b不一定成立，即必要性不成立，
即“a＋b＝0”是“a∥b”的充分不必要条件．
故选A.
【题型二】平面向量的线性运算
【典例1】设非零向量a，b满足|a＋b|＝|a－b|，则(　　)
A．a⊥b B．|a|＝|b|
C．a∥b D．|a|>|b|
【解析】方法一　利用向量加法的平行四边形法则．
在▱ABCD中，设＝a，＝b，
由|a＋b|＝|a－b|知，||＝||，
从而四边形ABCD为矩形，即AB⊥AD，故a⊥b.
故选A.
方法二　∵|a＋b|＝|a－b|，
∴|a＋b|2＝|a－b|2.
∴a2＋b2＋2a·b＝a2＋b2－2a·b.
∴a·b＝0.∴a⊥b.
故选A.
【典例2】在△ABC中，＝，若＝a，＝b，则等于(　　)
A.a＋b B.a＋b
C.a－b D.a－b
【解析】方法一　如图，过点D分别作AC，AB的平行线交AB，AC于点E，F，则四边形AEDF为平行四边形，所以＝＋.因为＝，所以＝，＝，所以＝＋＝a＋b，故选A.

方法二　＝＋＝＋＝＋(－)＝＋＝a＋b，故选A.
方法三　由＝，得－＝(－)，所以＝＋(－)＝＋＝a＋b.
故选A.
【典例3】在等腰梯形ABCD中，＝2，点E是线段的中点，若＝λ＋μ，则λ＋μ＝________.
【解析】取AB的中点F，连接CF，则由题意可得CF∥AD，且CF＝AD.因为＝＋＝＋＝＋(－)＝＋＝＋，所以λ＝，μ＝，则λ＋μ＝.
【题型三】平面向量共线定理的应用
【典例1】设两个非零向量a与b不共线．
(1)若＝a＋b，＝2a＋8b，＝3(a－b)，求证：A，B，D三点共线；
(2)试确定实数k，使ka＋b和a＋kb共线．
【解析】(1)证明：因为＝a＋b，＝2a＋8b，＝3(a－b)，
所以＝＋＝2a＋8b＋3(a－b)＝5(a＋b)＝5，
所以，共线，又它们有公共点B，
所以A，B，D三点共线．
(2)因为ka＋b与a＋kb共线，
所以存在实数λ，使ka＋b＝λ(a＋kb)，
即(k－λ)a＝(λk－1)b.
又a，b是两个不共线的非零向量，
所以k－λ＝λk－1＝0，所以k2－1＝0，
所以k＝±1.
【典例2】已知向量a与b不共线，＝a＋mb，＝na＋b(m，n∈R)，则与共线的条件是(　　)
A．m＋n＝0 B．m－n＝0
C．mn＋1＝0 D．mn－1＝0
【解析】由＝a＋mb，＝na＋b(m，n∈R)共线，得a＋mb＝λ(na＋b)，即所以mn－1＝0.
故选D.
【典例3】已知P是△ABC所在平面内的一点，若＝λ＋，其中λ∈R，则点P一定在(　　)
A．△ABC的内部 B．AC边所在直线上
C．AB边所在直线上 D．BC边所在直线上
【解析】由＝λ＋得－＝λ，＝λ.则，为共线向量，又，有一个公共点P，所以C，P，A三点共线，即点P在直线AC上．
故选B.
三、【培优训练】
【训练一】庄严美丽的国旗和国徽上的五角星是革命和光明的象征．正五角星是一个非常优美的几何图形，且与黄金分割有着密切的联系．在如图所示的正五角星中，以P，Q，R，S，T为顶点的多边形为正五边形，且＝.下列关系中正确的是(　　)

A.－＝ B．＋＝
C.－＝ D．＋＝
【解析】由已知，－＝－＝＝＝，所以A正确；
＋＝＋＝＝，所以B错误；
－＝－＝＝，所以C错误；
＋＝＋，＝＝－，若＋＝，则＝0，不合题意，所以D错误．
故选A.
【训练二】若2＋＋3＝0，S△AOC，S△ABC分别表示△AOC，△ABC的面积，则S△AOC∶S△ABC＝________.
【解析】若2＋＋3＝0，
设＝2，＝3，
可得O为△A′BC′的重心，如图，

设S△AOB＝x，S△BOC＝y，S△AOC＝z，
则S△A′OB＝2x，S△BOC′＝3y，S△A′OC′＝6z，
由2x＝3y＝6z，
可得S△AOC∶S△ABC＝z∶(x＋y＋z)＝1∶6.
【训练三】如图，在△ABC中，＝，P是BN上一点，若＝t＋，则实数t的值为________.
【解析】法一　因为＝，
所以＝，
所以＝t＋＝t＋，
因为B，P，N三点共线，
所以t＋＝1，所以t＝.
法二　因为＝，所以＝，
设＝λ，则＝＋
＝＋λ
＝＋λ(＋)
＝＋λ
＝λ＋(1－λ).
又＝t＋，
所以t＋＝λ＋(1－λ)，
得解得t＝λ＝.
【训练四】经过△OAB的重心G的直线与OA，OB分别交于点P，Q，设＝m，＝n，m，n∈R＋.
(1)证明：＋为定值；
(2)求m＋n的最小值.
【解析】(1)证明　设＝a，＝b.
由题意知＝×(＋)
＝(a＋b)，
＝－＝nb－ma，
＝－＝a＋b，
由P，G，Q三点共线得，
存在实数λ，使得＝λ，
即nb－ma＝λa＋λb，
从而
消去λ得＋＝3.
(2)解　由(1)知，＋＝3，
于是m＋n＝(m＋n)
＝≥(2＋2)＝.
当且仅当m＝n＝时，m＋n取得最小值，最小值为.
【训练五】经过△OAB的重心G的直线与OA，OB分别交于点P，Q，设＝m，＝n，m，n∈R*.
(1)证明：＋为定值；
(2)求m＋n的最小值．
【解析】(1)证明　设＝a，＝b.
由题意知＝×(＋)＝(a＋b)，
＝－＝nb－ma，
＝－＝a＋b，
由P，G，Q三点共线得，
存在实数λ，使得＝λ，
即nb－ma＝λa＋λb，
从而
消去λ得＋＝3.
(2)解　由(1)知，＋＝3，
于是m＋n＝(m＋n)
＝≥(2＋2)＝.
当且仅当m＝n＝时，m＋n取得最小值，最小值为.
【训练六】已知O，A，B是不共线的三点，且＝m＋n(m，n∈R)．
(1)若m＋n＝1，求证：A，P，B三点共线；
(2)若A，P，B三点共线，求证：m＋n＝1.
【证明】(1)若m＋n＝1，
则＝m＋(1－m)
＝＋m(－)，
所以－＝m(－)，
即＝m，所以与共线．
又因为与有公共点B，
所以A，P，B三点共线．
(2)若A，P，B三点共线，
则存在实数λ，使＝λ，所以－＝λ(－)．
又＝m＋n.
故有m＋(n－1)＝λ－λ，
即(m－λ)＋(n＋λ－1)＝0.
因为O，A，B不共线，所以，不共线，
所以所以m＋n＝1.
四、【强化测试】
【单选题】
1. 若a，b为非零向量，则“＝”是“a，b共线”的(　　)
A．充要条件
B．充分不必要条件
C．必要不充分条件
D．既不充分也不必要条件
【解析】，分别表示与a，b同方向的单位向量，＝，则有a，b共线，而a，b共线，则，是相等向量或相反向量，所以“＝”是“a，b共线”的充分不必要条件．
故选B.
2. 设a＝(＋)＋(＋)，b是一个非零向量，则下列结论不正确的是(　　)
A．a∥b B．a＋b＝a
C．a＋b＝b D．|a＋b|＝|a|＋|b|
【解析】由题意得，a＝(＋)＋(＋)＝＋＝0，且b是一个非零向量，所以a∥b成立，所以A正确；由a＋b＝b，所以B不正确，C正确；由|a＋b|＝|b|，|a|＋|b|＝|b|，
所以|a＋b|＝|a|＋|b|，所以D正确．
故选B.
3. 如图所示，在正六边形ABCDEF中，＋＋等于(　　)

A．0 B.
C. D.
【解析】根据正六边形的性质，
易得，＋＋
＝＋＋
＝＋＝.
故选D.
4. 已知平面内一点P及△ABC，若＋＋＝，则点P与△ABC的位置关系是(　　)
A．点P在线段AB上 B．点P在线段BC上
C．点P在线段AC上 D．点P在△ABC外部
【解析】由＋＋＝，得＋＋＝－，即＝－2，故点P在线段AC上．
故选C.
5. 已知O是正方形ABCD的中心．若＝λ＋μ，其中λ，μ∈R，则＝(　　)
A．－2 B．－
C．－ D．
【解析】＝＋＝＋＝－＋＝AB－，所以λ＝1，μ＝－，因此＝－2.
故选A.
6. 矩形ABCD的对角线相交于点O，E为AO的中点，若＝λ＋μ(λ，μ为实数)，则λ2＋μ2＝(　　)
A. B. C.1 D.
【解析】＝－＝－
＝(＋)－＝－，
∴λ＝，μ＝－.∴λ2＋μ2＝＋＝.
故选A.
7. 在△ABC中，点M为AC上的点，且＝，若＝λ＋μ，则λ－μ的值是(　　)
A.1 B. C. D.
【解析】由＝，得＝，所以＝＋＝＋＝＋(－)＝＋，又因为＝λ＋μ，所以λ＝，μ＝，故λ－μ＝.
故选C.
8. 如图，在平行四边形ABCD中，E为BC的中点，F为DE的中点，若＝x＋，则x等于(　　)

A. B.
C. D.
【解析】连接AE(图略)，因为F为DE的中点，
所以＝(＋)，
而＝＋＝＋＝＋，
所以＝(＋)
＝
＝＋，
又＝x＋，
所以x＝.
故选C.
【多选题】
9. 下列选项中的式子，结果为零向量的是(　　)
A.＋＋
B.＋＋＋
C.＋＋＋
D.－＋－
【解析】利用向量运算，易知A，D中的式子结果为零向量．
故选AD.
10. (多选)下列说法中正确的是(　　)
A.＋＝0
B．若|a|＝|b|且a∥b，则a＝b
C．向量a与b不共线，则a与b都是非零向量
D．若a∥b，则有且只有一个实数λ，使得b＝λa
【解析】由，互为相反向量，得＋＝0，故A正确；
由|a|＝|b|且a∥b，得a＝b或a＝－b，故B错误；
若a与b不共线，则a与b都是非零向量，故C正确；
根据向量共线基本定理可知D错误，因为要排除零向量．
故选AC.
11. (多选)设点M是△ABC所在平面内一点，则下列说法正确的是(　　)
A．若＝＋，则点M是边BC的中点
B．若＝2－，则点M在边BC的延长线上
C．若＝－－，则点M是△ABC的重心
D．若＝x＋y，且x＋y＝，则△MBC的面积是△ABC面积的
【解析】若＝＋，则点M是边BC的中点，故A正确；
若＝2－，即有－＝－，
即＝，
则点M在边CB的延长线上，故B错误；
若＝－－，
即＋＋＝0，
则点M是△ABC的重心，故C正确；
如图，＝x＋y，

且x＋y＝，
可得2＝2x＋2y，
设＝2，
则M为AN的中点，
则△MBC的面积是△ABC面积的，故D正确．
故选ACD.
12. 点P是△ABC所在平面内一点，且满足|－|－|＋－2|＝0，则△ABC不可能是(　　)
A．钝角三角形 B．直角三角形
C．等腰三角形 D．等边三角形
【解析】因为点P是△ABC所在平面内一点，且|－|－|＋－2|＝0，
所以||－|(－)＋(－)|＝0，
即||＝|＋|，
所以|－|＝|＋|，
等式两边平方并化简得·＝0，
所以⊥，∠BAC＝90°，则△ABC一定是直角三角形，也有可能是等腰直角三角形，不可能是钝角三角形和等边三角形．
故选AD.
【填空题】
13. 若||＝||＝|－|＝2，则|＋|＝________．
【解析】因为||＝||＝|－|＝||＝2，
所以△ABC是边长为2的正三角形，
所以|＋|为△ABC的边BC上的高的2倍，
所以|＋|＝2.
14. 已知e1，e2为平面内两个不共线的向量，＝2e1－3e2，＝λe1＋6e2，若M，N，P三点共线，则λ＝________．
【解析】因为M，N，P三点共线，
所以存在实数k使得＝k，
所以2e1－3e2＝k(λe1＋6e2)，
又e1，e2为平面内两个不共线的向量，
可得解得λ＝－4.
15. 已知▱ABCD的对角线AC和BD相交于点O，且＝a，＝b，则＝________，＝________．(用a，b表示)
【解析】如图，＝＝－＝b－a，＝－＝－－＝－a－b.

16. 在直角梯形ABCD中，∠A＝90°，∠B＝30°，AB＝2，BC＝2，点E在线段CD上，若＝＋μ，则μ的取值范围是________．
【解析】由已知AD＝1，CD＝，所以＝2.
因为点E在线段CD上，所以＝λ(0≤λ≤1)．
因为＝＋，
又＝＋μ＝＋2μ＝＋，
所以＝1，即μ＝.
因为0≤λ≤1，所以0≤μ≤.
【解答题】
17. 在△ABC中，D，E分别为BC，AC边上的中点，G为BE上一点，且GB＝2GE，设＝a，＝b，试用a，b表示，.

【解析】＝(＋)＝a＋b；
＝＋＝＋＝＋(＋)＝＋(－)＝＋＝a＋b.
18. 已知O，A，B是不共线的三点，且＝m＋n(m，n∈R)．
(1)若m＋n＝1，求证：A，P，B三点共线；
(2)若A，P，B三点共线，求证：m＋n＝1.
【解析】证明：(1)若m＋n＝1，
则＝m＋(1－m)
＝＋m(－)，
所以－＝m(－)，
即＝m，所以与共线．
又因为与有公共点B，
所以A，P，B三点共线．
(2)若A，P，B三点共线，
则存在实数λ，使＝λ，所以－＝λ(－)．
又＝m＋n.
故有m＋(n－1)＝λ－λ，
即(m－λ)＋(n＋λ－1)＝0.
因为O，A，B三点不共线，所以，不共线，
所以所以m＋n＝1.
19. 已知a，b不共线，＝a，＝b，＝c，＝d，＝e，设t∈R，如果3a＝c,2b＝d，e＝t(a＋b)，是否存在实数t使C，D，E三点在一条直线上？若存在，求出实数t的值，若不存在，请说明理由．
【解析】由题设知，＝d－c＝2b－3a，
＝e－c＝(t－3)a＋tb，
C，D，E三点在一条直线上的充要条件是存在实数k，使得＝k，
即(t－3)a＋tb＝－3ka＋2kb，
整理得(t－3＋3k)a＝(2k－t)b.
因为a，b不共线，
所以有解得t＝.
故存在实数t＝使C，D，E三点在一条直线上．
20. 如图，在△ABC中，D为BC的四等分点，且靠近B点，E，F分别为AC，AD的三等分点，且分别靠近A，D两点，设＝a，＝b.

(1)试用a，b表示，，；
(2)证明：B，E，F三点共线．
【解析】(1)解　在△ABC中，因为＝a，＝b，
所以＝－＝b－a，
＝＋＝＋
＝a＋(b－a)＝a＋b，
＝＋＝－＋＝－a＋b.
(2)证明　因为＝－a＋b，
＝＋＝－＋
＝－a＋＝－a＋b
＝，
所以＝，与共线，且有公共点B，
所以B，E，F三点共线．
21. 设两向量a与b不共线.
(1)若＝a＋b，＝2a＋8b，＝3(a－b).求证：A，B，D三点共线；
(2)试确定实数k，使ka＋b和a＋kb共线.
【解析】(1)证明　∵＝a＋b，＝2a＋8b，＝3(a－b).
∴＝＋＝2a＋8b＋3(a－b)＝2a＋8b＋3a－3b＝5(a＋b)＝5.
∴，共线，又它们有公共点B，
∴A，B，D三点共线.
(2)解　∵ka＋b与a＋kb共线，
∴存在实数λ，
使ka＋b＝λ(a＋kb)，即ka＋b＝λa＋λkb，
∴(k－λ)a＝(λk－1)b.
∵a，b是不共线的两个向量，
∴k－λ＝λk－1＝0，∴k2－1＝0，∴k＝±1.
22. 如图，EF是等腰梯形ABCD的中位线，M，N是EF上的两个三等分点，若＝a，＝b，＝2.

(1)用a，b表示；
(2)证明：A，M，C三点共线．
【解析】(1)＝＋＋
＝a＋b＋＝a＋b，
又E为AD的中点，
所以＝＝a＋b，
因为EF是梯形ABCD的中位线，且＝2，
所以＝(＋)＝＝a，
又M，N是EF的三等分点，
所以＝＝a，
所以＝＋＝a＋b＋a
＝a＋b.
(2)证明：由(1)知＝＝a，
所以＝＋＝a＋b＝，
又与有公共点M，所以A，M，C三点共线．