初中数学北京课改版八年级上册12.2 三角形的性质教案配套ppt课件

这是一份初中数学北京课改版八年级上册12.2 三角形的性质教案配套ppt课件，共16页。PPT课件主要包含了等边对等角，三线合一，等角对等边，两边相等，两腰相等，轴对称图形，知识回顾，等边三角形，正三角形，学习园地等内容，欢迎下载使用。

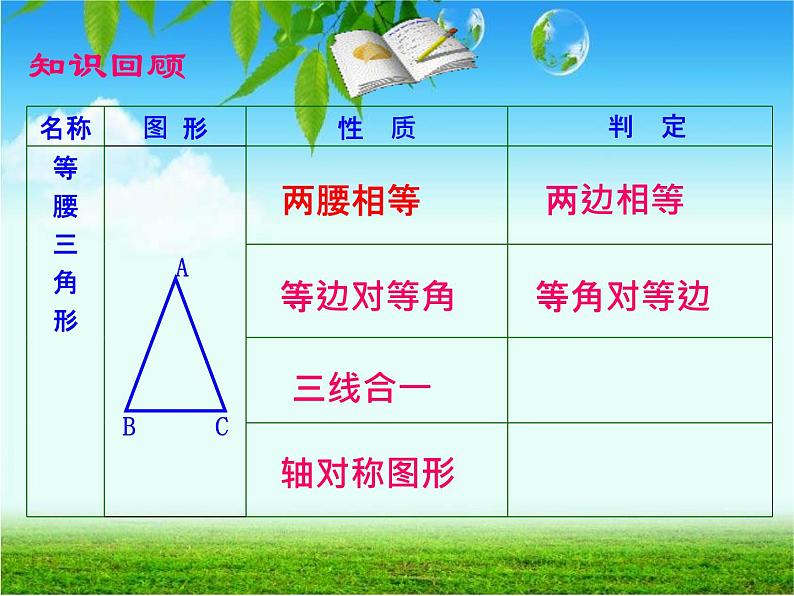
三条边都相等的三角形.
等边三角形是特殊的等腰三角形.
把等腰三角形的性质用于等边三角形，能得到什么结论？
一个三角形的三个内角满足什么条件才是等边三角形
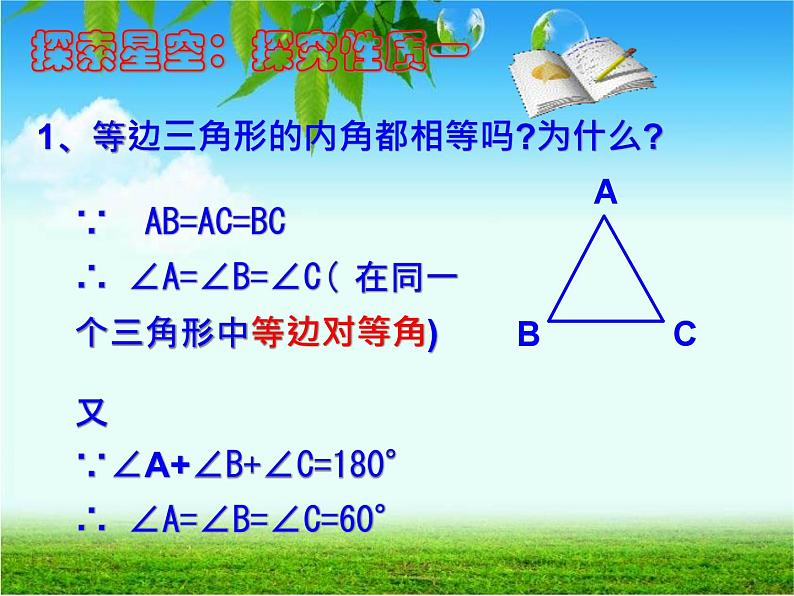
1、等边三角形的内角都相等吗?为什么?
∵ AB=AC=BC∴ ∠A=∠B=∠C(在同一个三角形中等边对等角)
又∵∠A+∠B+∠C=180°∴ ∠A=∠B=∠C=60°
等边三角形的内角都相等，并且每一个内角都等于60°.
如何用符号语言来表达呢?
∵ △ABC是等边三角形∴ ∠A=∠B=∠C=60°
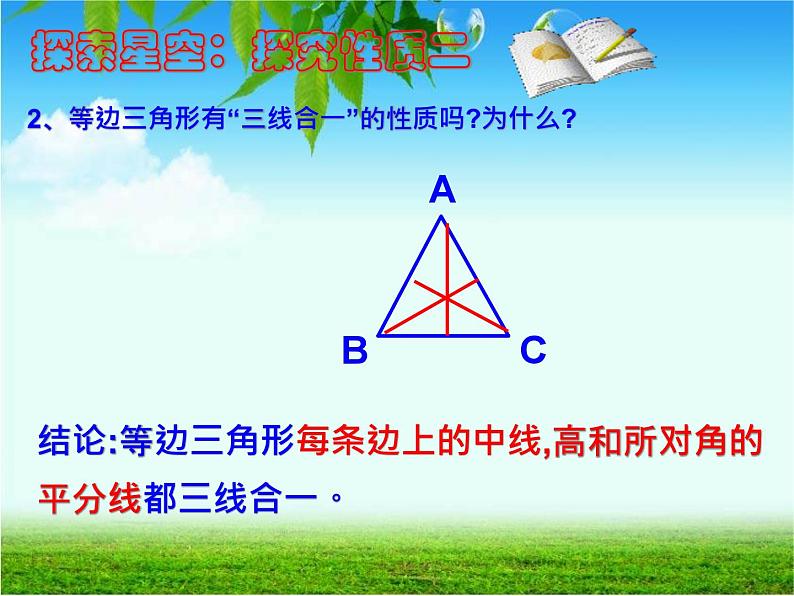
2、等边三角形有“三线合一”的性质吗?为什么?
结论:等边三角形每条边上的中线,高和所对角的平分线都三线合一。
3、等边三角形是轴对称图形吗?有几条对称轴?
2.等边三角形的内角都相等,且等于60 °
3.等边三角形各边上中线,高和所对角的平分线都三线合一.
4.等边三角形是轴对称图形，有三条对称轴. 中线（角平分线，高）所在的直线就是它的对称轴。
∵ ∠A=∠B=∠C∴ AB=AC=BC (在同一个三角形中等角对等边)
1、三个内角都相等的三角形是等边三角形。
∴ △ABC是等边三角形
2、有一个内角是60°的等腰三角形是等边三角形。
当顶角为60°时，两个底角各为60°.
当底角为60°时，顶角为60°.
等边三角形的判定方法:
1.三边相等的三角形是等边三角形.
2.三个内角都相等的三角形是等边三角形.
3.有一个内角是60 °的等腰三角形是等边三角形.
例4，课本(P80),如图：△ABC是等边三角形，DE∥BC,分别交AB，AC于点D，E. 求证：△ADE是等边三角形
∵△ABC是等边三角形
∴ ∠ADE=∠B, ∠AED=∠C
∴ ∠A=∠ADE=∠AED
∴ △ ADE是等边三角形
想一想，本题还有其他证法吗？
　１、下列四个说法中，不正确的有（ ）　　　（A）0个（B）1个（C）2个（D）3个三个角都相等的三角形是等边三角形。有两个角等于60°的三角形是等边三角形。有一个是60°的等腰三角形是等边三角形。有两个角相等的等腰三角形是等边三角形。２、等边三角形的对称轴有（ ）　　（A）1条（B）2条（C）3条（D）4条　　３、等边三角形中，高、中线、角平分线共有（ ）　　（A）3条（B）6条（C）9条（D）7条 
1、如图，在等边三角形ABC中AD⊥BC于D。以AD为一边，作等边三角形ADE，则DE与AC垂直吗？请说明理由。
2：如图，△ABC是等边三角形，P、Q分别是AC、BC上的 点，且AP=CQ，AQ与BP交于点M。求∠BMQ的度数。