
2019年江苏省徐州市中考数学试卷-(4年中考)
展开2019年江苏省徐州市中考数学试卷-(4年中考)
一、选择题(本大题共有8小题,每小题3分,共24分)
1.﹣2的倒数是( )
A.﹣ B. C.2 D.﹣2
2.下列计算正确的是( )
A.a2+a2=a4 B.(a+b)2=a2+b2 C.(a3)3=a9 D.a3•a2=a6
3.下列长度的三条线段,能组成三角形的是( )
A.2,2,4 B.5,6,12 C.5,7,2 D.6,8,10
4.抛掷一枚质地均匀的硬币2000次,正面朝上的次数最有可能为( )
A.500 B.800 C.1000 D.1200
5.某小组7名学生的中考体育分数如下:37,40,39,37,40,38,40,该组数据的众数、中位数分别为( )
A.40,37 B.40,39 C.39,40 D.40,38
6.下图均由正六边形与两条对角线所组成,其中不是轴对称图形的是( )
A. B. C. D.
7.若A(x1,y1)、B(x2,y2)都在函数y=的图象上,且x1<0<x2,则( )
A.y1<y2 B.y1=y2 C.y1>y2 D.y1=﹣y2
8.如图,数轴上有O、A、B三点,O为原点,OA、OB分别表示仙女座星系、M87黑洞与地球的距离(单位:光年).下列选项中,与点B表示的数最为接近的是( )
A.5×106 B.107 C.5×107 D.108
二、填空題(本大题共有10小题,每小题3分,共30分.)
9.8的立方根是 .
10.使有意义的x的取值范围是 .
11.方程x2﹣4=0的解是 .
12.若a=b+2,则代数式a2﹣2ab+b2的值为 .
13.如图,矩形ABCD中,AC、BD交于点O,M、N分别为BC、OC的中点.若MN=4,则AC的长为 .
14.如图,A、B、C、D为一个外角为40°的正多边形的顶点.若O为正多边形的中心,则∠OAD= .
15.如图,沿一条母线将圆锥侧面剪开并展平,得到一个扇形,若圆锥的底面圆的半径r=2cm,扇形的圆心角θ=120°,则该圆锥的母线长l为 cm.
16.如图,无人机于空中A处测得某建筑顶部B处的仰角为45°,测得该建筑底部C处的俯角为17°.若无人机的飞行高度AD为62m,则该建筑的高度BC为 m.
(参考数据:sin17°≈0.29,cos17°≈0.96,tan17°≈0.31)
17.已知二次函数的图象经过点P(2,2),顶点为O(0,0)将该图象向右平移,当它再次经过点P时,所得抛物线的函数表达式为 .
18.函数y=x+1的图象与x轴、y轴分别交于A、B两点,点C在x轴上.若△ABC为等腰三角形,则满足条件的点C共有 个.
三、解答题(本大题共有10小题,共86分)
19.(10分)计算:
(1)π0﹣+()﹣2﹣|﹣5|; (2)÷.
20.(10分)(1)解方程:+1= (2)解不等式组:
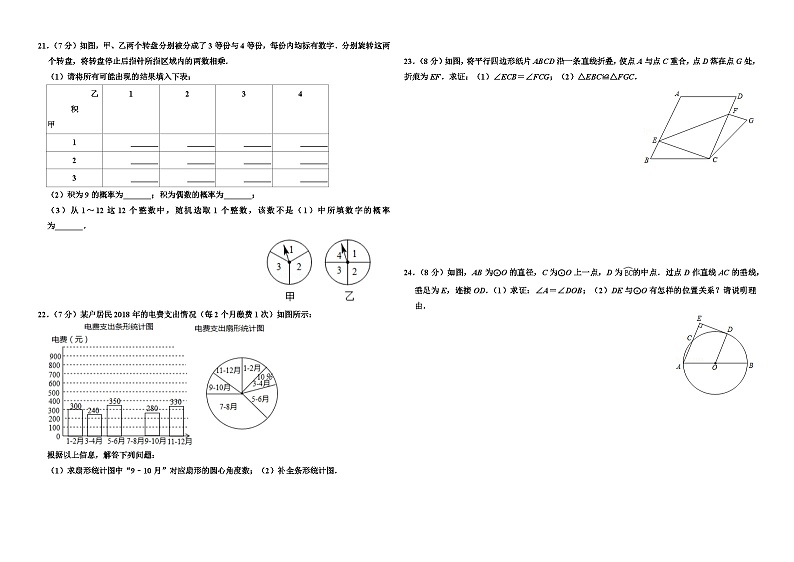
21.(7分)如图,甲、乙两个转盘分别被分成了3等份与4等份,每份内均标有数字.分别旋转这两个转盘,将转盘停止后指针所指区域内的两数相乘.
(1)请将所有可能出现的结果填入下表:
乙
积
甲
1
2
3
4
1
2
3
(2)积为9的概率为 ;积为偶数的概率为 ;
(3)从1~12这12个整数中,随机选取1个整数,该数不是(1)中所填数字的概率为 .
22.(7分)某户居民2018年的电费支出情况(每2个月缴费1次)如图所示:
根据以上信息,解答下列问题:
(1)求扇形统计图中“9﹣10月”对应扇形的圆心角度数;(2)补全条形统计图.
23.(8分)如图,将平行四边形纸片ABCD沿一条直线折叠,使点A与点C重合,点D落在点G处,折痕为EF.求证:(1)∠ECB=∠FCG;(2)△EBC≌△FGC.
24.(8分)如图,AB为⊙O的直径,C为⊙O上一点,D为的中点.过点D作直线AC的垂线,垂足为E,连接OD.(1)求证:∠A=∠DOB;(2)DE与⊙O有怎样的位置关系?请说明理由.
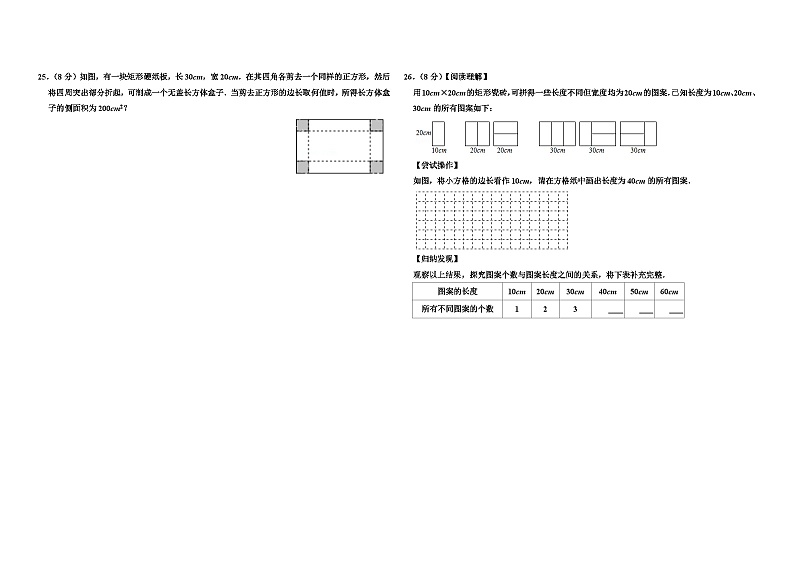
25.(8分)如图,有一块矩形硬纸板,长30cm,宽20cm.在其四角各剪去一个同样的正方形,然后将四周突出部分折起,可制成一个无盖长方体盒子.当剪去正方形的边长取何值时,所得长方体盒子的侧面积为200cm2?
26.(8分)【阅读理解】
用10cm×20cm的矩形瓷砖,可拼得一些长度不同但宽度均为20cm的图案.已知长度为10cm、20cm、30cm的所有图案如下:
【尝试操作】
如图,将小方格的边长看作10cm,请在方格纸中画出长度为40cm的所有图案.
【归纳发现】
观察以上结果,探究图案个数与图案长度之间的关系,将下表补充完整.
图案的长度
10cm
20cm
30cm
40cm
50cm
60cm
所有不同图案的个数
1
2
3
27.(9分)如图①,将南北向的中山路与东西向的北京路看成两条直线,十字路口记作点A.甲从中山路上点B出发,骑车向北匀速直行;与此同时,乙从点A出发,沿北京路步行向东匀速直行.设出发xmin时,甲、乙两人与点A的距离分别为y1m、y2m.已知y1、y2与x之间的函数关系如图②所示.(1)求甲、乙两人的速度;(2)当x取何值时,甲、乙两人之间的距离最短?
28.(11分)如图,平面直角坐标系中,O为原点,点A、B分别在y轴、x轴的正半轴上.△AOB的两条外角平分线交于点P,P在反比例函数y=的图象上.PA的延长线交x轴于点C,PB的延长线交y轴于点D,连接CD.
(1)求∠P的度数及点P的坐标;(2)求△OCD的面积;
(3)△AOB的面积是否存在最大值?若存在,求出最大面积;若不存在,请说明理由.
2019年江苏省徐州市中考数学试卷答案
1. A.2. C.3. D.4. C.5. B.6. D.7. A.8. D.
9. 2.10. x≥﹣1.11.±2.12. 413. 16.14. 140°15. 6.16. 262.17. y=(x﹣4)2.18. 3;
19.解:(1)原式=1﹣3+9﹣5=2;
(2)原式=÷
=(x﹣4)•
=2x.
20.解:(1)+1=,
两边同时乘以x﹣3,得
x﹣2+x﹣3=﹣2,
∴x=;
经检验x=是原方程的根;
(2)由可得,
∴不等式的解为﹣2<x≤2;
21.解:(1)补全表格如下:
1
2
3
4
1
1
2
3
4
2
2
4
6
8
3
3
6
9
12
(2)由表知,共有12种等可能结果,其中积为9的有1种,积为偶数的有8种结果,
所以积为9的概率为;积为偶数的概率为=,
故答案为:,.
(3)从1~12这12个整数中,随机选取1个整数,该数不是(1)中所填数字的有5和7这2种,
∴此事件的概率为=,
故答案为:.
22.解:(1)全年的总电费为:240÷10%=2400元
9﹣10月份所占比:280÷2400=,
∴扇形统计图中“9﹣10月”对应扇形的圆心角度数为:360°×=42°
答:扇形统计图中“9﹣10月”对应扇形的圆心角度数是42°
(2)7﹣8月份的电费为:2400﹣300﹣240﹣350﹣280﹣330=900元,
补全的统计图如图:
23.证明:(1)∵四边形ABCD是平行四边形,
∴∠A=∠BCD,
由折叠可得,∠A=∠ECG,
∴∠BCD=∠ECG,
∴∠BCD﹣∠ECF=∠ECG﹣∠ECF,
∴∠ECB=∠FCG;
(2)∵四边形ABCD是平行四边形,
∴∠D=∠B,AD=BC,
由折叠可得,∠D=∠G,AD=CG,
∴∠B=∠G,BC=CG,
又∵∠ECB=∠FCG,
∴△EBC≌△FGC(ASA).
24.(1)证明:连接OC,
∵D为的中点,
∴=,
∴∠BCD=BOC,
∵∠BAC=BOC,
∴∠A=∠DOB;
(2)解:DE与⊙O相切,
理由:∵∠A=∠DOB,
∴AE∥OD,
∵DE⊥AE,
∴OD⊥DE,
∴DE与⊙O相切.
25.解:设剪去正方形的边长为xcm,则做成无盖长方体盒子的底面长为(30﹣2x)cm,宽为(20﹣2x)cm,高为xcm,
依题意,得:2×[(30﹣2x)+(20﹣2x)]x=200,
整理,得:2x2﹣25x+50=0,
解得:x1=,x2=10.
当x=10时,20﹣2x=0,不合题意,舍去.
答:当剪去正方形的边长为cm时,所得长方体盒子的侧面积为200cm2.
26.解:如图:
根据作图可知40cm时,所有图案个数4个;
50cm时,所有图案个数5个;
60cm时,所有图案个数6个;
故答案为4,5,6;
27.解:(1)设甲、乙两人的速度分别为am/min,bm/min,则:
y1=
y2=bx
由图②知:x=3.75或7.5时,y1=y2,∴,解得:
答:甲的速度为240m/min,乙的速度为80m/min.
(2)设甲、乙之间距离为d,
则d2=(1200﹣240x)2+(80x)2
=64000(x﹣)2+144000,
∴当x=时,d2的最小值为144000,即d的最小值为120;
答:当x=时,甲、乙两人之间的距离最短.
28.解:(1)如图,作PM⊥OAYM,PN⊥OB于N,PH⊥AB于H.
∴∠PMA=∠PHA=90°,
∵∠PAM=∠PAH,PA=PA,
∴△PAM≌△PAH(AAS),
∴PM=PH,∠APM=∠APH,
同理可证:△BPN≌△BPH,
∴PH=PN,∠BPN=∠BPH,
∴PM=PN,
∵∠PMO=∠MON=∠PNO=90°,
∴四边形PMON是矩形,
∴∠MPN=90°,
∴∠APB=∠APH+∠BPH=(∠MPH+∠NPH)=45°,
∵PM=PN,
∴可以假设P(m,m),
∵P(m,m)在y=上,
∴m2=9,
∵m>0,
∴m=3,
∴P(3,3).
(2)设OA=a,OB=b,则AM=AH=3﹣a,BN=BH=3﹣b,
∴AB=6﹣a﹣b,
∵AB2=OA2+OB2,
∴a2+b2=(6﹣a﹣b)2,
可得ab=18﹣6a﹣6b,
∴9﹣3a﹣3b=ab,
∵PM∥OC,
∴=,
∴=,
∴OC=,同法可得OD=,
∴S△COD=•OC•DO====6.
(3)设OA=a,OB=b,则AM=AH=3﹣a,BN=BH=3﹣b,
∴AB=6﹣a﹣b,
∴OA+OB+AB=6,
∴a+b+=6,
∴2+≤6,
∴(2+)≤6,
∴≤3(2﹣),
∴ab≤54﹣36,
∴S△AOB=ab≤27﹣18,
∴△AOB的面积的最大值为27﹣18.
2016年徐州市中考数学试卷
一、选择题:本大题共8小题,每小题3分,共24分
1.﹣的相反数是( )
A.4 B.﹣4 C. D.﹣
2.下列运算中,正确的是( )
A.x2+x3=x6 B.x3+x9=x27 C.(x2)3=x6 D.x÷x2=x3
3.下列事件中的不可能事件是( )
A.通常加热到100℃时,水沸腾 B.抛掷2枚正方体骰子,都是6点朝上
C.经过有交通信号灯的路口,遇到红灯 D.任意画一个三角形,其内角和是360°
4.下列图形中,不可以作为一个正方体的展开图的是( )
A. B. C. D.
5.下列图案中,是轴对称图形但不是中心对称图形的是( )
A. B. C. D.
6.某人一周内爬楼的层数统计如表
周一
周二
周三
周四
周五
周六
周日
26
36
22
22
24
31
21
关于这组数据,下列说法错误的是( )
A.中位数是22 B.平均数是26 C.众数是22 D.极差是15
7.函数y=中自变量x的取值范围是( )
A.x≤2 B.x≥2 C.x<2 D.x≠2
8.如图是由三个边长分别为6、9、x的正方形所组成的图形,若直线AB将它分成面积相等的两部分,则x的值是( )
A.1或9 B.3或5 C.4或6 D.3或6
(第13题图) (第15题图)
二、填空题:本大题共10小题,每小题3分,共30分
9.9的平方根是______.
10.某市2016年中考考生约为61500人,该人数用科学记数法表示为______.
11.若反比例函数的图象过点(3,﹣2),则其函数表达式为______.
12.若二次函数y=x2+2x+m的图象与x轴没有公共点,则m的取值范围是______.
13.如图,△ABC中,D、E分别为AB、AC的中点,则△ADE与△ABC的面积比为______.
14.若等腰三角形的顶角为120°,腰长为2cm,则它的底边长为______cm.
15.如图,⊙O是△ABC的内切圆,若∠ABC=70°,∠ACB=40°,则∠BOC=______°.
16.用一个半径为10的半圆,围成一个圆锥的侧面,该圆锥的底面圆的半径为______.
17.如图,每个图案都由大小相同的正方形组成,按照此规律,第n个图案中这样的正方形的总个数可用含n的代数式表示为______.
18.如图,正方形ABCD的边长为2,点E,F分别在边AD,CD上,若∠EBF=45°,则△EDF的周长等于______.
三、解答题:本大题共10小题,共86分
19.(10分)计算:
(1)(﹣1)2016+x0﹣+ (2)÷.
20.(10分)(1)解方程:+1=; (2)解不等式组:.
21.(7分)某校随机抽取部分学生,就“学习习惯”进行调查,将“对自己做错的题目进行整理、分析、改正”(选项为:很少、有时、常常、总是)的调查数据进行了整理,绘制成部分统计图如下:
请根据图中信息,解答下列问题
(1)该调查的样本容量为______,a=______%,b=______%,“常常”对应扇形的圆心角为______°
(2)请你补全条形统计图;
(3)若该校共有3200名学生,请你估计其中“总是”对错题进行整理、分析、改正的学生有多少名?
22.(7分)某乳品公司最近推出一款果味酸奶,共有红枣、木瓜两种口味,若送奶员连续三天,每天从中任选一瓶某种口味的酸奶赠送给某住户品尝,则该住户收到的三瓶酸奶中,至少有两瓶为红枣口味的概率是多少?
(请用“画树状图”的方法给出分析过程,并求出结果)
23.(8分)如图,在△ABC中,∠ABC=90°,∠BAC=60°,△ACD是等边三角形,E是AC的中点,连接BE并延长,交DC于点F,求证:
(1)△ABE≌△CFE;(2)四边形ABFD是平行四边形.
24.(8分)小丽购买学习用品的收据如表,因污损导致部分数据无法识别,根据下表,解决下列问题:
(1)小丽买了自动铅笔、记号笔各几支?
(2)若小丽再次购买软皮笔记本和自动铅笔两种文具,共花费15元,则有哪几种不同的购买方案?
商品名
单价(元)
数量(个)
金额(元)
签字笔
3
2
6
自动铅笔
1.5
●
●
记号笔
4
●
●
软皮笔记本
●
2
9
圆规
3.5
1
●
合计
8
28
25.(8分)如图,为了测出旗杆AB的高度,在旗杆前的平地上选择一点C,测得旗杆顶部A的仰角为45°,在C、B之间选择一点D(C、D、B三点共线),测得旗杆顶部A的仰角为75°,且CD=8m
(1)求点D到CA的距离;
(2)求旗杆AB的高.
(注:结果保留根号)
26.(8分)某宾馆拥有客房100间,经营中发现:每天入住的客房数y(间)与其价格x(元)(180≤x≤300)满足一次函数关系,部分对应值如表:
x(元)
180
260
280
300
y(间)
100
60
50
40
(1)求y与x之间的函数表达式;
(2)已知每间入住的客房,宾馆每日需支出各种费用100元;每日空置的客房需支出各种费用60元,当房价为多少元时,宾馆当日利润最大?求出最大值.(宾馆当日利润=当日房费收入﹣当日支出)
27.(9分)如图,将边长为6的正方形纸片ABCD对折,使AB与DC重合,折痕为EF,展平后,再将点B折到边CD上,使边AB经过点E,折痕为GH,点B的对应点为M,点A的对应点为N
(1)若CM=x,则CH=______(用含x的代数式表示);
(2)求折痕GH的长.
28.(11分)如图,在平面直角坐标系中,二次函数y=ax2+bx+c的图象经过点A(﹣1,0),B(0,﹣),C(2,0),其对称轴与x轴交于点D
(1)求二次函数的表达式及其顶点坐标;
(2)若P为y轴上的一个动点,连接PD,则PB+PD的最小值为______;
(3)M(x,t)为抛物线对称轴上一动点
①若平面内存在点N,使得以A,B,M,N为顶点的四边形为菱形,则这样的点N共有______个;
②连接MA,MB,若∠AMB不小于60°,求t的取值范围.
2016年徐州市中考数学试卷答案
1. C.2. C.3. D.4. C.5. B.6. A.7. A.8. D.
9.±3. 10. 6.15×104.11. y=﹣.12. m>1.13. 1:4.14. 2.15. 125.16. 5
17. n(n+1).18. 4.
19.解:(1)原式=1+1﹣3+2=1;
(2)原式=×=x.
20.解:(1)去分母,得:x﹣3+x﹣2=﹣3,
整理,得:2x=2,
∴x=1.
经检验,x=1是原方程得解,
∴分式方程+1=的解为x=1.
(2)解不等式2x>1﹣x,得:x>;
解不等式4x+2<x+4,得:x<.
∴不等式组的解集为<x<.
21.解:(1)∵44÷22%=200(名)
∴该调查的样本容量为200;
a=24÷200=12%,
b=72÷200=36%,
“常常”对应扇形的圆心角为:
360°×30%=108°.
(2)200×30%=60(名)
.
(3)∵3200×36%=1152(名)
∴“总是”对错题进行整理、分析、改正的学生有1152名.
故答案为:200、12、36、108.
22.解:画树状图为:
共有8种等可能的结果数,其中至少有两瓶为红枣口味的结果数为4,
所以该住户收到的三瓶酸奶中,至少有两瓶为红枣口味的概率==.
23.证明:(1)∵△ACD是等边三角形,
∴∠DCA=60°,
∵∠BAC=60°,
∴∠DCA=∠BAC,
在△ABE与△CFE中,
,
∴△ABE≌△CFE;
(2)∵E是AC的中点,
∴BE=EA,
∵∠BAE=60°,
∴△ABE是等边三角形,
∴△CEF是等边三角形,
∴∠CFE=60°,
∵△ACD是等边三角形,
∴∠CDA=∠DCA=60°,
∴∠CFE=∠CDA,
∴BF∥AD,
∵∠DCA=∠BAC=60°,
∴AB∥DC,
∴四边形ABFD是平行四边形.
24.解:(1)设小丽购买自动铅笔x支,记号笔y支,根据题意可得:
,
解得:,
答:小丽购买自动铅笔1支,记号笔2支;
(2)设小丽购买软皮笔记本m本,自动铅笔n支,根据题意可得:
m+1.5n=15,
∵m,n为正整数,
∴或或,
答:共3种方案:1本软皮笔记本与7支记号笔;
2本软皮笔记本与4支记号笔;3本软皮笔记本与1支记号笔.
25.解:(1)如图,作DE⊥AC于点E,
再Rt△CDE中,sinC=,
∴=,
∴DE=4,
答:点D到CA的距离为4;
(2)在Rt△CDE中,∠C=45°,
∴△CDE为等腰直角三角形,
∴CE=DE=4,
∵∠ADB=75°,∠C=45°,
∴∠EAD=∠ADB﹣∠C=30°,
∴在Rt△ADE中,tan∠EAD=,
∴=,
∴AE=4,
∴AC=AE+CE=4+4,
在Rt△ABC中,sinC=,
∴=,
∴AB=4+4,
答:旗杆AB的高为(4+4)m.
26.解:(1)设一次函数表达式为y=kx+b(k≠0),依题意得:
,解得:.
∴y与x之间的函数表达式为y=﹣x+190(180≤x≤300).
(2)设房价为x元(180≤x≤300)时,宾馆当日利润为w元,依题意得:
w=(﹣x+190)(x﹣100)﹣60×[100﹣(﹣x+190)]=﹣+210x﹣13600=﹣(x﹣210)2+8450,
∴当x=210时,w取最大值,最大值为8450.
答:当房价为210元时,宾馆当日利润最大,最大利润为8450元.
27.解:(1)∵CM=x,BC=6,
∴设HC=y,则BH=HM=6﹣y,
故y2+x2=(6﹣y)2,
整理得:y=﹣x2+3,
故答案为:﹣x2+3;
(2)∵四边形ABCD为正方形,
∴∠B=∠C=∠D=90°,
设CM=x,由题意可得:ED=3,DM=6﹣x,∠EMH=∠B=90°,
故∠HMC+∠EMD=90°,
∵∠HMC+∠MHC=90°,∴∠EMD=∠MHC,
∴△EDM∽△MCH,
∴=,
即=,
解得:x1=2,x2=6(不合题意舍去),
∴CM=2,
∴DM=4,
∴在Rt△DEM中,由勾股定理得:EM=5,
∴NE=MN﹣EM=6﹣5=1,
∵∠NEG=∠DEM,∠N=∠D,
∴△NEG∽△DEM,
∴=,
∴=,
解得:NG=,
由翻折变换的性质,得AG=NG=,
过点G作GP⊥BC,垂足为P,
则BP=AG=,GP=AB=6,
当x=2时,CH=﹣x2+3=,
∴PH=BC﹣HC﹣BP=6﹣﹣=2,
在Rt△GPH中,GH===2.
28.解:(1)由题意解得,
∴抛物线解析式为y=x2﹣x﹣,
∵y=x2﹣x﹣=(x﹣)2﹣,
∴顶点坐标(,﹣).
(2)如图1中,连接AB,作DH⊥AB于H,交OB于P,
此时PB+PD最小.
理由:∵OA=1,OB=,
∴tan∠ABO==,
∴∠ABO=30°,
∴PH=PB,
∴PB+OD=PH+PD=DH,
∴此时PB+PD最短(垂线段最短).
在RT△ADH中,∵∠AHD=90°,AD=,∠HAD=60°,
∴sin60°=,
∴DH=,
∴PB+PD的最小值为.
故答案为.
(3)①以A为圆心AB为半径画弧与对称轴有两个交点,
以B为圆心AB为半径画弧与对称轴也有两个交点,
线段AB的垂直平分线与对称轴有一个交点,
所以满足条件的点M有5个,即满足条件的点N也有5个,
故答案为5.
②如图,RT△AOB中,∵tan∠ABO==,
∴∠ABO=30°,
作AB的中垂线与y轴交于点E,连接EA,则∠AEB=120°,
以E为圆心,EB为半径作圆,与抛物线对称轴交于点F、G.
则∠AFB=∠AGB=60°,从而线段FG上的点满足题意,
∵EB==,
∴OE=OB﹣EB=,
∵F(,t),EF2=EB2,
∴()2+(t+)2=()2,
解得t=或,
故F(,),G(,),
∴t的取值范围≤t≤
2017年徐州市中考数学试卷
一、选择题(本大题共8小题,每小题3分,共24分)
1.﹣5的倒数是( )[来%源:@~中教^网#]
A.﹣5 B.5 C. D.
2.下列图形中,既是轴对称图形,又是中心对称图形的是( )
A. B. C. D.
3.肥皂泡的泡壁厚度大约是0.00000071米,数字0.00000071用科学记数法表示为( )
A.7.1×107 B.0.71×10﹣6 C.7.1×10﹣7 D.71×10﹣8
4.下列运算正确的是( )
A.a﹣(b+c)=a﹣b+c B.2a2•3a3=6a5 C.a3+a3=2a6 D.(x+1)2=x2+1
5.在“朗读者”节目的影响下,某中学开展了“好书伴我成长”读书活动,为了解5月份八年级300名学生读书情况,随机调查了八年级50名学生读书的册数,统计数据如下表所示:[来源:中国教^~育出版网%#@]
册数
0
1
2
3
4
人数
4
12
16
17
1
关于这组数据,下列说法正确的是( )
A.中位数是2 B.众数是17 C.平均数是2 D.方差是2
6.如图,点A,B,C在⊙O上,∠AOB=72°,则∠ACB等于( )
A.28° B.54° C.18° D.36°
7.如图,在平面直角坐标系xOy中,函数y=kx+b(k≠0)与y=(m≠0)的图象相交于点A(2,3),B(﹣6,﹣1),则不等式kx+b>的解集为( )
A.x<﹣6 B.﹣6<x<0或x>2 C.x>2 D.x<﹣6或0<x<2
8.若函数y=x2﹣2x+b的图象与坐标轴有三个交点,则b的取值范围是( )[
:A.b<1且b≠0 B.b>1 C.0<b<1 D.b<1[来#源*:@^%中教网]
二、填空题(本大题共10小题,每小题3分,共30分)
9.4的算术平方根是 .
10.如图,转盘中6个扇形的面积相等,任意转动转盘1次,当转盘停止转动时,指针指向的数小于5的概率为 .
11.使有意义的x的取值范围是 .
12.反比例函数y=的图象经过点M(﹣2,1),则k= .
13.△ABC中,点D,E分别是AB,AC的中点,DE=7,则BC= .[www.z#z%&step^@.com]
14.已知a+b=10,a﹣b=8,则a2﹣b2= .
15.正六边形的每个内角等于 .
16.如图,AB与⊙O相切于点B,线段OA与弦BC垂直,垂足为D,AB=BC=2,则∠AOB= .
17.如图,矩形ABCD中,AB=4,AD=3,点Q在对角线AC上,且AQ=AD,连接DQ并延长,与边BC交于点P,则线段AP= .
18.如图,已知OB=1,以OB为直角边作等腰直角三角形A1BO,再以OA1为直角边作等腰直角三角形A2A1O,如此下去,则线段OAn的长度为 .
三、解答题(本大题共10小题,共86分)
19.计算:(1)(﹣2)2﹣()﹣1+20170 ] (2)(1+)÷.
20.(1)解方程: =[来源:中#国&*教育出@版~ (2)解不等式组:.
21.某校园文学社为了解本校学生对本社一种报纸四个版面的喜欢情况,随机抽查部分学生做了一次问卷调查,要求学生选出自己最喜欢的一个版面,将调查数据进行了整理、绘制成部分统计图如下:
请根据图中信息,解答下列问题:[中@国教育%出版&#网*]
(1)该调查的样本容量为 ,a= %,“第一版”对应扇形的圆心角为 °;[中国*^教~育#&出版网]
(2)请你补全条形统计图;
(3)若该校有1000名学生,请你估计全校学生中最喜欢“第三版”的人数.
22.一个不透明的口袋中装有4张卡片,卡片上分别标有数字1,﹣3,﹣5,7,这些卡片数字外都相同,小芳从口袋中随机抽取一张卡片,小明再从剩余的三张卡片中随机抽取一张,请你用画树状图或列表的方法,求两人抽到的数字符号相同的概率.
23.如图,在▱ABCD中,点O是边BC的中点,连接DO并延长,交AB延长线于点E,连接BD,EC.
(1)求证:四边形BECD是平行四边形;
(2)若∠A=50°,则当∠BOD= °时,四边形BECD是矩形.[来%源:@~z&zste#p.com]
24.4月9日上午8时,2017徐州国际马拉松赛鸣枪开跑,一名34岁的男子带着他的两个孩子一同参加了比赛,下面是两个孩子与记者的对话:
根据对话内容,请你用方程的知识帮记者求出哥哥和妹妹的年龄.
25.如图,已知AC⊥BC,垂足为C,AC=4,BC=3,将线段AC绕点A按逆时针方向旋转60°,得到线段AD,连接DC,DB.
(1)线段DC= ;
(2)求线段DB的长度.
26.如图①,菱形ABCD中,AB=5cm,动点P从点B出发,沿折线BC﹣CD﹣DA运动到点A停止,动点Q从点A出发,沿线段AB运动到点B停止,它们运动的速度相同,设点P出发xs时,△BPQ的面积为ycm2,已知y与x之间的函数关系如图②所示,其中OM,MN为线段,曲线NK为抛物线的一部分,请根据图中的信息,解答下列问题:
(1)当1<x<2时,△BPQ的面积 (填“变”或“不变”);
(2)分别求出线段OM,曲线NK所对应的函数表达式;
(3)当x为何值时,△BPQ的面积是5cm2?
27.如图,将边长为6的正三角形纸片ABC按如下顺序进行两次折叠,展平后,得折痕AD,BE(如图①),点O为其交点.
(1)探求AO到OD的数量关系,并说明理由;
(2)如图②,若P,N分别为BE,BC上的动点.
①当PN+PD的长度取得最小值时,求BP的长度;
②如图③,若点Q在线段BO上,BQ=1,则QN+NP+PD的最小值= .
[w*ww.~z@zs%tep.co#m]
28.如图,已知二次函数y=x2﹣4的图象与x轴交于A,B两点,与y轴交于点C,⊙C的半径为,P为⊙C上一动点.
(1)点B,C的坐标分别为B ,C ;
(2)是否存在点P,使得△PBC为直角三角形?若存在,求出点P的坐标;若不存在,请说明理由;
(3)连接PB,若E为PB的中点,连接OE,则OE的最大值= .
2017年徐州市中考数学试卷答案
1. D.[中国教^&%育*出版网@] 2. C.3. C. 4. B.5. A.6. D.7. B.8. A.
9. 2. 10. .11. x≥6.[来@源:中#国教育^出*版网&] 12.﹣2. 13. 14. 14. 80[中%@国#教^育*出版网] 15. 120° 16. 60. 17. .18.
19.解:(1)(﹣2)2﹣()﹣1+20170=4﹣2+1=3;
(2)(1+)÷===x﹣2.
20.解:(1)=,
去分母得:2(x+1)=3x,解得:x=2,
经检验x=2是分式方程的解,故原方程的解为x=2;[ww&w.#z~zstep^.com*]
(2),[www@.zzstep.c~^*#om]
由①得:x>0;
由②得:x<5,
故不等式组的解集为0<x<5.
21.解:(1)设样本容量为x.
由题意=10%,解得x=50,a=×100%=36%,
第一版”对应扇形的圆心角为360°×=108°故答案分别为50,36,108.
(2)“第三版”的人数为50﹣15﹣5﹣18=12,
条形图如图所示,[来源@:zzst*ep.c~om%^]
(3)该校有1000名学生,估计全校学生中最喜欢“第三版”的人数约为1000××100%=240人.
22.解:画树状图为:[中~国%教@*育出版网&]
共有12种等可能的结果数,其中两人抽到的数字符号相同的结果数为4,
所以两人抽到的数字符号相同的概率==.[来~%#源:中国教育出*版&网]
23.(1)证明:∵四边形ABCD为平行四边形,
∴AB∥DC,AB=CD,
∴∠OEB=∠ODC,
又∵O为BC的中点,
∴BO=CO,
在△BOE和△COD中,,[中@~国教育出#&版*网]
∴△BOE≌△COD(AAS);
∴OE=OD,
∴四边形BECD是平行四边形;
(2)解:若∠A=50°,则当∠BOD=100°时,四边形BECD是矩形.理由如下:
∵四边形ABCD是平行四边形,
∴∠BCD=∠A=50°,
∵∠BOD=∠BCD+∠ODC,
∴∠ODC=100°﹣50°=50°=∠BCD,
∴OC=OD,[来@源*:中教&%网^]
∵BO=CO,OD=OE,∴DE=BC,
∵四边形BECD是平行四边形,
∴四边形BECD是矩形;故答案为:100.
24.解:设今年妹妹的年龄为x岁,哥哥的年龄为y岁,
根据题意得:,
解得:.
答:今年妹妹6岁,哥哥10岁.[中国^教@&育出版%网*]
25.解:(1)∵AC=AD,∠CAD=60°,
∴△ACD是等边三角形,[来&源:中国^%教@育出版~网]∴DC=AC=4.故答案是:4;[来&#源%:中国^教~育出版网]
(2)作DE⊥BC于点E.
∵△ACD是等边三角形,∴∠ACD=60°,
又∵AC⊥BC,
∴∠DCE=∠ACB﹣∠ACD=90°﹣60°=30°,[中&国教育出版@*#%网]
∴Rt△CDE中,DE=DC=2,
CE=DC•cos30°=4×=2,[来源:zzs@te%p.~co&*m]
∴BE=BC﹣CE=3﹣2=.
∴Rt△BDE中,BD===.[来源:中*国教育出^版网@&#]
26.解:(1)由函数图象知,当1<x<2时,△BPQ的面积始终等于10,
∴当1<x<2时,△BPQ的面积不变;
故答案为:不变;
(2)设线段OM的函数表达式为y=kx,
把(1,10)代入得,k=10,[来源&:中^*教@#网]
∴线段OM的函数表达式为y=10x;
设曲线NK所对应的函数表达式y=a(x﹣3)2,
把(2,10)代入得,10=a(2﹣3)2,
∴a=10,
∴曲线NK所对应的函数表达式y=10(x﹣3)2;
(3)把y=5代入y=10x得,x=,
把y=5代入y=10(x﹣3)2得,5=10(x﹣3)2,
∴x=3±,
∵3+>3,[来&^源#:中国~教育出版网@]
∴x=3﹣,
∴当x=或3﹣时,△BPQ的面积是5cm2.
27.解:(1)AO=2OD,
理由:∵△ABC是等边三角形,
∴∠BAO=∠ABO=∠OBD=30°,
∴AO=OB,
∵BD=CD,
∴AD⊥BC,
∴∠BDO=90°,
∴OB=2OD,
∴OA=2OD;
(2)如图②,作点D关于BE的对称点D′,过D′作D′N⊥BC于N交BE于P,
则此时PN+PD的长度取得最小值,
∵BE垂直平分DD′,
∴BD=BD′,
∵∠ABC=60°,
∴△BDD′是等边三角形,
∴BN=BD=,
∵∠PBN=30°,
∴=,
∴PB=;
(3)如图③,作Q关于BC的对称点Q′,作D关于BE的对称点D′,
连接Q′D′,即为QN+NP+PD的最小值.
根据轴对称的定义可知:∠Q′BN=∠QBN=30°,∠QBQ′=60°,
∴△BQQ′为等边三角形,△BDD′为等边三角形,[中国教&育%出@版网*#]
∴∠D′BQ′=90°,
∴在Rt△D′BQ′中,
D′Q′==.[中~^#国教育出版网&%]
∴QN+NP+PD的最小值=,
故答案为:.
28.解:(1)在y=x2﹣4中,令y=0,则x=±3,令x=0,则y=﹣4,
∴B(3,0),C(0,﹣4);
故答案为:3,0;0,﹣4;
(2)存在点P,使得△PBC为直角三角形,
①当PB与⊙相切时,△PBC为直角三角形,如图(2)a,
连接BC,
∵OB=3.OC=4,
∴BC=5,
∵CP2⊥BP2,CP2=,
∴BP2=2,
过P2作P2E⊥x轴于E,P2F⊥y轴于F,
则△CP2F∽△BP2E,四边形OCP2B是矩形,
∴==2,
设OC=P2E=2x,CP2=OE=x,
∴BE=3﹣x,CF=2x﹣4,
∴==2,[来源~&:中@^教%网]
∴x=,2x=,
∴FP2=,EP2=,
∴P2(,﹣),
过P1作P1G⊥x轴于G,P1H⊥y轴于H,
同理求得P1(﹣1,﹣2),
②当BC⊥PC时,△PBC为直角三角形,
过P4作P4H⊥y轴于H,
则△BOC∽△CHP4,
∴==,
∴CH=,P4H=,
∴P4(,﹣﹣4);[来源@~:中^国教育出&版网#]
同理P3(﹣,﹣4);
综上所述:点P的坐标为:(﹣1,﹣2)或(,﹣)或(,﹣﹣4)或(﹣,﹣4);
(3)如图(3),当PB与⊙C相切时,PB与y 轴的距离最大,OE的值最大,[www.z@zs^te%p~.com#]
∵过E作EM⊥y轴于M,过P作PF⊥y轴于F,
∴OB∥EM∥PF,
∵E为PB的中点,
∴ME=(OB+PF)=,OM=MF=OF=,
∴OE==.
故答案为:.
[来源:%中*#国教~育出@版网]
2018年徐州市中考数学试卷
一、选择题(共8小题,每小题3分,满分24分)
1.4的相反数是( )
A. B.﹣ C.4 D.﹣4
2.下列计算正确的是( )
A.2a2﹣a2=1 B.(ab)2=ab2 C.a2+a3=a5 D.(a2)3=a6
3.下列图形中,既是轴对称图形,又是中心对称图形的是( )
A. B. C. D.
4.如图是由5个相同的正方体搭成的几何体,其左视图是( )
A. B. C. D.
5.抛掷一枚质地均匀的硬币,若前3次都是正面朝上,则第4次正面朝上的概率( )
A.小于 B.等于 C.大于 D.无法确定
6.某市从不同学校随机抽取100名初中生,对“学校统一使用数学教辅用书的册数”进行调查,统计结果如下:结果如下:
册数
0
1
2
3
人数
13
35
29
23
关于这组数据,下列说法正确的是( )
A.众数是2册 B.中位数是2册 C.极差是2册 D.平均数是2册
7.如图,在平面直角坐标系中,函数y=kx与y=﹣的图象交于A,B两点,过A作y轴的垂线,交函数y=的图象于点C,连接BC,则△ABC的面积为( )
A.2 B.4 C.6 D.8
8.若函数y=kx+b的图象如图所示,则关于x的不等式kx+2b<0的解集为( )
A.x<3 B.x>3 C.x<6 D.x>6
第7题图 第8题图 第15题图 第16题图
二、填空题(本大题共有10小题,每小题3分,共30分)
9.五边形的内角和是 °.
10.我国自主研发的某型号手机处理器采用10nm工艺,已知1nm=0.000000001m,则10nm用科学记数法可表示为 m.
11.化简:||= .
12.若在实数范围内有意义,则x的取值范围为 .
13.若2m+n=4,则代数式6﹣2m﹣n的值为 .
14.若菱形两条对角线的长分别是6cm和8cm,则其面积为 cm2.
15.如图,Rt△ABC中,∠ABC=90°,D为AC的中点,若∠C=55°,则∠ABD= °.
16.如图,扇形的半径为6,圆心角θ为120°,用这个扇形围成一个圆锥的侧面,所得圆锥的底面半径为 .
17.如图,每个图案均由边长相等的黑、白两色正方形按规律拼接而成,照此规律,第n个图案中白色正方形比黑色正方形多 个.(用含n的代数式表示)
18.如图,AB为⊙O的直径,AB=4,C为半圆AB的中点,P为上一动点,延长BP至点Q,使BP•BQ=AB2.若点P由A运动到C,则点Q运动的路径长为 .
三、解答题(本大题共有10小题,共86分)
19.(10分)计算:
(1)﹣12+20180﹣()﹣1+; (2)÷.
20.(10分)(1)解方程:2x2﹣x﹣1=0; (2)解不等式组:
21.(7分)不透明的袋中装有1个红球与2个白球,这些球除颜色外都相同,将其搅匀.
(1)从中摸出1个球,恰为红球的概率等于 ;
(2)从中同时摸出2个球,摸到红球的概率是多少?(用画树状图或列表的方法写出分析过程)
22.(7分)在“书香校园”活动中,某校为了解学生家庭藏书情况,随机抽取本校部分学生进行调查,并绘制成部分统计图表如下:
类别
家庭藏书m本
学生人数
A
0≤m≤25
20
B
26≤m≤100
a
C
101≤m≤200
50
D
m≥201
66
根据以上信息,解答下列问题:
(1)该调查的样本容量为 ,a= ;
(2)在扇形统计图中,“A”对应扇形的圆心角为 °;
(3)若该校有2000名学生,请估计全校学生中家庭藏书200本以上的人数.
23.(8分)如图,在矩形ABCD中,AD=4,点E在边AD上,连接CE,以CE为边向右上方作正方形CEFG,作FH⊥AD,垂足为H,连接AF.
(1)求证:FH=ED;(2)当AE为何值时,△AEF的面积最大?
24.(8分)徐州至北京的高铁里程约为700km,甲、乙两人从徐州出发,分别乘坐“徐州号”高铁A与“复兴号”高铁B前往北京.已知A车的平均速度比B车的平均速度慢80km/h,A车的行驶时间比B车的行驶时间多40%,两车的行驶时间分别为多少?
25.(8分)如图,AB为⊙O的直径,点C在⊙O外,∠ABC的平分线与⊙O交于点D,∠C=90°.
(1)CD与⊙O有怎样的位置关系?请说明理由;(2)若∠CDB=60°,AB=6,求的长.
26.(8分)如图,1号楼在2号楼的南侧,两楼高度均为90m,楼间距为AB.冬至日正午,太阳光线与水平面所成的角为32.3°,1号楼在2号楼墙面上的影高为CA;春分日正午,太阳光线与水平面所成的角为55.7°,1号楼在2号楼墙面上的影高为DA.已知CD=42m.
(1)求楼间距AB;
(2)若2号楼共30层,层高均为3m,则点C位于第几层?(参考数据:sin32.3°≈0.53,cos32.3°≈0.85,tan32.3°≈0.63,sin55.7°≈0.83,cos55.7°≈0.56,tan55.7°≈1.47)
27.(10分)如图,在平面直角坐标系中,二次函数y=﹣x2+6x﹣5的图象与x轴交于A、B两点,与y轴交于点C,其顶点为P,连接PA、AC、CP,过点C作y轴的垂线l.
(1)求点P,C的坐标;
(2)直线l上是否存在点Q,使△PBQ的面积等于△PAC的面积的2倍?若存在,求出点Q的坐标;若不存在,请说明理由.
28.(10分)如图,将等腰直角三角形纸片ABC对折,折痕为CD.展平后,再将点B折叠在边AC上(不与A、C重合),折痕为EF,点B在AC上的对应点为M,设CD与EM交于点P,连接PF.已知BC=4.
(1)若M为AC的中点,求CF的长;
(2)随着点M在边AC上取不同的位置,
①△PFM的形状是否发生变化?请说明理由;
②求△PFM的周长的取值范围.
2018年徐州市中考数学试卷答案
1. D.2. D.3. A.4. A.5. B.6. B.7. C.8. D.
9. 540°. 10. 1×10﹣8.11. 2﹣. 12.x≥2.13. 2.14. 24.15. 35.16. 2.17. 4n+3个.18. 4.
19.解:(1)﹣12+20180﹣()﹣1+;
=﹣1+1﹣2+2,
=0;
(2)÷.
=÷,
=2a﹣2b.
20.解:(1)2x2﹣x﹣1=0,
(2x+1)(x﹣1)=0,
2x+1=0,x﹣1=0,
x1=﹣,x2=1
(2)
∵解不等式①得:x>﹣4,
解不等式②得:x≤3,
∴不等式组的解集为﹣4<x≤3.
21.解:(1)从中摸出1个球,恰为红球的概率等于,
故答案为:;
(2)画树状图:
所以共有6种情况,含红球的有4种情况,
所以p==,
答:从中同时摸出2个球,摸到红球的概率是.
22.解:(1)因为“C”有50人,占样本的25%,
所以样本=50÷25%=200(人)
因为“B”占样本的32%,
所以a=200×32%=64(人)
故答案为:200,64;
(2)“A”对应的扇形的圆心角=×360°=36°,
故答案为:36°;
(3)全校学生中家庭藏书200本以上的人数为:
2000×=660(人)
答:全校学生中家庭藏书200本以上的人数为660人.
23.解:(1)证明:
∵四边形CEFG是正方形,
∴CE=EF,
∵∠FEC=∠FEH+∠CED=90°,∠DCE+∠CED=90°,
∴∠FEH=∠DCE,
在△FEH和△ECD中
,
∴△FEH≌△ECD,
∴FH=ED;
(2)设AE=a,则ED=FH=4﹣a,
∴S△AEF=AE•FH=a(4﹣a),
=﹣(a﹣2)2+2,
∴当AE=2时,△AEF的面积最大.
24.解:设B车行驶的时间为t小时,则A车行驶的时间为1.4t小时,
根据题意得:﹣=80,
解得:t=2.5,
经检验,t=2.5是原分式方程的解,且符合题意,
∴1.4t=2.5.
答:A车行驶的时间为2.5小时,B车行驶的时间为2.5小时.
25.解:(1)相切.理由如下:
连接OD,
∵BD是∠ABC的平分线,
∴∠CBD=∠ABD,
又∵OD=OB,
∴∠ODB=∠ABD,
∴∠ODB=∠CBD,
∴OD∥CB,
∴∠ODC=∠C=90°,
∴CD与⊙O相切;
(2)若∠CDB=60°,可得∠ODB=30°,
∴∠AOD=60°,
又∵AB=6,
∴AO=3,
∴==π.
26.解:(1)过点C作CE⊥PB,垂足为E,过点D作DF⊥PB,垂足为F,
则∠CEP=∠PFD=90°,
由题意可知:设AB=x,在Rt△PCE中,
tan32.3°=,
∴PE=x•tan32.3°,
同理可得:在Rt△PDF中,
tan55.7°=,
∴PF=x•tan55.7°,
由PF﹣PE=EF=CD=42,
可得x•tan55.7°﹣x•tan32.3°=42,
解得:x=50
∴楼间距AB=50m,
(2)由(1)可得:PE=50•tan32.3°=31.5m,
∴CA=EB=90﹣31.5=58.5m
由于2号楼每层3米,可知点C位于20层
27.解:(1)∵y=﹣x2+6x﹣5=﹣(x﹣3)2+4,
∴顶点P(3,4),
令x=0得到y=﹣5,
∴C(0.﹣5).
(2)令y=0,x2﹣6x+5=0,解得x=1或5,
∴A(1,0),B(5,0),
设直线PC的解析式为y=kx+b,则有,
解得,
∴直线PC的解析式为y=3x﹣5,设直线交x轴于D,则D(,0),
设直线PQ交x轴于E,当BE=2AD时,△PBQ的面积等于△PAC的面积的2倍,
∵AD=,
∴BE=,
∴E(,0)或E′(,0),
则直线PE的解析式为y=﹣6x+22,
∴Q(,﹣5),
直线PE′的解析式为y=﹣x+,
∴Q′(,﹣5),
综上所述,满足条件的点Q(,﹣5),Q′(,﹣5).
28.解:(1)∵M为AC的中点,
∴CM=AC=BC=2,
由折叠的性质可知,FB=FM,
设CF=x,则FB=FM=4﹣x,
在Rt△CFM中,FM2=CF2+CM2,即(4﹣x)2=x2+22,
解得,x=,即CF=;
(2)①△PFM的形状是等腰直角三角形,不会发生变化,
理由如下:由折叠的性质可知,∠PMF=∠B=45°,
∵CD是中垂线,
∴∠ACD=∠DCF=45°,
∵∠MPC=∠OPM,
∴△POM∽△PMC,
∴=,
∴=
∵∠EMC=∠AEM+∠A=∠CMF+∠EMF,
∴∠AEM=∠CMF,
∵∠DPE+∠AEM=90°,∠CMF+∠MFC=90°,∠DPE=∠MPC,
∴∠DPE=∠MFC,∠MPC=∠MFC,
∵∠PCM=∠OCF=45°,
∴△MPC∽△OFC,
∴=,
∴=,
∴=,∵∠POF=∠MOC,
∴△POF∽△MOC,
∴∠PFO=∠MCO=45°,
∴△PFM是等腰直角三角形.
②∵△PFM是等腰直角三角形,设FM=y,
由勾股定理可知:PF=PM=y,
∴△PFM的周长=(1+)y,
∵2<y<4,
∴△PFM的周长满足:2+2<(1+)y<4+4.
2023年江苏省徐州市中考数学试卷: 这是一份2023年江苏省徐州市中考数学试卷,共32页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
2023年江苏省徐州市中考数学试卷: 这是一份2023年江苏省徐州市中考数学试卷,共32页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
2021年江苏省徐州市中考数学试卷: 这是一份2021年江苏省徐州市中考数学试卷,共29页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。












