吉林省松原市前郭尔罗斯蒙古族自治县2022-2023学年七年级下学期期末考试数学试卷(含解析)

;

前郭县2022—2023学年度第二学期期末考试

七年级数学试卷

一、单项选择题（每小题2分，共12分）

1．实数，0.3，，，，0.1010010001…（依次增加一个0）中，无理数的个数是（    ）

A．2 B．3 C．4 D．5

2．下列说法正确的是（   ）

A．过直线外一点作已知直线的垂线段，就是点到直线的距离

B．垂线段最短

C．过一点有且只有一条直线与已知直线平行

D．同一平面内，两条直线的位置关系为平行和垂直

3．下列方程组中是二元一次方程组的是（    ）

A． B． C． D．

4．已知，下列结论正确的是（       ）

A． B． C． D．

5．若点在第二象限，点到轴的距离是7，到轴的距离是3，点的坐标是（    ）

A． B． C． D．

6．为了解某市参加中考的51000名学生的视力情况，抽查了其中1500名学生的视力情况进行统计分析，下列叙述正确的是（    ）

A．51000名学生是总体

B．每名学生是总体的一个个体

C．1500名学生的视力情况是总体的一个样本

D．以上调查是普查

二、填空题(每小题3分，共24分)

7．某节能灯生产厂家为了解一批产品（灯泡）的使用寿命，应该采用的调查方是     ．（选填“全面调查”或“抽样调查”）．

8．的平方根是        

9．若是二元一次方程，则           ，           ．

10．不等式3x﹣2≥4（x﹣1）的所有非负整数解的和为  ．

11．如图，有一块含有45°角的直角三角板两个顶点放在直尺对边上，如果∠1=20°，那么∠2的度数是     ．

12．如图，将直角三角形沿方向平移得到直角三角形．已知，则长为     ．

13．如图，在平面直角坐标系中，已知点，，，，一智能机器人从点出发，以每秒1个单位长度的速度沿方向匀速循环前行，当机器人前行了2023秒时，其所在位置的点的坐标为      ．

14．我国古典数学文献《增删算法统宗正六均输》中有一个“隔沟计算”的问题：“甲乙隔沟牧放，二人暗里参详，甲云得乙九只羊，多乙一倍之上，乙说得甲九只，两家之数相当，二人闲坐恼心肠，画地算了半晌”，其大意为：甲、乙两人一起放牧，两人心里暗中数羊．如果乙给甲9只羊，那么甲的羊数为乙的2倍；如果甲给乙9只羊，那么两人的羊数相同，请问甲，乙各有多少只羊？设甲有羊x只，乙有羊y只，根据题意，可列方程组为        ．

三、解答题（每题5分，共20分）

15．计算：

16．已知的算术平方根是3，的立方根是2，求的平方根．

17．解不等式组：并在数轴上把解集表示出来．

18．已知：如图，直线与相交于点，是的平分线，如果．求的度数．

四、解答题（每小题7分，共28分） 

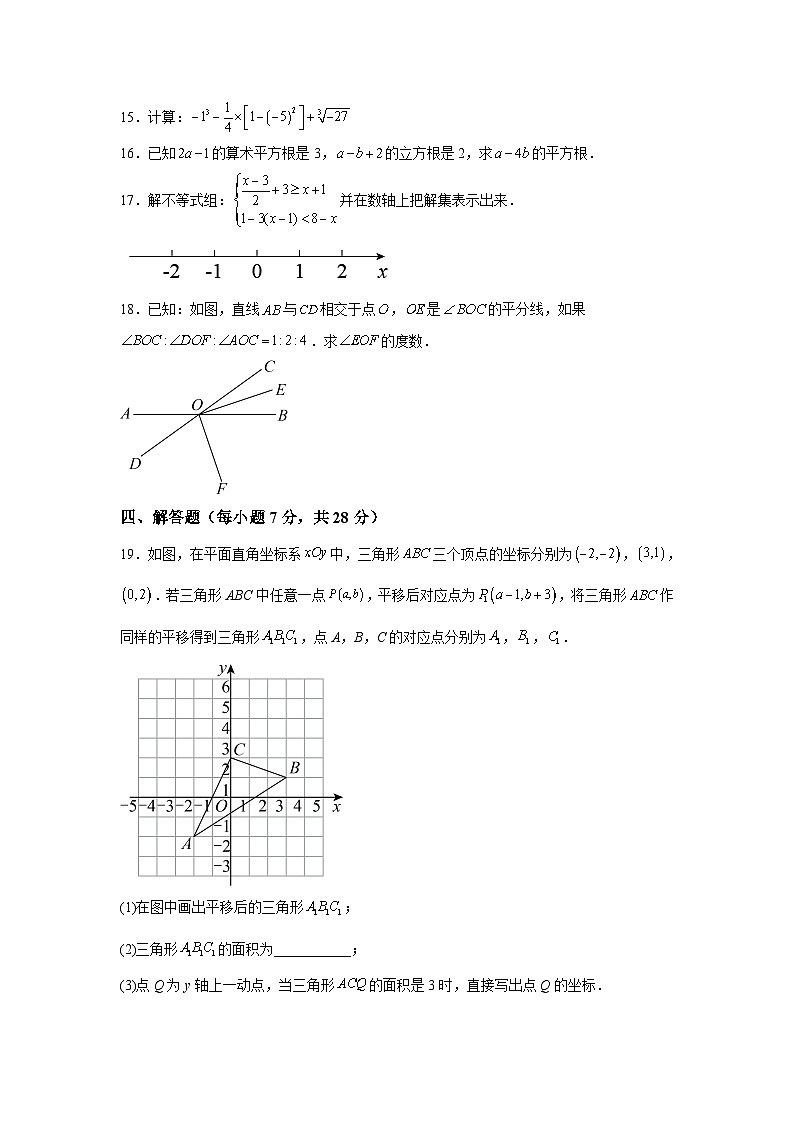
19．如图，在平面直角坐标系中，三角形三个顶点的坐标分别为，，．若三角形ABC中任意一点，平移后对应点为，将三角形作同样的平移得到三角形，点A，B，C的对应点分别为，，．

(1)在图中画出平移后的三角形；

(2)三角形的面积为___________；

(3)点Q为y轴上一动点，当三角形的面积是3时，直接写出点Q的坐标．

20．已知关于，的二元一次方程组的解满足，求满足条件的的所有非负整数值．

21．如图，已知，，．试说明直线与的位置关系．

22．甲、乙两人解同一个方程组  , 甲因看错①中的得解为，乙因抄错了②中的解得，请求出原方程组的解．

五、解答题（每小题8分，共16分） 

23．某校想了解学生每周的课外阅读时间情况，随机调查了部分学生，对学生每周的课外阅读时间 x 小时进行分组整理，并绘制了不完整的频数分布直方图和扇形统计图(如图) ，根据图中提供的信息，解答下列问题：

(1) 这次抽样调查的学生人数是　　　人；

(2) 扇形统计图中 “A”组对应的圆心角度数为　　　，并将直方图补充完整；

(3) 若该校有 2000 名学生，试估计全校有多少名学生每周的课外阅读时间不少于 6 小时？

24．在平面直角坐标系中，对于点，若点Q的坐标为，其中a为常数，则称点Q是点P的“a级关联点”．

(1)已知点的“级关联点”是点，则点的坐标为______；

(2)已知点的“级关联点”N位于x轴上，求点N的坐标；

(3)在（2）的条件下，若存在点H，使轴，且，直接写出H点坐标．

六、解答题（每小题10分，共20分）

25．A、B两超市平日都是以同样的价格出售同样的商品，如笔记本每本18元，练习本每本3元．

（1）若小丽一日在A超市购买了笔记本和练习本共7本，总共花费了51元，则小丽笔记本和练习本各买了多少本？

（2）某节假日，A、B两超市推出不同的优惠方案：在A超市累计购物超过50元的部分打九折；在B超市累计购物超过80元的部分打八点五折．

①若小丽购物金额超过80元，则她去哪家超市购物更合算？

②若小丽打算到A超市购买一些笔记本送给同学，请问她至少购买多少本时，平均每本笔记本价格不超过17元？

26．如图，PQ∥MN，A、B分别为直线MN、PQ上两点，且∠BAN＝45°，若射线AM绕点A顺时针旋转至AN后立即回转，射线BQ绕点B逆时针旋转至BP后立即回转，两射线分别绕点A、点B不停地旋转，若射线AM转动的速度是a°/秒，射线BQ转动的速度是b°/秒，且a、b满足|a﹣5|+（b﹣1）2＝0．（友情提醒：钟表指针走动的方向为顺时针方向）

（1）a＝　 　，b＝　 　；

（2）若射线AM、射线BQ同时旋转，问至少旋转多少秒时，射线AM、射线BQ互相垂直．

（3）若射线AM绕点A顺时针先转动18秒，射线BQ才开始绕点B逆时针旋转，在射线BQ到达BA之前，问射线AM再转动多少秒时，射线AM、射线BQ互相平行？

答案

1．B

解析：解：无理数有：，，0.1010010001…（依次增加一个0），共3个．

故选：B

2．B

解析：解：过直线外一点作已知直线的垂线段的长度，就是点到直线的距离，

故A说法错误，不符合题意；

垂线段最短，

故B说法正确，符合题意；

过直线外一点有且只有一条直线与已知直线平行，

故C说法错误，不符合题意；

同一平面内，两条直线的位置关系为平行和相交，

故D说法错误，不符合题意；

故选：B．

3．B

解析：A、不是整式方程，故此选项错误；

B、符合二元一次方程组的定义，故此选项正确；

C、含有三个未知数，故此选项错误；

D、未知数的次数是2，故此选项错误；

故选：B．

4．D

解析：A.，，原不等式不成立，此选项不符合题意；

B.当即时，原不等式不成立，此选项不符合题意；

C.当，时，原不等式不成立，此选项不符合题意；

D.，，，原不等式成立，此选项符合题意；

故选D．

5．C

解析：∵点在第二象限，

∴，，

∵点到轴的距离是7，

∴，

∴，

∵点到轴的距离是3，

∴，

∴，

∴点的坐标是．

故选C．

6．C

解析：A、51000名学生的视力情况是总体，选项错误；

B、每名学生的视力情况是总体的一个个体，选项错误；

C、1500名学生的视力情况是总体的一个样本，选项正确；

Ｄ、该调查属于抽样调查，选项错误．

故选：C

7．抽样调查

解析：某节能灯生产厂家为了解一批产品（灯泡）的使用寿命，应该采用的调查方是抽样调查

故答案为：抽样调查．

8．

解析：因为，6的平方根是±，所以的平方根是±.

故正确答案为±.

9．     4     2

解析：解：∵是二元一次方程，

∴ m－3＝1，n－1＝1，

解得 m＝4，n＝2，

故答案为：4，2

10．3.

解析：试题解析：

3x﹣2≥4（x﹣1），

3x﹣2≥4x﹣4，

x≤2，

所以不等式的非负整数解为0，1，2，

0+1+2=3，

11．25°

解析：解：如图：

∵，∠1=20°，

∴∠1=∠3=20°，

∴∠2=45°－20°=25°．

故答案为：25°．

12．

解析：解：∵平移前后对应点所连接的线段平行且相等，

∴，

∴，

故答案为：．

13．

解析：由点，，，，可知是长方形，

∴，，

∴机器人从点出发沿所走路程是：．

∵，

∴第2023秒时机器人在与轴的交点处，

∴机器人所在点的坐标为．

故答案为：

14．

解析：解：设甲有羊x只，乙有羊y只．

∵“如果乙给甲9只羊，那么甲的羊数为乙的2倍”，

∴；

∵“如果甲给乙9只羊，那么两人的羊数相同”，

∴．

联立两方程组成方程组．

故答案为：．

15．

解析：解：

．

16．

解析：解∵，

∴，

∵，

∴，

∴的平方根为：．

17．−2<x≤1，数轴见解析

解析：解：

解不等式①，得：x≤1，

解不等式②，得：x>−2，

∴不等式组的解集为−2<x≤1，

18．

解析：解：设，则，，

由题意得：，

解得：，

，，，

是的平分线，

．

∴

．

19．(1)见详解

(2)7

(3)或

解析：（1）解：∵三角形ABC中任意一点，经平移后对应点

∴三角形向左平移1单位、向上平移3单位

∴据此平移方式作图如下：

即为所求；

（2）解：的面积；

（3）解：设点Q的坐标为，则，

∴三角形的面积为，

解得：或5，

∴点Q坐标为或．

20．满足条件的的所有非负整数值为：0，1，2．

解析：解：，

①＋②得：，

∴.

把代入②得，

∴，

∴.

∵，

∴，

∴，

所以满足条件的的所有非负整数值为：0，1，2．

21．，理由见详解

解析：解：∵ （已知）

∴，（同位角相等，两直线平行）

∴（两直线平行，内错角相等）

又∵ （已知）

∴ （等量代换）

∴，（同旁内角互补，两直线平行）

∴ （两直线平行，同位角相等）

∵ （已知）

∴，（垂直的定义）

∴，（等量代换）

∴．（垂直的定义）

22．．

解析：解：，

把代入②得：，

解得：，

把代入①，得，

解得：，

即方程组为，

①②，得，

解得：，

把代入①，得，

解得：，

所以原方程组的解是．

23．(1)50;(2) 57.6 º; (3) 6小时.

解析：解：（1）这次调查的学生人数为8÷16%=50人，

故答案为：50；

（2）扇形统计图中“A”组对应的圆心角度数为360°×16%=57.6°，

B时间段的人数为50×30%=15人，

则D时间段的人数为50-（8+15+20+2）=5人，

补全图形如下：

故答案为：57.6°；

（3）（人）.

答：全校有280人每周的课外阅读时间不少于6小时.

24．(1)

(2)

(3)或

解析：（1）∵点的“级关联点”是点，

∴点坐标为，即，

故答案是；

（2）∵点的“级关联点” 是点N，

∴点坐标为，即，

∵点N位于x轴上，

∴，

∴，

∴，

∴；

（3）∵在（2）的条件下，，

∴，

∵轴，且，

∴或．

25．（1）小丽笔记本买了2本，练习本买了5本；（2）①当购物金额超过80元且不足140元时，小丽去A超市购物更划算；当购物金额为140元时，小丽去两家超市购物一样；当金额超过140元时，小丽去B超市购物更合算；②小丽至少购买7本时，平均每本笔记本价格不超过17元．

解析：解：（1）设小丽笔记本买了x本，练习本买了y本，根据题意可得：

，

解得：，

答：小丽笔记本买了2本，练习本买了5本．

（2）设小丽的购物原价为m（m＞80）元，由题意得：

在A超市购买需付金额为（元），

在B超市购买需付金额为（元），

当时，则有，

当时，则有，

当时，则有，

∴当购物金额超过80元且不足140元时，小丽去A超市购物更划算；当购物金额为140元时，小丽去两家超市购物一样；当金额超过140元时，小丽去B超市购物更合算；

（3）设小丽购买了n本笔记本，则总金额为（0.9×18n+5）元，由题意得：

，

解得：，

∵n为正整数，

∴n的最小值为7；

答：小丽至少购买7本时，平均每本笔记本价格不超过17元．

26．（1）a＝5，b＝1；（2）t＝15（s）；（3）15，22.5.

解析：解：（1）|a﹣5|+（b﹣1）2＝0，

∴a﹣5＝0，b﹣1＝0，

∴a＝5，b＝1，

故答案为5，1；

（2）设至少旋转t秒时，射线AM、射线BQ互相垂直．

如图，设旋转后的射线AM、射线BQ交于点O，则BO⊥AO，

∴∠ABO+∠BAO＝90°，

∵PQ∥MN，

∴∠ABQ+∠BAM＝180°，

∴∠OBQ+∠OAM＝90°，

又∵∠OBQ＝t°，∠OAM＝5t°，

∴t°+5t°＝90°，

∴t＝15（s）；

（3）设射线AM再转动t秒时，射线AM、射线BQ互相平行．

如图，射线AM绕点A顺时针先转动18秒后，AM转动至AM'的位置，∠MAM'＝18×5＝90°，

分两种情况：

①当9＜t＜18时，∠QBQ'＝t°，∠M'AM“＝5t°，

∵∠BAN＝45°＝∠ABQ，

∴∠ABQ'＝45°﹣t°，∠BAM“＝5t﹣45°，

当∠ABQ'＝∠BAM“时，BQ'∥AM“，

此时，45°﹣t°＝5t﹣45°，

解得t＝15；

②当18＜t＜27时，∠QBQ'＝t°，∠NAM“＝5t°﹣90°，

∵∠BAN＝45°＝∠ABQ，

∴∠ABQ'＝45°﹣t°，∠BAM“＝45°﹣（5t°﹣90°）＝135°﹣5t°，

当∠ABQ'＝∠BAM“时，BQ'∥AM“，

此时，45°﹣t°＝135°﹣5t，

解得t＝22.5；