





还剩27页未读,
继续阅读
中职数学基础模块上册4-6正弦函数的图像和性质教学课件
展开
这是一份中职数学基础模块上册4-6正弦函数的图像和性质教学课件,共35页。
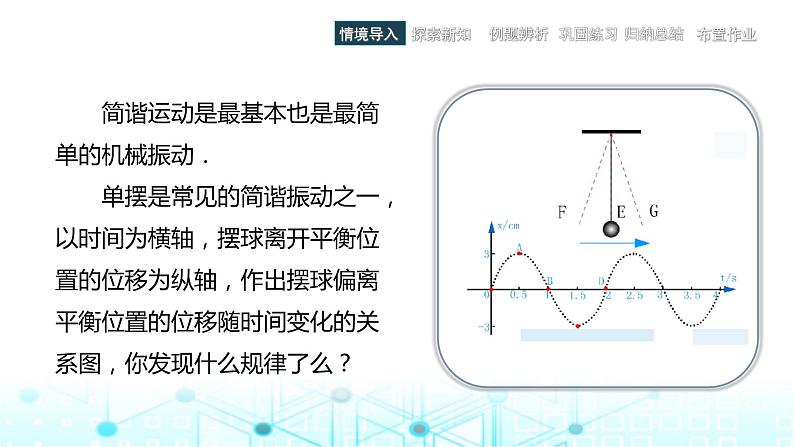
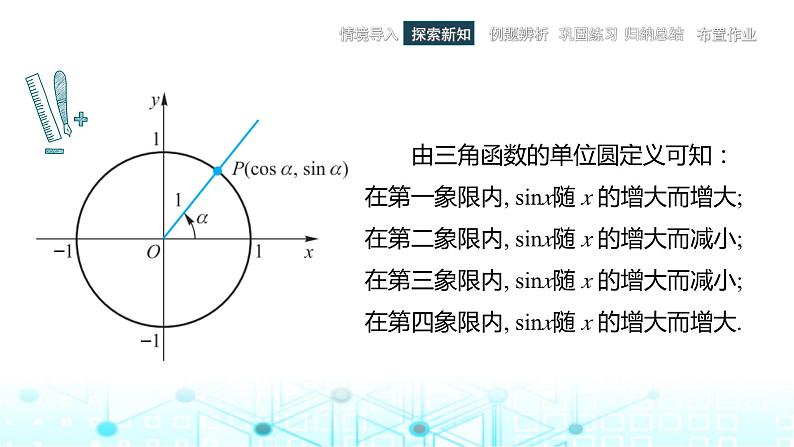
4.6 正弦函数的图像和性质正弦函数的图像4.6.1情境导入探索新知例题辨析巩固练习归纳总结布置作业4.6.1 正弦函数的图像 简谐运动是最基本也是最简单的机械振动. 单摆是常见的简谐振动之一,以时间为横轴,摆球离开平衡位置的位移为纵轴,作出摆球偏离平衡位置的位移随时间变化的关系图,你发现什么规律了么? 由三角函数的单位圆定义可知:在第一象限内, sinx随 x 的增大而增大; 在第二象限内, sinx随 x 的增大而减小; 在第三象限内, sinx随 x 的增大而减小; 在第四象限内, sinx随 x 的增大而增大. 情境导入探索新知例题辨析巩固练习归纳总结布置作业4.6.1 正弦函数的图像情境导入探索新知例题辨析巩固练习归纳总结布置作业 根据单位圆的圆周运动特点, 单位圆上任意一点在圆周上旋转一周就回到原来的位置, 这说明自变量每增加或者减少2π, 正弦函数值将重复出现. 这一现象可以用公式 sin(x+2kπ) = sinx,k∈Z来表示.4.6.1 正弦函数的图像情境导入探索新知例题辨析巩固练习归纳总结布置作业 一般地,对于函数 y=f(x),如果存在一个非零常数T,使得当x取定义域内任意一个值时,都有 f(x+T) =f(x), 则称函数y=f(x)为周期函数.非零常数T为y=f(x)的一个周期. 4.6.1 正弦函数的图像情境导入探索新知例题辨析巩固练习归纳总结布置作业 因此正弦函数y = sinx,x∈R是一个周期函数,2π,4π,6π,…及-2π,-4π,-6π,…都是它的周期,即常数2kπ(k∈Z且k≠0)都是它的周期.如果周期函数y=f(x)的所有周期中存在一个最小的正数 T0,那么这个最小的正数 T0就称为y=f(x)的最小正周期. 显然,2π为正弦函数的最小正周期.4.6.1 正弦函数的图像情境导入探索新知例题辨析巩固练习归纳总结布置作业(1)列表. 把区间[0,2π]分成12等份, 分别求出y=sinx在各分点及区间端点的正弦函数值.4.6.1 正弦函数的图像情境导入探索新知例题辨析巩固练习归纳总结布置作业 根据表中x,y的数值在平面直角坐标系内描点(x, y) ,再用平滑曲线顺次连接各点,就得到正弦函数y=sinx 在 [0,2π]上的图像.(2) 描点作图. 4.6.1 正弦函数的图像情境导入探索新知例题辨析巩固练习归纳总结布置作业 观察函数y=sinx 在 [0,2π]上的图像发现,在确定图像的形状时,起关键作用的点有以下五个,描出这五个点后,正弦函数的图像就基本确定了.4.6.1 正弦函数的图像情境导入探索新知例题辨析巩固练习归纳总结布置作业 因此,在精确度要求不高时,常常先找出这五个关键点,再用光滑的曲线将它们连接起来,就得到[0,2π]上正弦函数的图像简图了,这种作图方法称为五点法.4.6.1 正弦函数的图像情境导入探索新知例题辨析巩固练习归纳总结布置作业 因为正弦函数的周期是2π,所以正弦函数值每隔2π重复出现一次.于是,我们只要将函数y=sinx在 [0,2π]上的图像沿x轴向左或向右平移2kπ(k∈Z),就可得到正弦函数y=sinx,x∈R的图像.正弦函数的图像也称为正弦曲线,它是一条“波浪起伏”的连续光滑曲线.4.6.1 正弦函数的图像例1 利用五点法作出函数y=1+sinx在 [0,2π]上的图像.解 (1)列表. 情境导入探索新知例题辨析巩固练习归纳总结布置作业4.6.1 正弦函数的图像 (2)描点作图.情境导入探索新知例题辨析巩固练习归纳总结布置作业例1 利用五点法作出函数y=1+sinx在 [0,2π]上的图像.解 (1)列表. 根据表中x, y的数值在平面直角坐标系内描点(x,y), 再用平滑曲线顺次连接各点, 就得到函数y=1+sinx在 [0,2π]上的图像.4.6.1 正弦函数的图像练习情境导入探索新知例题辨析巩固练习归纳总结布置作业4.6.1 正弦函数的图像正弦函数的性质4.6.24.6.2 正弦函数的性质情境导入探索新知例题辨析巩固练习归纳总结布置作业 利用研究函数的经验,可否从正弦函数的定义域、值域、周期性、奇偶性和单调性等方面来研究正弦函数的性质呢? 情境导入探索新知例题辨析巩固练习归纳总结布置作业 (1)定义域. 正弦函数的定义域是实数集R.4.6.2 正弦函数的性质情境导入探索新知例题辨析巩固练习归纳总结布置作业(2) 值域. 4.6.2 正弦函数的性质情境导入探索新知例题辨析巩固练习归纳总结布置作业(3) 周期性. 正弦函数是周期为2π的周期函数. 4.6.2 正弦函数的性质情境导入探索新知例题辨析巩固练习归纳总结布置作业(4) 奇偶性. 由图像关于原点对称和诱导公式sin(−x)=−sinx可知,正弦函数是奇函数.4.6.2 正弦函数的性质情境导入探索新知例题辨析巩固练习归纳总结布置作业(5) 单调性. 4.6.2 正弦函数的性质例1 求下列函数的最大值和最小值,并写出取得最大值、最小值时自变量x的集合.情境导入探索新知例题辨析巩固练习归纳总结布置作业4.6.2 正弦函数的性质解 (1) 由正弦函数的性质知,-1≤sinx≤1,所以情境导入探索新知例题辨析巩固练习归纳总结布置作业4.6.2 正弦函数的性质情境导入探索新知例题辨析巩固练习归纳总结布置作业 (2)由正弦函数的性质知,-1≤sinx≤1,所以-2≤-2sinx≤2,-1≤1-2sinx≤3,即-1≤y≤3.故函数的最大值为3,最小值为-1.4.6.2 正弦函数的性质情境导入探索新知例题辨析巩固练习归纳总结布置作业解 根据正弦函数的图像和性质可知:4.6.2 正弦函数的性质情境导入探索新知例题辨析巩固练习归纳总结布置作业解 根据正弦函数的图像和性质可知:4.6.2 正弦函数的性质情境导入探索新知例题辨析巩固练习归纳总结布置作业例4 求函数 的定义域.观察正弦函数y=sinx在[0,2π] 上图像. 发现,在[0,2π]内, 符合题意的x 满足0≤x≤π.由函数的周期性得: 在[0,2π]内, 符合题意的 x 满足0≤x≤π.由函数的周期性得: 2kπ≤x≤π+2kπ(k∈Z),故函数的定义域为{x|2kπ≤x≤π+2kπ,k∈Z}.4.6.2 正弦函数的性质 对含三角函数的函数式求定义域时,除了考虑函数式有意义之外,还要注意三角函数的周期性.情境导入探索新知巩固练习归纳总结布置作业例题辨析4.6.2 正弦函数的性质情境导入例题辨析巩固练习归纳总结布置作业探索新知4.6.2 正弦函数的性质练习 1. 下列等式是否成立?为什么?情境导入探索新知例题辨析巩固练习归纳总结布置作业 2. 求下列函数的值域.4.6.2 正弦函数的性质练习情境导入探索新知例题辨析巩固练习归纳总结布置作业 3.求下列函数的最大值和最小值,并写出取得最大值、最小值时自变量x的集合.4.6.2 正弦函数的性质练习 4.函数y=a+2sinx的最小值是5,求a的值.情境导入探索新知例题辨析巩固练习归纳总结布置作业4.6.2 正弦函数的性质情境导入探索新知例题辨析巩固练习归纳总结布置作业小结4.6 正弦函数的图像和性质作业情境导入探索新知例题辨析巩固练习归纳总结布置作业1.书面作业:完成课后习题和学习与训练;2.查漏补缺:根据个人情况对课题学习复习与回顾;3.拓展作业:阅读教材扩展延伸内容.4.6 正弦函数的图像和性质
4.6 正弦函数的图像和性质正弦函数的图像4.6.1情境导入探索新知例题辨析巩固练习归纳总结布置作业4.6.1 正弦函数的图像 简谐运动是最基本也是最简单的机械振动. 单摆是常见的简谐振动之一,以时间为横轴,摆球离开平衡位置的位移为纵轴,作出摆球偏离平衡位置的位移随时间变化的关系图,你发现什么规律了么? 由三角函数的单位圆定义可知:在第一象限内, sinx随 x 的增大而增大; 在第二象限内, sinx随 x 的增大而减小; 在第三象限内, sinx随 x 的增大而减小; 在第四象限内, sinx随 x 的增大而增大. 情境导入探索新知例题辨析巩固练习归纳总结布置作业4.6.1 正弦函数的图像情境导入探索新知例题辨析巩固练习归纳总结布置作业 根据单位圆的圆周运动特点, 单位圆上任意一点在圆周上旋转一周就回到原来的位置, 这说明自变量每增加或者减少2π, 正弦函数值将重复出现. 这一现象可以用公式 sin(x+2kπ) = sinx,k∈Z来表示.4.6.1 正弦函数的图像情境导入探索新知例题辨析巩固练习归纳总结布置作业 一般地,对于函数 y=f(x),如果存在一个非零常数T,使得当x取定义域内任意一个值时,都有 f(x+T) =f(x), 则称函数y=f(x)为周期函数.非零常数T为y=f(x)的一个周期. 4.6.1 正弦函数的图像情境导入探索新知例题辨析巩固练习归纳总结布置作业 因此正弦函数y = sinx,x∈R是一个周期函数,2π,4π,6π,…及-2π,-4π,-6π,…都是它的周期,即常数2kπ(k∈Z且k≠0)都是它的周期.如果周期函数y=f(x)的所有周期中存在一个最小的正数 T0,那么这个最小的正数 T0就称为y=f(x)的最小正周期. 显然,2π为正弦函数的最小正周期.4.6.1 正弦函数的图像情境导入探索新知例题辨析巩固练习归纳总结布置作业(1)列表. 把区间[0,2π]分成12等份, 分别求出y=sinx在各分点及区间端点的正弦函数值.4.6.1 正弦函数的图像情境导入探索新知例题辨析巩固练习归纳总结布置作业 根据表中x,y的数值在平面直角坐标系内描点(x, y) ,再用平滑曲线顺次连接各点,就得到正弦函数y=sinx 在 [0,2π]上的图像.(2) 描点作图. 4.6.1 正弦函数的图像情境导入探索新知例题辨析巩固练习归纳总结布置作业 观察函数y=sinx 在 [0,2π]上的图像发现,在确定图像的形状时,起关键作用的点有以下五个,描出这五个点后,正弦函数的图像就基本确定了.4.6.1 正弦函数的图像情境导入探索新知例题辨析巩固练习归纳总结布置作业 因此,在精确度要求不高时,常常先找出这五个关键点,再用光滑的曲线将它们连接起来,就得到[0,2π]上正弦函数的图像简图了,这种作图方法称为五点法.4.6.1 正弦函数的图像情境导入探索新知例题辨析巩固练习归纳总结布置作业 因为正弦函数的周期是2π,所以正弦函数值每隔2π重复出现一次.于是,我们只要将函数y=sinx在 [0,2π]上的图像沿x轴向左或向右平移2kπ(k∈Z),就可得到正弦函数y=sinx,x∈R的图像.正弦函数的图像也称为正弦曲线,它是一条“波浪起伏”的连续光滑曲线.4.6.1 正弦函数的图像例1 利用五点法作出函数y=1+sinx在 [0,2π]上的图像.解 (1)列表. 情境导入探索新知例题辨析巩固练习归纳总结布置作业4.6.1 正弦函数的图像 (2)描点作图.情境导入探索新知例题辨析巩固练习归纳总结布置作业例1 利用五点法作出函数y=1+sinx在 [0,2π]上的图像.解 (1)列表. 根据表中x, y的数值在平面直角坐标系内描点(x,y), 再用平滑曲线顺次连接各点, 就得到函数y=1+sinx在 [0,2π]上的图像.4.6.1 正弦函数的图像练习情境导入探索新知例题辨析巩固练习归纳总结布置作业4.6.1 正弦函数的图像正弦函数的性质4.6.24.6.2 正弦函数的性质情境导入探索新知例题辨析巩固练习归纳总结布置作业 利用研究函数的经验,可否从正弦函数的定义域、值域、周期性、奇偶性和单调性等方面来研究正弦函数的性质呢? 情境导入探索新知例题辨析巩固练习归纳总结布置作业 (1)定义域. 正弦函数的定义域是实数集R.4.6.2 正弦函数的性质情境导入探索新知例题辨析巩固练习归纳总结布置作业(2) 值域. 4.6.2 正弦函数的性质情境导入探索新知例题辨析巩固练习归纳总结布置作业(3) 周期性. 正弦函数是周期为2π的周期函数. 4.6.2 正弦函数的性质情境导入探索新知例题辨析巩固练习归纳总结布置作业(4) 奇偶性. 由图像关于原点对称和诱导公式sin(−x)=−sinx可知,正弦函数是奇函数.4.6.2 正弦函数的性质情境导入探索新知例题辨析巩固练习归纳总结布置作业(5) 单调性. 4.6.2 正弦函数的性质例1 求下列函数的最大值和最小值,并写出取得最大值、最小值时自变量x的集合.情境导入探索新知例题辨析巩固练习归纳总结布置作业4.6.2 正弦函数的性质解 (1) 由正弦函数的性质知,-1≤sinx≤1,所以情境导入探索新知例题辨析巩固练习归纳总结布置作业4.6.2 正弦函数的性质情境导入探索新知例题辨析巩固练习归纳总结布置作业 (2)由正弦函数的性质知,-1≤sinx≤1,所以-2≤-2sinx≤2,-1≤1-2sinx≤3,即-1≤y≤3.故函数的最大值为3,最小值为-1.4.6.2 正弦函数的性质情境导入探索新知例题辨析巩固练习归纳总结布置作业解 根据正弦函数的图像和性质可知:4.6.2 正弦函数的性质情境导入探索新知例题辨析巩固练习归纳总结布置作业解 根据正弦函数的图像和性质可知:4.6.2 正弦函数的性质情境导入探索新知例题辨析巩固练习归纳总结布置作业例4 求函数 的定义域.观察正弦函数y=sinx在[0,2π] 上图像. 发现,在[0,2π]内, 符合题意的x 满足0≤x≤π.由函数的周期性得: 在[0,2π]内, 符合题意的 x 满足0≤x≤π.由函数的周期性得: 2kπ≤x≤π+2kπ(k∈Z),故函数的定义域为{x|2kπ≤x≤π+2kπ,k∈Z}.4.6.2 正弦函数的性质 对含三角函数的函数式求定义域时,除了考虑函数式有意义之外,还要注意三角函数的周期性.情境导入探索新知巩固练习归纳总结布置作业例题辨析4.6.2 正弦函数的性质情境导入例题辨析巩固练习归纳总结布置作业探索新知4.6.2 正弦函数的性质练习 1. 下列等式是否成立?为什么?情境导入探索新知例题辨析巩固练习归纳总结布置作业 2. 求下列函数的值域.4.6.2 正弦函数的性质练习情境导入探索新知例题辨析巩固练习归纳总结布置作业 3.求下列函数的最大值和最小值,并写出取得最大值、最小值时自变量x的集合.4.6.2 正弦函数的性质练习 4.函数y=a+2sinx的最小值是5,求a的值.情境导入探索新知例题辨析巩固练习归纳总结布置作业4.6.2 正弦函数的性质情境导入探索新知例题辨析巩固练习归纳总结布置作业小结4.6 正弦函数的图像和性质作业情境导入探索新知例题辨析巩固练习归纳总结布置作业1.书面作业:完成课后习题和学习与训练;2.查漏补缺:根据个人情况对课题学习复习与回顾;3.拓展作业:阅读教材扩展延伸内容.4.6 正弦函数的图像和性质
相关资料
更多








