中考数学复习第四章三角形第13课时线、角、相交线与平行线课件

这是一份中考数学复习第四章三角形第13课时线、角、相交线与平行线课件，共19页。PPT课件主要包含了°28′等内容，欢迎下载使用。

1.(2022·贺州)如图F13-1，直线a，b被直线c所截，下列各组角是同位角的是( )A.∠1与∠2B.∠1与∠3C.∠2与∠3D.∠3与∠4
2.(2022·河池)如图F13-2，平行线a，b被直线c所截，若∠1＝142°，则∠2的度数是( )A.142°B.132°C.58°D.38°
3.(2022·雅安)如图F13-3，已知直线a∥b，直线c与a，b分别交于点A，B.若∠1＝120°，则∠2＝( )A.60°B.120°C.30°D.15°
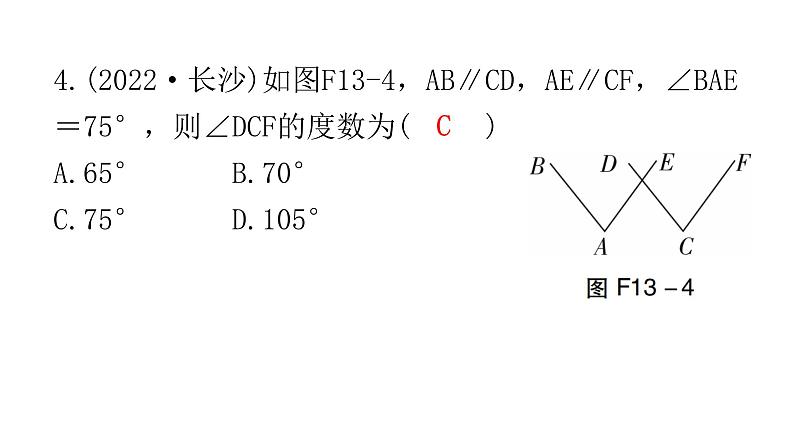
4.(2022·长沙)如图F13-4，AB∥CD，AE∥CF，∠BAE＝75°，则∠DCF的度数为( )A.65°B.70°C.75°D.105°
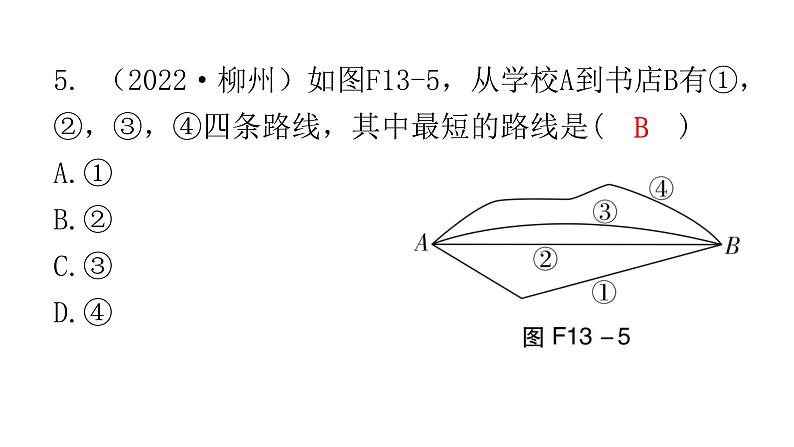
5. （2022·柳州）如图F13-5，从学校A到书店B有①，②，③，④四条路线，其中最短的路线是( )A.① B.② C.③ D.④
6.(2022·连云港)已知∠A的补角为60°，则∠A＝__________.7.(2021·益阳)如图F13-6，AB与CD相交于点O，OE是∠AOC的平分线，且OC恰好平分∠EOB，则∠AOD＝__________°.
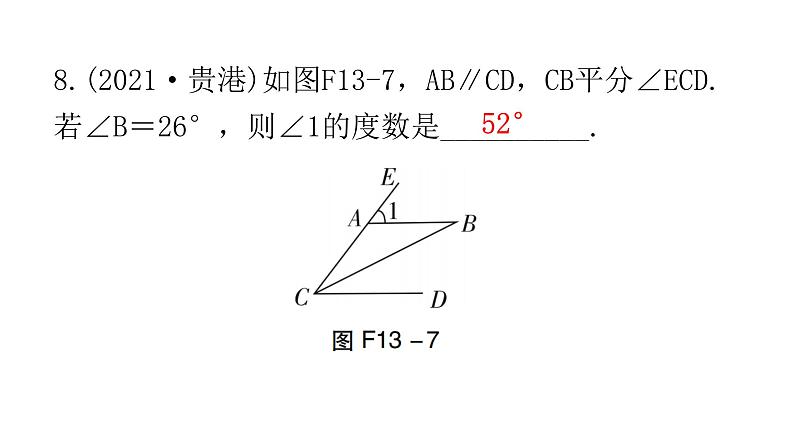
8.(2021·贵港)如图F13-7，AB∥CD，CB平分∠ECD.若∠B＝26°，则∠1的度数是__________.
9. （2021·武汉）如图F13-8，AB∥CD，∠B＝∠D，直线EF与AD，BC的延长线分别交于点E，F.求证：∠DEF＝∠F.
证明：∵AB∥CD，∴∠DCF＝∠B.∵∠B＝∠D，∴∠DCF＝∠D.∴AD∥BC.∴∠DEF＝∠F.
10.(教材改编)如图F13-9，已知∠B＝142°，∠BFE＝38°，∠EFD＝40°，∠D＝140°.求证：AB∥CD.
证明：∵∠B＝142°，∠BFE＝38°，∴∠B+∠BFE＝180°.∴AB∥EF.又∵∠EFD+∠D＝40°+140°＝180°,∴EF∥CD.∴AB∥CD.
11.(2022·湖北)如图F13-10，AB∥CD，直线EF分别交AB，CD于点E，F,∠BEF的平分线交CD于点G.若∠EFG＝52°，则∠EGF＝( )A.128°B.64°C.52°D.26°
12.(2021·阜新)如图F13-11，直线AB∥CD，一块含有30°角的直角三角尺顶点E位于直线CD上，EG平分∠CEF，则∠1的度数为__________.
13.如图F13-12，直线l1，l2，l3被直线l4所截，若l1∥l2，l2∥l3，∠1＝126°32′，则∠2的度数是__________.
14. 如图F13-13，AB∥CD，EF 交 AB 于点 G，交 CD 于点 F，FH 平分 ∠EFD，交 AB 于点 H，∠AGE＝50°，求∠BHF 的度数.
15.(数学文化)我国古代观星，并对星图进行艺术加工可以追溯到公元前，敦煌星图是世界现存古代星图中星数较多、年代最早的星图，绘制于唐代.元朝数学家郭守敬重新观测了二十八星宿(东南西北各七宿，图F13-14①是其中的南方七宿之翼)，编制了当时最先进的历法《授时历》.
小明学习了平行线知识，画出了“南方七宿之翼”的上半部分(如图F13-14②).当a∥b，∠1＝70°，∠2＝25°，∠3＝30°时，根据所学知识，可求得∠4＝__________.
16.(教材改编)如图F13-15，直线AB,CD相交于点O，OM⊥AB.(1)若∠1＝∠2，求∠NOD的度数；(2)若∠AOD＝3∠1，求∠AOC和∠MOD的度数.
解：(1)∵OM⊥AB，∴∠AOM＝∠BOM＝90°.∴∠1+∠AOC＝90°.∵∠1＝∠2，∴∠2+∠AOC＝90°，即∠CON＝90°.∴∠NOD＝180°－∠CON＝180°－90°＝90°.