中考数学复习第四章三角形第13课时线、角、相交线与平行线课件

这是一份中考数学复习第四章三角形第13课时线、角、相交线与平行线课件，共59页。PPT课件主要包含了课前循环练，新课标，考点梳理，广东中考，高分击破，中考演练，命题趋势，限时5分钟，两点确定一条直线，两点之间线段最短等内容，欢迎下载使用。

1. （广东真题）下列式子是完全平方式的是（ ）A. a2+ab+b2B. a2+2a+2C. a2-2b+b2D. a2+2a+1
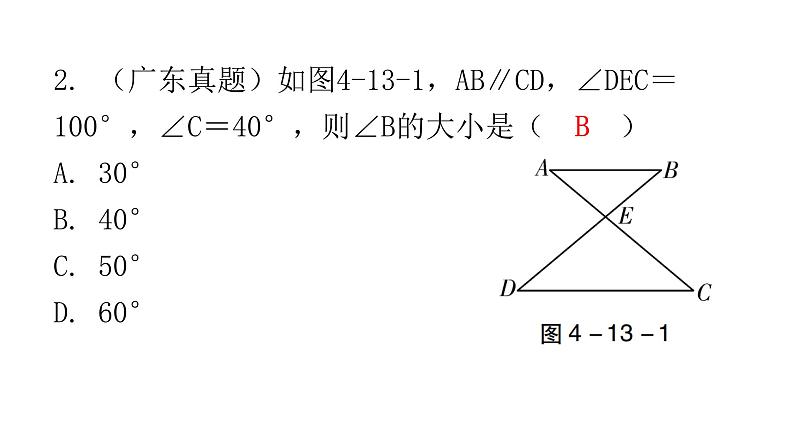
2. （广东真题）如图4-13-1，AB∥CD，∠DEC＝100°，∠C＝40°，则∠B的大小是（ ）A. 30°B. 40°C. 50°D. 60°
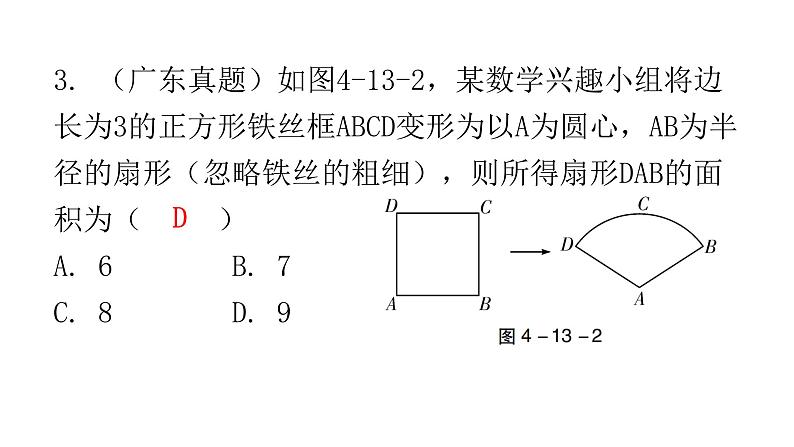
3. （广东真题）如图4-13-2，某数学兴趣小组将边长为3的正方形铁丝框ABCD变形为以A为圆心，AB为半径的扇形（忽略铁丝的粗细），则所得扇形DAB的面积为（ ）A. 6B. 7C. 8D. 9
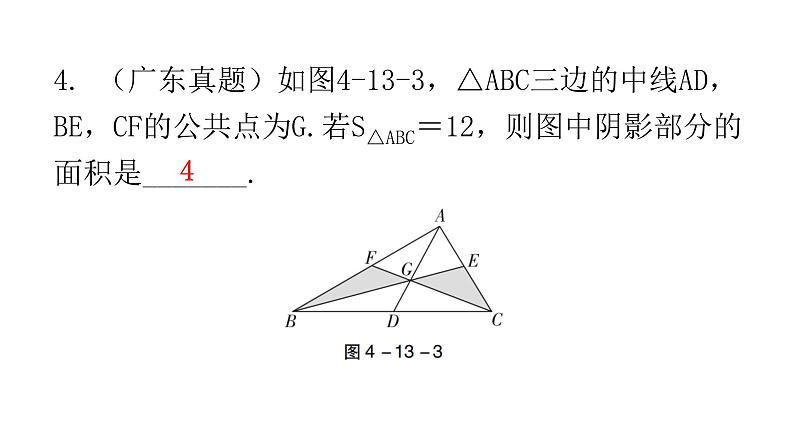
4. （广东真题）如图4-13-3，△ABC三边的中线AD，BE，CF的公共点为G.若S△ABC＝12，则图中阴影部分的面积是_______.
5. （广东真题）在一个不透明的盒子中，有五个完全相同的小球，把它们分别标号为1，2，3，4，5，随机摸出一个小球，摸出的小球标号为偶数的概率是___________.
(1)点、线、面、角①通过实物和模型，了解从物体抽象出来的几何体、平面、直线和点等概念. ②会比较线段的长短，理解线段的和、差，以及线段中点的意义. ③掌握基本事实：两点确定一条直线. ④掌握基本事实：两点之间线段最短.
⑤理解两点间距离的意义，能度量和表达两点间的距离. ⑥理解角的概念，能比较角的大小；认识度、分、秒等角的度量单位，能进行简单的单位换算，会计算角的和、差. ⑦了解角平分线的概念（新增）.
(2)相交线与平行线①理解对顶角、余角、补角等概念，探索并掌握对顶角相等、同角（或等角）的余角相等、同角（或等角）的补角相等的性质. ②理解垂线、垂线段等概念，能用三角板或量角器过一点画已知直线的垂线. ③掌握基本事实：在同一平面内，过一点有且只有一条直线与已知直线垂直.
④理解点到直线的距离的意义，能度量点到直线的距离. ⑤识别同位角、内错角、同旁内角. ⑥理解平行线的概念. ⑦掌握平行线基本事实Ⅰ：过直线外一点有且只有一条直线与这条直线平行. ⑧掌握平行线基本事实Ⅱ：两条直线被第三条直线所截，如果同位角相等，那么这两条直线平行.
⑨探索并证明平行线的判定定理：两条直线被第三条直线所截，如果内错角相等（或同旁内角互补），那么这两条直线平行. ⑩掌握平行线的性质定理Ⅰ：两条平行直线被第三条直线所截，同位角相等. *了解定理的证明. 探索并证明平行线的性质定理Ⅱ：两条平行直线被第三条直线所截，内错角相等（或同旁内角互补）.
能用三角板和直尺过已知直线外一点画这条直线的平行线. 了解平行于同一条直线的两条直线平行.
（学生预习完成，教师课堂精准点拨）
人教：七上第四章 几何图形初步； 七下第五章 相交线与平行线北师：七上第四章 基本平面图形； 七下第二章 相交线与平行线 八上第七章 平行线的证明
1. 直线、射线与线段（1）直线___ ___端点，射线有1个端点，线段有_____个端点．（2）经过____ __有且只有一条直线，简述为两点确定一条直线．
（3）两点之间的所有连线中，__________最短，简述为两点之间线段最短．（4）两点之间线段的___________，叫做这两点之间的距离
例1. （1）木匠师傅锯木料时，一般先在木板上画出两个点，然后过这两点弹出一条墨线，其依据的数学原理是___________________；（2）如图4-13-4，从公园甲到公园乙的三条路线中，最短的是______（填序号），这是因为___________________．
2. 角的相关概念（1）由两条具有公共端点的________所组成的图形叫做角．两条射线的公共端点是这个角的顶点．（2）按照角的大小，角可分为锐角、___________、___________、平角和周角．（3）1周角=2平角=4直角=360°．
（4）1°=60′，1′=60″．（5）余角、补角：如果两个角的和是90°，那么称这两个角互为余角，同角或等角的余角___________；如果两个角的和是180°，那么称这两个角互为补角，同角或等角的补角___________
例2. （1）计算：50°-15°30′=___________；（2）已知 ∠A=28°，则 ∠A 的余角的度数为___________，∠A 的补角的度数为___________．
3. 角的平分线从一个角的顶点引出的一条射线，把这个角分成两个__________的角，这条射线叫做这个角的平分线
例3. 如图4-13-5，在∠AOB 中，OD 是 ∠BOC 的平分线，OE 是 ∠AOC 的平分线.若 ∠AOB=140°，则 ∠EOD=_________.
4. 对顶角对顶角___________. 互为对顶角的两个角相等，但相等的两个角不一定是对顶角
例4. 如图4-13-6是对顶角量角器，用它测量角的原理是______ _____.
5. 垂直性质（1）平面内，过一点___________一条直线与已知直线垂直. （2）直线外一点与直线上各点连接的所有线段中，___________最短
例5. 如图4-13-7，村庄 A 到公路 BC 的最短距离是 AD 的长，其根据的数学原理是________ ___.
6. 三线八角（如图4-13-8）（1）同位角：∠1 与 ∠5，∠2 与 ∠6，∠4 与_________，∠3 与_________.（2）内错角：∠2 与_________，∠3 与 ∠5. （3）同旁内角：∠3 与 ∠8，∠2 与___________
例6. 如图4-13-9，已知直线 a∥b，∠1=70°，则 ∠2=___________.
7. 平行线的性质与判定（如图4-13-10）（1）同位角___________⇔两直线平行.判定：∵∠1=∠2，∴l1∥l2．性质：∵l1∥l2，∴∠1=∠2.（2）内错角相等⇔两直线___________.判定：∵∠2=∠3，∴l1∥l2．性质：∵l1∥l2，∴∠2=∠3.
（3）同旁内角___________⇔两直线平行．判定：∵∠2+∠4=180°，∴l1∥l2．性质：∵l1∥l2，∴∠2+∠4=180°
例7. 如图4-13-11，填空：（1）由∠ABD=∠CDB，得________∥________；（2）由∠CAD=∠ACB，得________∥________；（3）由∠CBA+∠BAD=180°，得________∥________.
8. 平行公理（1）过直线外一点，___________一条直线与这条直线平行. （2）平行于同一条直线的两条直线___________
例8. 如图4-13-12，已知 AB∥CD，求证：∠BED=∠B+∠D. （完成证明过程）证明：过点E作 EF∥AB. ∴∠1=__________.∵AB∥CD（已知），∴EF∥CD（_________________________________）. ∴∠2=__________. ∴∠BED=∠1+∠2=∠B+∠D.
平行于同一条直线的两条直线平行
1. （2022·广东，平行线的性质）如图4-13-13，直线a∥b，∠1＝40°，则∠2＝（ ）A. 30°B. 40°C. 50°D. 60°
2. （2019·广东，平行线的性质）如图4-13-14，已知a∥b，∠1＝75°，则∠2＝___________.
1. （2022·武汉）如图4-13-15，在四边形ABCD中，AD∥BC，∠B＝80°. （1）求∠BAD的度数；（2）AE平分∠BAD交BC于点E，∠BCD＝50°. 求证：AE∥DC.
（1）解：∵AD∥BC，∴∠B+∠BAD＝180°. ··2分（利用“两直线平行，同旁内角互补”得2分）∵∠B＝80°，∴∠BAD＝100°.····3分（求出∠BAD的度数得1分）
温馨提示：温馨提示：此类考题常见于广东省中考数学试卷的第18小题，分值一般为8分，答题时要注意书写格式，分步书写，慢做会求全对，评卷老师是分步给分的哦！
【典型错例】不理解和未掌握平行线的判定与性质的运用
2. 如图4-13-16，在△ABC中，已知∠1+∠2=180°，∠3=∠B， 试判断DE与BC的位置关系，并说明理由.
解：DE∥BC.理由如下.∵∠1＋∠2=180°，∠1=∠4，∴∠4+∠2=180°. ∴EF∥DB(同旁内角互补，两直线平行). ∴∠3+∠BDE=180°(两直线平行, 同旁内角互补). ∵∠3=∠B，∴∠B+∠BDE=180°. ∴DE∥BC(同旁内角互补，两直线平行).
【变式考点】平行线的判定与性质的综合运用
3. （教材改编）将一副三角板拼成如图4-13-17所示的图形，过点C作CF平分∠DCE交DE于点F. （1）求证：CF∥AB；（2）求∠DFC的度数.
【创新考点】平行线的判定与性质的运用创新
（2）∵∠α+∠β＝50°+130°＝180°，∴AB∥EF. 又∵CD∥EF，∴AB∥CD. ∴∠C+∠CAB＝180°. ∵AC⊥AE，∴∠CAE＝90°. ∴∠CAB=∠CAE+∠α=90°+50°=140°.∴∠C=180°-∠CAB＝180°-140°＝40°.
一、选择题1. （2022·自贡）如图4-13-19，直线AB，CD相交于点O，若∠1＝30°，则∠2的度数是（ ）A. 30°B. 40°C. 60°D. 150°
2. （2022·云南）如图4-13-20，已知直线c与直线a，b都相交. 若a∥b，∠1＝85°，则∠2＝（ ）A. 110°B. 105°C. 100°D. 95°
3. （2022·滨州）如图4-13-21，在弯形管道ABCD中，若AB∥CD，拐角∠ABC＝122°，则∠BCD的大小为（ ）A. 58°B. 68°C. 78°D. 122°
4. （2022·河南）如图4-13-22，直线AB，CD相交于点O，EO⊥CD，垂足为O. 若∠1＝54°，则∠2的度数为（ ）A. 26°B. 36°C. 44°D. 54°
5. （2022·黔东南州）一块直角三角板按如图4-13-23所示的方式放置在一张长方形纸条上，若∠1＝28°，则∠2的度数为（ ）A. 28°B. 56°C. 36°D. 62°
二、填空题6. （2022·玉林）已知：α＝60°，则α的余角是_________. 7. （2022·湖北）如图4-13-24，直线a∥b，直线c与直线a，b相交.若∠1＝54°，则∠3＝___________.
8. （2022·眉山）如图4-13-25，已知a∥b，∠1＝110°，则∠2的度数为___________.
三、解答题9. （教材改编）如图4-13-26，∠1＝∠2，∠3＝∠4，∠E＝90°.求证：AB∥CD.
证明：∵∠E＝90°，∴∠1+∠3＝90°. ∵∠1＝∠2，∠3＝∠4，∴∠1+∠2+∠3+∠4＝180°. ∴AB∥CD.
10. （教材改编）如图4-13-27，已知AC∥DE，CD∥EF，CD平分∠ACB. 求证：（1）∠DCB＝∠CDE；（2）EF平分∠DEB.
证明：（1）∵AC∥DE，∴∠ACD＝∠CDE. ∵CD平分∠ACB，∴∠ACD＝∠DCB. ∴∠DCB＝∠CDE. （2）∵DC∥EF，∴∠DCB＝∠FEB，∠DEF＝∠CDE. 又由（1）知∠DCB＝∠CDE，∴∠FEB=∠DEF. ∴EF平分∠DEB.
（运算能力；几何直观；推理能力；创新意识）如图4-13-28，已知AB∥CD∥EF．（1）若∠x=60°，∠y=150°，求∠z的度数；（2）猜想∠x，∠y，∠z三者之间的关系并加证明．