2022-2023学年云南省曲靖市富源县高二下学期期末检测数学试题含答案

2022-2023学年云南省曲靖市富源县高二下学期期末检测数学试题

一、单选题

1．复数的虚部为（    ）

A．4 B． C． D．

【答案】B

【分析】根据复数的乘法运算化简复数，即可由虚部的定义求解.

【详解】，故虚部为，

故选：B

2．已知集合，若，则的取值集合为（    ）

A． B． C． D．

【答案】D

【分析】根据空集和非空集两种情况即可求解.

【详解】由可得，若时，则，

若时，则由可得或，故或，则或，

故的取值集合为，

故选:D

3．“”是“”的（    ）

A．充分不必要条件 B．必要不充分条件

C．充要条件 D．既不充分又不必要条件

【答案】A

【分析】根据充分必要条件的定义判断．

【详解】时，成立，是充分的，但时，，不满足，必要性不满足，因此是充分不必要条件．

故选：A．

4．已知是两条不重合的直线，是两个不重合的平面，下列结论正确的是（    ）

A．若，则 B．若，则

C．若，则 D．若，则

【答案】C

【分析】对于A，根据可能平行、可能相交且不垂直判断；对于B，根据可能平行、可能相交且不垂直、异面且不垂直判断；对于C，根据线面垂直的性质定理判断；对于D，根据或异面判断．

【详解】对于A，，则可能平行、可能相交且不垂直，故A不正确；

对于B，，则可能平行、可能相交且不垂直、可能异面且不垂直，故B不正确；

对于C，若，根据线面垂直的性质定理可知，故C正确；

对于D，若，则或异面，故D不正确．

故选：C．

5．已知函数在上单调递增，则a的取值范围为（    ）

A． B．

C．  D．

【答案】C

【分析】求出函数的导数，由题意可得在上恒成立，由此参变分离，结合二次函数的最值即可求得答案.

【详解】因为，所以，

由在上单调递增，得在上恒成立，

即在上恒成立，，

即在上恒成立，

当时，二次函数取到最大值，

故，即a的取值范围为，

故选：C

6．已知抛物线的焦点到其准线的距离为是抛物线上一点，若，则的最小值为（    ）

A．8 B．6 C．5 D．4

【答案】D

【分析】由抛物线的焦点坐标求得，设在准线上的射影为，利用抛物线的定义进行转化后易得最小值．

【详解】由焦点到其准线的距离为得；

设在准线上的射影为如图,

则，

当且仅当共线时取得等号．所以所求最小值是4．

故选：D．

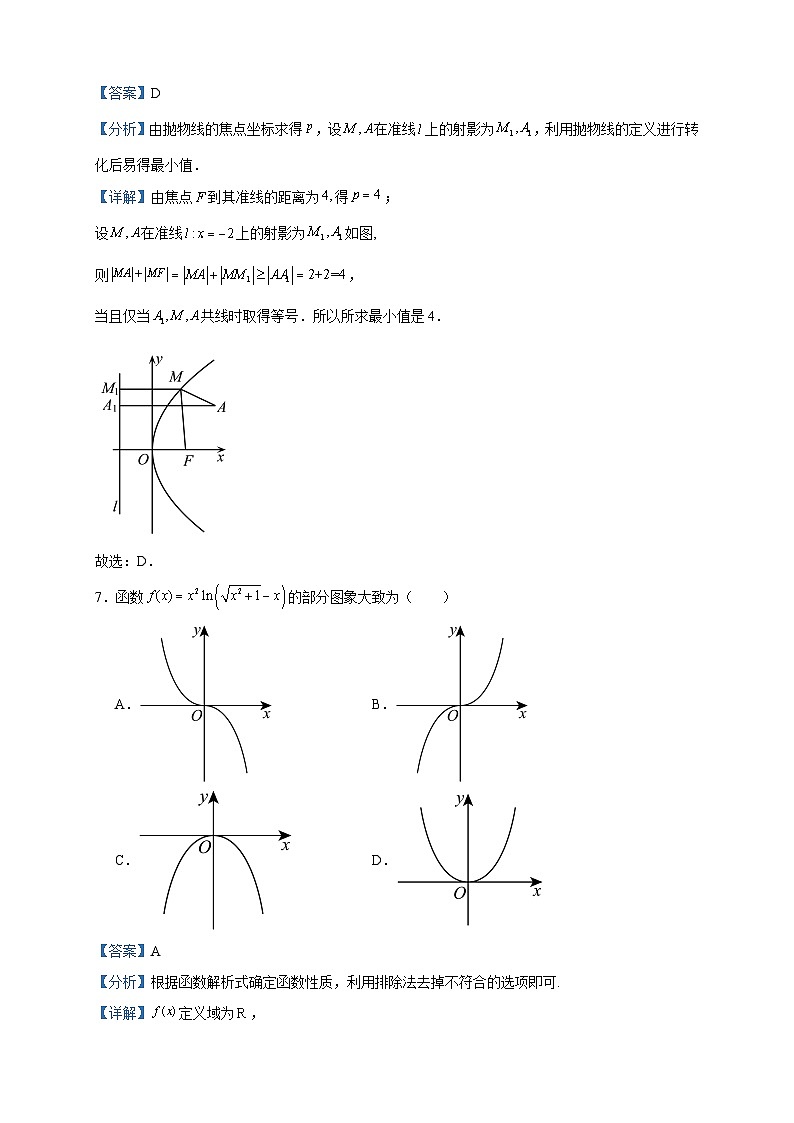
7．函数的部分图象大致为（    ）

A． B．  

C．   D．  

【答案】A

【分析】根据函数解析式确定函数性质，利用排除法去掉不符合的选项即可.

【详解】定义域为，

因为，

所以是奇函数，排除C，D．

当时，，则，，所以，排除B．

故选：A．

8．弘扬国学经典，传承中华文化，国学乃我中华民族五千年留下的智慧精髓，其中“五经”是国学经典著作，“五经”指《诗经》《尚书》《礼记》《周易》《春秋》．小明准备学习“五经”，现安排连续四天进行学习且每天学习一种，每天学习的书都不一样，其中《诗经》与《礼记》不能安排在相邻两天学习，《周易》不能安排在第一天学习，则不同安排的方式有（    ）

A．32种 B．48种

C．56种 D．68种

【答案】D

【分析】利用排列组合分别讨论不排《周易》，排《周易》且《诗经》与《礼记》都安排，排《周易》且《诗经》与《礼记》只安排一个，三种情况，再利用分类加法计数原理将所有情况相加即可.

【详解】①若《周易》不排，先将《诗经》与《礼记》以外的另外2种排列，

再将《诗经》与《礼记》插空，则共有种安排方式．

②若排《周易》且《诗经》与《礼记》都安排，

在《尚书》和《春秋》中先选1种，然后将《诗经》与《礼记》以外的另外2种排列，

再将《诗经》与《礼记》插空，减去将《周易》排在第一天的情况即可，

共有种安排方式；

③若排《周易》且《诗经》与《礼记》只安排一个，

先在《诗经》与《礼记》中选1种，然后将《周易》排在后三天的一天，

最后将剩下的3种书全排列即可，

共有种安排方式．

所以共有种安排方式．

故选：D

二、多选题

9．已知一组数据：的平均数为，标准差为，则（    ）

A．另一组数据：的平均数为

B．另一组数据：的平均数为

C．另一组数据：的标准差为

D．另一组数据：的标准差为

【答案】AC

【分析】根据平均数和标准差的性质即可求解.

【详解】的平均数为,的方差为，标准差为，

故AC正确，BD错误，

故选：AC

10．已知函数的部分图象如图所示，则下列说法正确的是（    ）

A．的最小正周期为

B．的单调递增区间为

C．的图象关于直线对称

D．的图象可由函数的图象向左平移个单位长度得到

【答案】AC

【分析】根据图象确定周期可判断A，由周期求出，利用特殊值求出得出函数，根据正弦函数的单调性判断B；根据正弦型函数的对称轴判断C；由三角函数的图象平移可判断D.

【详解】由图象可知，，，故的最小正周期为，故A正确；

所以，得.

又，

即，所以，，所以，，

又因为，所以，所以，

令，

解得，所以的单调递增区间为，故B错误；

因为，所以的图象关于直线对称，故C正确；

将函数的图象向左平移个单位得到，故D错误.

故选：AC

11．已知双曲线：的右焦点到渐近线的距离为，为上一点，下列说法正确的是（    ）

A．的离心率为

B．的最小值为

C．若，为的左、右顶点，与，不重合，则直线，的斜率之积为

D．设的左焦点为，若的面积为，则

【答案】ACD

【分析】根据题意列关于的等式，从而可得双曲线的方程，计算离心率，的最小值，结合动点满足的方程，列式计算，在焦点三角形中，由双曲线的定义，余弦定理以及三角形面积公式列式即可计算出.

【详解】由已知可得，，所以，

则的方程为，离心率为，A正确；

因为的最小值为，所以B错误；

设，则，，

，所以C正确；

设，由

可得，得，

则，所以D正确．

故选：ACD

12．已知，则（    ）

A． B． C． D．

【答案】ABC

【分析】构造函数，求导后可得在单调递增，则可得，构造函数，求导后可得在单调递减，则可得，从而可得结论.

【详解】令，则，

当时，，所以在单调递增，

所以，则，

所以，所以，

令，则，

所以在单调递减，

所以，则，即，所以，

所以

故选：ABC.

【点睛】关键点点睛：此题考查对数式，指数式比较大小，考查导数的应用，解题的关键是合理构造函数，利用导数判断函数的单调性，然后利用函数的单调性比较大小，属于较难题.

三、填空题

13．已知向量，则         ．

【答案】

【分析】直接利用平面向量的数量积坐标运算求解即可.

【详解】因为向量，

所以，

故答案为：

14．圆心在第二象限，半径为3，且与两条坐标轴均相切的圆的标准方程为         ．

【答案】

【分析】根据圆心和半径即可写出标准方程.

【详解】由题意可得所求的圆半径为3,由于两条坐标轴均相切，且圆心在第二象限，故圆心为，，

圆的标准方程为；

故答案为：

15．等差数列的前项和为，若，，则     ．

【答案】15

【分析】根据等差数列的性质得到，求出答案.

【详解】设，由等差数列的性质可得，

又，则，解得．

故答案为：15

16．正四面体的表面积为，正四面体外接球的表面积为，则         ．

【答案】

【分析】根据球的表面积以及棱锥的表面积公式即可求解.

【详解】把正四面体放入正方体中，如图所示：

该四面体可以看成棱长为的正方体六个面对角线组成的正四面体，

所以正四面体的外接球即为棱长为的正方体的外接球，

所以外接球的半径为，则外接球的表面积，

正四面体的棱长为，所以表面积为，

所以，

故答案为：

四、解答题

17．在等差数列中，．

(1)求的通项公式；

(2)求数列的前项和．

【答案】(1)

(2)

【分析】（1）根据等差数列基本量的计算即可求解，

（2）由裂项求和即可求解.

【详解】（1）设等差数列的首项和公差分别为，

则由得且，

解得,

所以，

（2）由于，

所以

18．已知的内角的对边分别为，且．

(1)求；

(2)若，求面积的最大值．

【答案】(1)

(2)

【分析】（1）根据正弦定理边角化，结合辅助角公式以及三角函数的性质就可求解，

（2）由余弦定理以及不等式可得的最大值，即可由面积公式求解.

【详解】（1）由正弦定理可得所以

进而可得，由于,所以

（2）由余弦定理可得，

由于，所以，当且仅当等号成立，

故的最大值为12，故面积为，

故面积的最大值为

19．如图，在四棱锥中，底面是直角梯形，，，，，底面是的中点，.

(1)证明：平面平面.

(2)若直线与平面所成角的正弦值为，且，求平面与平面夹角的余弦值.

【答案】(1)证明见解析

(2)

【分析】（1）由余弦定理求出，由勾股定理逆定理得到线线垂直，进而得到线面垂直，证明出面面垂直；

（2）建立空间直角坐标系，设出点的坐标，利用线面角的大小列出方程，求出，从而利用空间向量求出面面角的余弦值

【详解】（1）因为底面平面，所以.

因为，所以.

又，

所以，

则，故.

因为，平面，所以平面.

又平面，所以平面平面.

（2）取中点，连接，

因为底面是直角梯形，，，，，

所以，

因为底面，平面，所以，

以为坐标原点，所在直线分别为轴，建立如图所示的空间直角坐标系，

则，

设，则，

.

设平面的法向量为，

则，解得，

令，得，故.

因为直线与平面所成角的正弦值为，

所以，

解得或（舍去），则，

则.

设平面的法向量为，

则，

令，则，得.

，

故平面与平面夹角的余弦值为.

20．投壶是中国古代士大夫宴饮时做的一种投掷游戏，也是一种礼仪，在战国时期较为盛行，尤其是在唐朝，得到了发扬光大．投壶是把箭向壶里投，投中多的为胜．某校开展“健康体育节”活动，其间甲、乙两人轮流进行定点投壶比赛（每人各投一次为一轮，且不受先后顺序影响），在相同的条件下，甲、乙两人每轮在同一位置，每人投一次．若两人有一人投中，投中者得分，未投中者得分；若两人都投中，两人均得分；若两人都未投中，两人均得分．设甲每次投中的概率为，乙每次投中的概率为，且各次投壶互不影响．

(1)用表示经过第轮投壶累计得分后甲得分等于乙得分的概率，求与；

(2)经过轮投壶，记甲、乙的得分之和为，求的分布列和数学期望．

【答案】(1)，

(2)分布列答案见解析，

【分析】（1）根据独立事件的概率乘法公式结合互斥事件的概率加法公式可求得、的值；

（2）分析可知随机变量的可能取值有、、，计算出随机变量在不同取值下的概率，可得出随机变量的分布列，进而可求得的值.

【详解】（1）解：由题意可知，，

.

（2）解：由题意可知，随机变量的可能取值有、、，

，

，

，

所以，随机变量的分布列如下表所示：

因此，.

21．已知函数.

(1)当时，求的极值；

(2)若在上恰有1个极值点，求的取值范围.

【答案】(1)极小值为，无极大值

(2).

【分析】（1）根据题意，求导即可得到其极值；

（2）根据题意，将极值点转化为函数零点问题，然后利用导数研究，即可得到结果.

【详解】（1）因为，所以，.

令，得或，且当时，，

当时，，故的单调递减区间为，单调递增区间为.

从而的极小值为，无极大值.

（2）因为，所以.

因为在上恰有1个极值点，所以在上恰有一个变号零点.

令，则，

显然在上单调递增，且，所以在上恒成立，

则在上单调递增.

要使在上恰有一个变号零点，则，

即，故的取值范围为.

22．已知椭圆的左、右焦点分别为、，离心率为，且椭圆上的点到焦点的距离的最大值为．

(1)求椭圆的方程．

(2)设、是椭圆上关于轴对称的不同两点，在椭圆上，且点异于、两点，为原点，直线交轴于点，直线交轴于点，试问是否为定值？若为定值，求出这个定值；若不是定值，请说明理由．

【答案】(1)

(2)

【分析】（1）求出椭圆上任意一点到其焦点距离的最大值，结合离心率可得出、的值，进而求出的值，由此可得出椭圆的标准方程；

（2）设点，，，，，将直线的方程与椭圆的方程联立，求出，同理可得出的另外一个表达式，利用等量关系可得出关于、的等式，讨论、两种情形，可求出的定值.

【详解】（1）解：设点为椭圆上任意一点，其中，易知点，

，

所以，椭圆上的点到焦点的距离的最大值为，

又因为椭圆的离心率为，

所以，，，则，

因此，椭圆的标准方程为.

（2）解：设点，，，，，

则直线的方程为，直线的方程为，

联立，消去并整理可得，

因为点在椭圆上，则直线与椭圆必有公共点，

所以，，

同理可得

所以，，

所以，，

化简可得，

当时，则，此时，；

当时，、、三点重合，此时，.

综上所述，，即为定值.

【点睛】方法点睛：求定值问题常见的方法有两种：

（1）从特殊入手，求出定值，再证明这个值与变量无关；

（2）直接推理、计算，并在计算推理的过程中消去变量，从而得到定值．