中考数学二轮专项复习——动点、最值问题(压轴题)（含答案）

这是一份中考数学二轮专项复习——动点、最值问题(压轴题)（含答案），共25页。

中考数学二轮专项复习——动点、最值问题（压轴题）
1． （眉山中考 第26题 11分）如图1，在平面直角坐标系中，抛物线y＝﹣x2+bx+c经过点A（﹣5，0）和点B（1，0）.
（1）求抛物线的解析式及顶点D的坐标；
（2）点P是抛物线上A、D之间的一点，过点P作PE⊥x轴于点E，PG⊥y轴，交抛物线于点G.过点G作GF⊥x轴于点F.当矩形PEFG的周长最大时，求点P的横坐标；
B
A
C
O
D
E
F
G
P
y
x
图1
图2
A
B
C
D
y
x
M
N
O
（3）如图2，连接AD、BD，点M在线段AB上（不与A、B重合），作∠DMN＝∠DBA, MN交线段AD于点N，是否存在这样点M，使得△DMN为等腰三角形？若存在，求出AN的长；若不存在，请说明理由.












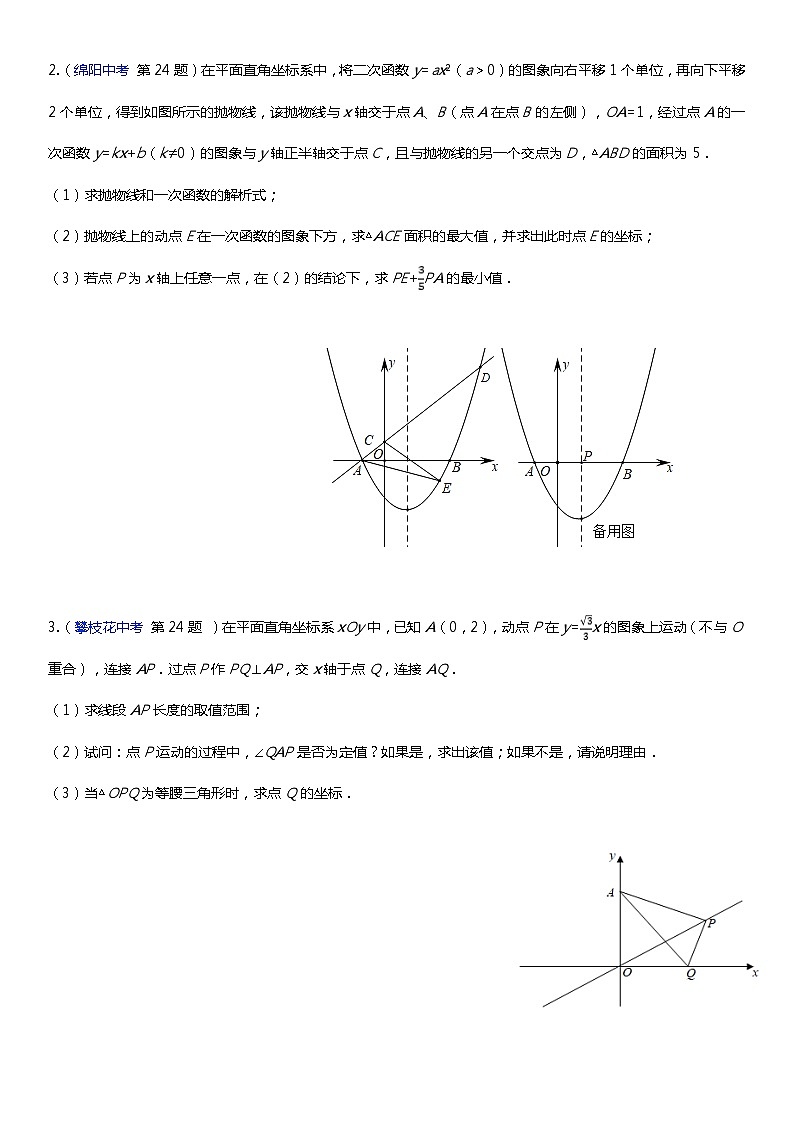
2.（绵阳中考 第24题）在平面直角坐标系中，将二次函数y=ax2（a＞0）的图象向右平移1个单位，再向下平移2个单位，得到如图所示的抛物线，该抛物线与x轴交于点A、B（点A在点B的左侧），OA=1，经过点A的一次函数y=kx+b（k≠0）的图象与y轴正半轴交于点C，且与抛物线的另一个交点为D，△ABD的面积为5．
（1）求抛物线和一次函数的解析式；
（2）抛物线上的动点E在一次函数的图象下方，求△ACE面积的最大值，并求出此时点E的坐标；
（3）若点P为x轴上任意一点，在（2）的结论下，求PE+PA的最小值．


3.（攀枝花中考 第24题 ）在平面直角坐标系xOy中，已知A（0，2），动点P在y=x的图象上运动（不与O重合），连接AP．过点P作PQ⊥AP，交x轴于点Q，连接AQ．
（1）求线段AP长度的取值范围；
（2）试问：点P运动的过程中，∠QAP是否为定值？如果是，求出该值；如果不是，请说明理由．
（3）当△OPQ为等腰三角形时，求点Q的坐标．
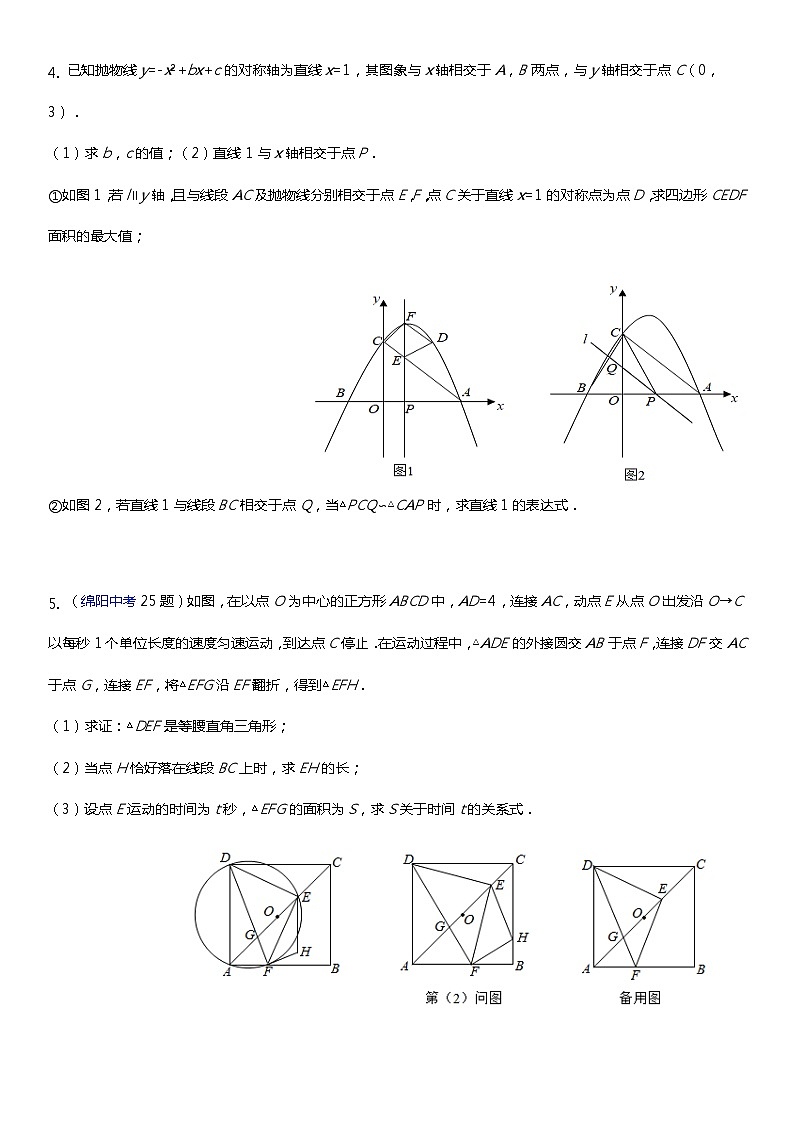
4. 已知抛物线y=-x2+bx+c的对称轴为直线x=1，其图象与x轴相交于A，B两点，与y轴相交于点C（0，3）．
（1）求b，c的值；（2）直线1与x轴相交于点P．
①如图1，若l∥y轴，且与线段AC及抛物线分别相交于点E，F，点C关于直线x=1的对称点为点D，求四边形CEDF面积的最大值；
②如图2，若直线1与线段BC相交于点Q，当△PCQ∽△CAP时，求直线1的表达式．

5. （绵阳中考25题）如图，在以点O为中心的正方形ABCD中，AD=4，连接AC，动点E从点O出发沿O→C以每秒1个单位长度的速度匀速运动，到达点C停止．在运动过程中，△ADE的外接圆交AB于点F，连接DF交AC于点G，连接EF，将△EFG沿EF翻折，得到△EFH．
（1）求证：△DEF是等腰直角三角形；
（2）当点H恰好落在线段BC上时，求EH的长；
（3）设点E运动的时间为t秒，△EFG的面积为S，求S关于时间t的关系式．


6．（资阳中考 第24题）如图，在平面直角坐标系xOy中，已知抛物线y＝ax2﹣2x+c与直线y＝kx+b都经过A（0，﹣3）、B（3，0）两点，该抛物线的顶点为C．
（1）求此抛物线和直线AB的解析式；
（2）设直线AB与该抛物线的对称轴交于点E，在射线EB上是否存在一点M，过M作x轴的垂线交抛物线于点N，使点M、N、C、E是平行四边形的四个顶点？若存在，求点M的坐标；若不存在，请说明理由；
（3）设点P是直线AB下方抛物线上的一动点，当△PAB面积最大时，求点P的坐标，并求△PAB面积的最大值．


7. 在矩形ABCD中，连结AC，点E从点B出发，以每秒1个单位的速度沿着B→A→C的路径运动，运动时间为t（秒）．过点E作EF⊥BC于点F，在矩形ABCD的内部作正方形EFGH．
（1）如图，当AB＝BC＝8时，
①若点H在△ABC的内部，连结AH、CH，求证：AH＝CH；
②当0＜t≤8时，设正方形EFGH与△ABC的重叠部分面积为S，求S与t的函数关系式；
（2）当AB＝6，BC＝8时，若直线AH将矩形ABCD的面积分成1：3两部分，求t的值．




8.（金华中考 第24题 ）如图，在等腰Rt△ABC中，∠ACB=90°，AB=.点D，E分别在边AB，BC上，将线段ED绕点E按逆时针方向旋转90°得到EF.
（1）如图1，若AD=BD，点E与点C重合，AF与DC相交于点O,求证：BD=2DO.
（2）已知点G为AF的中点.
①如图2，若AD=BD，CE=2，求DG的长.
图1 图2 图3
D
A
(E)
B
C
F
F
G
D
A
E
B
C
F
G
D
A
E
B
C

O
②若AD=6BD,是否存在点E,使得△DEG是直角三角形？若存在，求CE的长；若不存在，试说明理由.






9.（资阳中考 第24题13分）如图，抛物线y＝﹣x2+bx+c过点A（3，2），且与直线y＝﹣x+交于B、C两点，点B的坐标为（4，m）．
（1）求抛物线的解析式；
（2）点D为抛物线上位于直线BC上方的一点，过点D作DE⊥x轴交直线BC于点E，点P为对称轴上一动点，当线段DE的长度最大时，求PD+PA的最小值；
（3）设点M为抛物线的顶点，在y轴上是否存在点Q，使∠AQM＝45°？若存在，求点Q的坐标；若不存在，请说明理由．







参考答案
1．（眉山中考 第26题 11分）如图1，在平面直角坐标系中，抛物线y＝﹣x2+bx+c经过点A（﹣5，0）和点B（1，0）.
（1）求抛物线的解析式及顶点D的坐标；
（2）点P是抛物线上A、D之间的一点，过点P作PE⊥x轴于点E，PG⊥y轴，交抛物线于点G.过点G作GF⊥x轴于点F.当矩形PEFG的周长最大时，求点P的横坐标；
B
A
C
O
D
E
F
G
P
y
x
图1
图2
A
B
C
D
y
x
M
N
O
（3）如图2，连接AD、BD，点M在线段AB上（不与A、B重合），作∠DMN＝∠DBA, MN交线段AD于点N，是否存在这样点M，使得△DMN为等腰三角形？若存在，求出AN的长；若不存在，请说明理由.





【解析】（1）抛物线的解析式为：y＝﹣(x+5）(x﹣1) ＝﹣x2﹣x+ ………………2分
配方得：y＝﹣（x+2）2+4 ，∴顶点D的坐标为（﹣2，4）. ………………………………3分
（2）设点P的坐标为（a，﹣a2﹣a+）,
则PE＝﹣a2﹣a+，PG＝2(﹣2﹣a)＝﹣4﹣2a. ………………………………4分
∴矩形PEFG的周长＝2(PE+PG)＝2(﹣a2﹣a+﹣4﹣2a)
＝﹣a2﹣a﹣
＝﹣(a+)2+ ……………………………6分
∵﹣＜0,
∴当a＝﹣时，矩形PEFG的周长最大，
此时，点P的横坐标为﹣.…………………… ………7分
（3）存在.∵AD＝BD， ∴∠DAB＝∠DBA.∵∠AMN+∠DMN＝∠MDB+∠DBA,
又∵∠DMN＝∠DBA, ∴∠AMN＝∠MDB,∴△AMN∽△BDM,
∴＝ ………………………………………………………8分
易求得：AB＝6，AD＝DB＝5. △DMN为等腰三角形有三种可能：
①当MN＝DM时，则△AMN≌△BDM,
∴AM＝BD＝5, ∴AN＝MB＝1; ………………………………………………………9分
②当DN＝MN时，则∠ADM＝∠DMN＝∠DBA,又∵∠DAM＝∠BAD, ∴△DAM∽△BAD,
∴AD2＝AM•BA.∴AM＝, BM＝6﹣＝,
∵＝ , ∴ ＝ ,
∴AN＝. ………………………………………………………………10分
③DN＝DM不成立.∵∠DNM＞∠DAB, 而∠DAB＝∠DMN，
∴∠DNM＞∠DMN，∴DN≠DM.
综上所述，存在点M满足要求，此时AN的长为1或.………………………………………11分

2.（绵阳中考 第24题）在平面直角坐标系中，将二次函数y=ax2（a＞0）的图象向右平移1个单位，再向下平移2个单位，得到如图所示的抛物线，该抛物线与x轴交于点A、B（点A在点B的左侧），OA=1，经过点A的一次函数y=kx+b（k≠0）的图象与y轴正半轴交于点C，且与抛物线的另一个交点为D，△ABD的面积为5．
（1）求抛物线和一次函数的解析式；
（2）抛物线上的动点E在一次函数的图象下方，求△ACE面积的最大值，并求出此时点E的坐标；
（3）若点P为x轴上任意一点，在（2）的结论下，求PE+PA的最小值．


【解析】（1）将二次函数y=ax2（a＞0）的图象向右平移1个单位，再向下平移2个单位，得到的抛物线解析式为y=a（x-1）2-2，∵OA=1，
∴点A的坐标为（-1，0），代入抛物线的解析式得，4a-2=0，∴，
∴抛物线的解析式为y=，即y=．令y=0，解得x1=-1，x2=3，
∴B（3，0），∴AB=OA+OB=4，∵△ABD的面积为5，∴=5，
∴yD=，代入抛物线解析式得，，解得x1=-2，x2=4，∴D（4，），
设直线AD的解析式为y=kx+b，∴，解得：，
∴直线AD的解析式为y=．
（2）过点E作EM∥y轴交AD于M，如图，设E（a，），则M（a，），

∴=，
∴S△ACE=S△AME-S△CME===，
=，
∴当a=时，△ACE的面积有最大值，最大值是，此时E点坐标为（）．
（3）作E关于x轴的对称点F，连接EF交x轴于点G，过点F作FH⊥AE于点H，交轴于点P，

∵E（），OA=1，∴AG=1+=，EG=，∴，
∵∠AGE=∠AHP=90°∴sin，∴，∵E、F关于x轴对称，
∴PE=PF，∴PE+AP=FP+HP=FH，此时FH最小，∵EF=，∠AEG=∠HEF，
∴=，∴．∴PE+PA的最小值是3．
3.（攀枝花中考 第24题 ）在平面直角坐标系xOy中，已知A（0，2），动点P在y=x的图象上运动（不与O重合），连接AP．过点P作PQ⊥AP，交x轴于点Q，连接AQ．
（1）求线段AP长度的取值范围；
（2）试问：点P运动的过程中，∠QAP是否为定值？如果是，求出该值；如果不是，请说明理由．
（3）当△OPQ为等腰三角形时，求点Q的坐标．
【解析】（1）由y=x知：∠POQ=30°，
当AP⊥OP时，AP取得最小值=OA•sin∠AOP=2sin60°=；
（2）过点P作PH⊥x轴于点H、交过点A平行于x轴的直线与点G，

∴∠APQ=90°，∴∠AGP+∠APG=90°，∠APG+∠QPH=90°，
∴∠QPH=∠PAG，∴△PAG∽△QPH，∴tan∠PAQ====，
则∠QAP=30°；
（3） 设：OQ=m，则AQ2=m2+4=4PQ2，①当OQ=PQ时，
即PQ=OQ=m，则m2+4=4m2，解得：m=；
②当PO=OQ时，同理可得：m=±（4+4）；
③当PQ=OP时，同理可得：m=；
故点Q的坐标为（，0）或（-，0）或（4+4，0）或（-4-4，0）或（2，0）或（-2，0）．

6. 已知抛物线y=-x2+bx+c的对称轴为直线x=1，其图象与x轴相交于A，B两点，与y轴相交于点C（0，3）．
（1）求b，c的值；（2）直线1与x轴相交于点P．
①如图1，若l∥y轴，且与线段AC及抛物线分别相交于点E，F，点C关于直线x=1的对称点为点D，求四边形CEDF面积的最大值；
②如图2，若直线1与线段BC相交于点Q，当△PCQ∽△CAP时，求直线1的表达式．


【解析】（1）由题意得：，∴b=2，c=3，
（2）①如图1，∵点C关于直线x=1的对称点为点D，
∴CD∥OA，∴3=-x2+2x+3，解得：x1=0，x2=2，∴D（2，3），
∵抛物线的解析式为y=-x2+2x+3，∴令y=0，解得x1=-1，x2=3，∴B（-1，0），A（3，0），
设直线AC的解析式为y=kx+b，
∴，解得：，∴直线AC的解析式为y=-x+3，设F（a，-a2+2a+3），E（a，-a+3），
∴EF=-a2+2a+3+a-3=-a2+3a，
四边形CEDF的面积=S△EFC+S△EFD===-a2+3a=，
∴当a=时，四边形CEDF的面积有最大值，最大值为．
②当△PCQ∽△CAP时，∴∠PCA=∠CPQ，∠PAC=∠PCQ，∴PQ∥AC，
∵C（0，3），A（3，0），∴OA=OC，
∴∠OCA=∠OAC=∠PCQ=45°，
∴∠BCO=∠PCA，如图2，过点P作PM⊥AC交AC于点M，
∴，设PM=b，则CM=3b，AM=b，
∵，∴，∴，
∴，∴，∴，
设直线l的解析式为y=-x+n，∴，∴．
∴直线l的解析式为y=-x+．

5.（绵阳中考25题）如图，在以点O为中心的正方形ABCD中，AD=4，连接AC，动点E从点O出发沿O→C以每秒1个单位长度的速度匀速运动，到达点C停止．在运动过程中，△ADE的外接圆交AB于点F，连接DF交AC于点G，连接EF，将△EFG沿EF翻折，得到△EFH．
（1）求证：△DEF是等腰直角三角形；
（2）当点H恰好落在线段BC上时，求EH的长；
（3）设点E运动的时间为t秒，△EFG的面积为S，求S关于时间t的关系式．



【解析】（1）证明：∵四边形ABCD是正方形，
∴∠DAC=∠CAB=45°，
∴∠FDE=∠CAB，∠DFE=∠DAC，
∴∠FDE=∠DFE=45°，∴∠DEF=90°，∴△DEF是等腰直角三角形；
（2）设OE=t，连接OD，∴∠DOE=∠DAF=90°，∵∠OED=∠DFA，∴△DOE∽△DAF，
∴，∴t，
又∵∠AEF=∠ADG，∠EAF=∠DAG，
∴△AEF∽△ADG，∴，∴，又∵AE=OA+OE=2+t，
∴，∴EG=AE-AG=，
当点H恰好落在线段BC上∠DFH=∠DFE+∠HFE=45°+45°=90°，∴△ADF∽△BFH，
∴，∵AF∥CD，∴，∴，∴，
解得：t1=，t2=（舍去），∴EG=EH=；
（3）过点F作FK⊥AC于点K，由（2）得EG=，∵DE=EF，∠DEF=90°，
∴∠DEO=∠EFK，∴△DOE≌△EKF（AAS），∴FK=OE=t，∴S=．

6．（资阳中考 第24题）如图，在平面直角坐标系xOy中，已知抛物线y＝ax2﹣2x+c与直线y＝kx+b都经过A（0，﹣3）、B（3，0）两点，该抛物线的顶点为C．
（1）求此抛物线和直线AB的解析式；
（2）设直线AB与该抛物线的对称轴交于点E，在射线EB上是否存在一点M，过M作x轴的垂线交抛物线于点N，使点M、N、C、E是平行四边形的四个顶点？若存在，求点M的坐标；若不存在，请说明理由；
（3）设点P是直线AB下方抛物线上的一动点，当△PAB面积最大时，求点P的坐标，并求△PAB面积的最大值．

【解析】（1）∵抛物线y＝ax2﹣2x+c经过A（0，﹣3）、B（3，0）两点，
∴，
∴，
∴抛物线的解析式为y＝x2﹣2x﹣3，
∵直线y＝kx+b经过A（0，﹣3）、B（3，0）两点，
∴，解得：，
∴直线AB的解析式为y＝x﹣3，
（2）∵y＝x2﹣2x﹣3＝（x﹣1）2﹣4，
∴抛物线的顶点C的坐标为（1，﹣4），
∵CE∥y轴，
∴E（1，﹣2），
∴CE＝2，
①如图，若点M在x轴下方，四边形CEMN为平行四边形，则CE＝MN，
设M（a，a﹣3），则N（a，a2﹣2a﹣3），
∴MN＝a﹣3﹣（a2﹣2a﹣3）＝﹣a2+3a，
∴﹣a2+3a＝2，
解得：a＝2，a＝1（舍去），
∴M（2，﹣1），
②如图，若点M在x轴上方，四边形CENM为平行四边形，则CE＝MN，
设M（a，a﹣3），则N（a，a2﹣2a﹣3），
∴MN＝a2﹣2a﹣3﹣（a﹣3）＝a2﹣3a，
∴a2﹣3a＝2，
解得：a＝，a＝（舍去），
∴M（，），
综合可得M点的坐标为（2，﹣1）或（）．
（3）如图，作PG∥y轴交直线AB于点G，
设P（m，m2﹣2m﹣3），则G（m，m﹣3），
∴PG＝m﹣3﹣（m2﹣2m﹣3）＝﹣m2+3m，
∴S△PAB＝S△PGA+S△PGB＝＝＝﹣，
∴当m＝时，△PAB面积的最大值是，此时P点坐标为（）．
8. 在矩形ABCD中，连结AC，点E从点B出发，以每秒1个单位的速度沿着B→A→C的路径运动，运动时间为t（秒）．过点E作EF⊥BC于点F，在矩形ABCD的内部作正方形EFGH．
（1）如图，当AB＝BC＝8时，
①若点H在△ABC的内部，连结AH、CH，求证：AH＝CH；
②当0＜t≤8时，设正方形EFGH与△ABC的重叠部分面积为S，求S与t的函数关系式；
（2）当AB＝6，BC＝8时，若直线AH将矩形ABCD的面积分成1：3两部分，求t的值．

【解答】解：（1）①如图1中，

∵四边形EFGH是正方形，AB＝BC，∴BE＝BG，AE＝CG，∠BHE＝∠BGH＝90°，
∴∠AEH＝∠CGH＝90°，∵EH＝HG，∴△AEH≌△CGH（SAS），∴AH＝CH．
②如图1中，当0＜t≤4时，重叠部分是正方形EFGH，S＝t2．
如图2中，当4＜t≤8时，重叠部分是五边形EFGMN，S＝S△ABC﹣S△AEN﹣S△CGM＝×8×8﹣2×（8﹣t）2＝﹣t2+32t﹣32．

综上所述，S＝．
（2）如图3﹣1中，延长AH交BC于M，当BM＝CM＝4时，直线AH将矩形ABCD的面积分成1：3两部分．

∵EH∥BM，∴＝，∴＝，∴t＝．
如图3﹣2中，延长AH交CD于M交BC的延长线于K，当CM＝DM＝3时，直线AH将矩形ABCD的面积分成1：3两部分，易证AD＝CK＝8，

∵EH∥BK，∴＝，∴＝，∴t＝．
如图3﹣3中，当点E在线段AC上时，延长AH交CD于M，交BC的延长线于N．当CM＝DM时，直线AH将矩形ABCD的面积分成1：3两部分，易证AD＝CN＝8．

在Rt△ABC中，AC＝＝10，∵EF∥AB，∴＝，
∴＝，∴EF＝（16﹣t），∵EH∥CN，∴＝，
∴＝，解得t＝．
综上所述，满足条件的t的值为s或s或s．
8.（金华中考 第24题 ）如图，在等腰Rt△ABC中，∠ACB=90°，AB=.点D，E分别在边AB，BC上，将线段ED绕点E按逆时针方向旋转90°得到EF.
（1）如图1，若AD=BD，点E与点C重合，AF与DC相交于点O,求证：BD=2DO.
（2）已知点G为AF的中点.
①如图2，若AD=BD，CE=2，求DG的长.
②若AD=6BD,是否存在点E,使得△DEG是直角三角形？若存在，求CE的长；若不存在，试说明理由.
图1 图2 图3
D
A
(E)
B
C
F
F
G
D
A
E
B
C
F
G
D
A
E
B
C
(第24题)
O





【解析】（1）由旋转性质得：CD=CF，∠DCF=90°.
∵△ABC是等腰直角三角形，AD=BD.
∴∠ADO=90°，CD=BD=AD,
∴∠DCF=∠ADC.
在△ADO和△FCO中，

∴△ADO≌△FCO.
∴DO=CO.
∴BD=CD=2OD.
（2）①如图1,分别过点D,F作DN⊥BC于点N,FM⊥BC于点M,连结BF.
G
F
D
C
A
B
E
N
M
图1
∴∠DNE=∠EMF=90°.
又∵∠NDE=∠MEF,DE=EF,
∴△DNE≌△EMF, ∴DN=EM.
又∵BD=,∠ABC=45°,∴DN=EM=7,
∴BM=BC－ME－EC=5,∴MF=NE= NC－EC=5.
∴BF=.
∵点D,G分别是AB,AF的中点,
∴DG=BF=.
②过点D作DH⊥BC于点H.
∵AD=6BD，AB=，∴BD=.
ⅰ）当∠DEG=90°时，有如图2，3两种情况，设CE=t.
∵∠DEF=90°，∠DEG=90°，
∴点E在线段AF上.
∴BH=DH=2,BE=14－t，HE=BE－BH=12－t.
∵△DHE∽△ECA，∴，即，解得.
∴或.

图2 图3 图4
F
G
D
A
E
B
C
H
F
G
D
A
E
B
C
H
F
G
D
A
E
B
C
H
N
M
K






ⅱ） 当DG∥BC时，如图4.
过点F作FK⊥BC于点K,延长DG交AC于点N，延长AC并截取MN=NA.连结
FM.
则NC=DH=2,MC=10.
设GN=t,则FM=2t,BK=14－2t.
∵△DHE≌△EKF， ∴KE=DH=2,KF=HE=14－2t,
∵MC=FK, ∴14－2t=10, 得t=2.
∵GN=EC=2, GN∥EC，
∴四边形GECN是平行四边形.
而∠ACB=90°，
∴四边形GECN是矩形，∴∠EGN=90°.
∴当EC=2时，有∠DGE=90°.
ⅲ）当∠EDG=90°时，如图5.
F
G
D
A
E
B
C
H
N
M
K
P
图5
过点G，F分别作AC的垂线，交射线AC于点N, M，过点E作EK⊥FM于点K，过点D作GN的垂线，交NG的延长线于点P.则PN=HC=BC-HB=12,
设GN=t，则FM=2t，∴PG=PN-GN=12-t.
由△DHE≌△EKF可得：FK=2，
∴CE=KM=2t-2，
∴HE=HC-CE=12-(2t-2)=14-2t，
∴EK=HE=14-2t,
AM=AC+CM=AC+EK=14+14-2t=28-2t，
∴MN=AM=14-t，NC=MN-CM=t，
∴PD=t-2，
由△GPD∽△DHE可得：，即，
解得，（舍去）.
∴CE=2t-2=.
所以，CE的长为：,,2或.

9．（资阳中考 第24题13分）如图，抛物线y＝﹣x2+bx+c过点A（3，2），且与直线y＝﹣x+交于B、C两点，点B的坐标为（4，m）．

（1）求抛物线的解析式；
（2）点D为抛物线上位于直线BC上方的一点，过点D作DE⊥x轴交直线BC于点E，点P为对称轴上一动点，当线段DE的长度最大时，求PD+PA的最小值；
（3）设点M为抛物线的顶点，在y轴上是否存在点Q，使∠AQM＝45°？若存在，求点Q的坐标；若不存在，请说明理由．
【解答】解：（1）将点B的坐标为（4，m）代入y＝﹣x+，
m＝﹣4+＝﹣，∴B的坐标为（4，﹣），将A（3，2），B（4，﹣）代入y＝﹣x2+bx+c，
解得b＝1，c＝，∴抛物线的解析式y＝；
（2）设D（m，），则E（m，﹣m+），
DE＝（）﹣（﹣m+）＝＝﹣（m﹣2）2+2，
∴当m＝2时，DE有最大值为2，此时D（2，），
作点A关于对称轴的对称点A'，连接A'D，与对称轴交于点P．

PD+PA＝PD+PA'＝A'D，此时PD+PA最小，
∵A（3，2），∴A'（﹣1，2），A'D＝＝，
即PD+PA的最小值为；
（3）作AH⊥y轴于点H，连接AM、AQ、MQ、HA、HQ，

∵抛物线的解析式y＝，∴M（1，4），∵A（3，2），∴AH＝MH＝2，H（1，2）
∵∠AQM＝45°，∠AHM＝90°，∴∠AQM＝∠AHM，
可知△AQM外接圆的圆心为H，

∴QH＝HA＝HM＝2设Q（0，t），则＝2，
t＝2+或2﹣
∴符合题意的点Q的坐标：Q1（0，2﹣）、Q2（0，2）．