2021_2023年高考数学真题分类汇编专题05立体几何填空题文

专题05 立体几何（填空题）（文）

近三年高考真题

知识点1：三视图

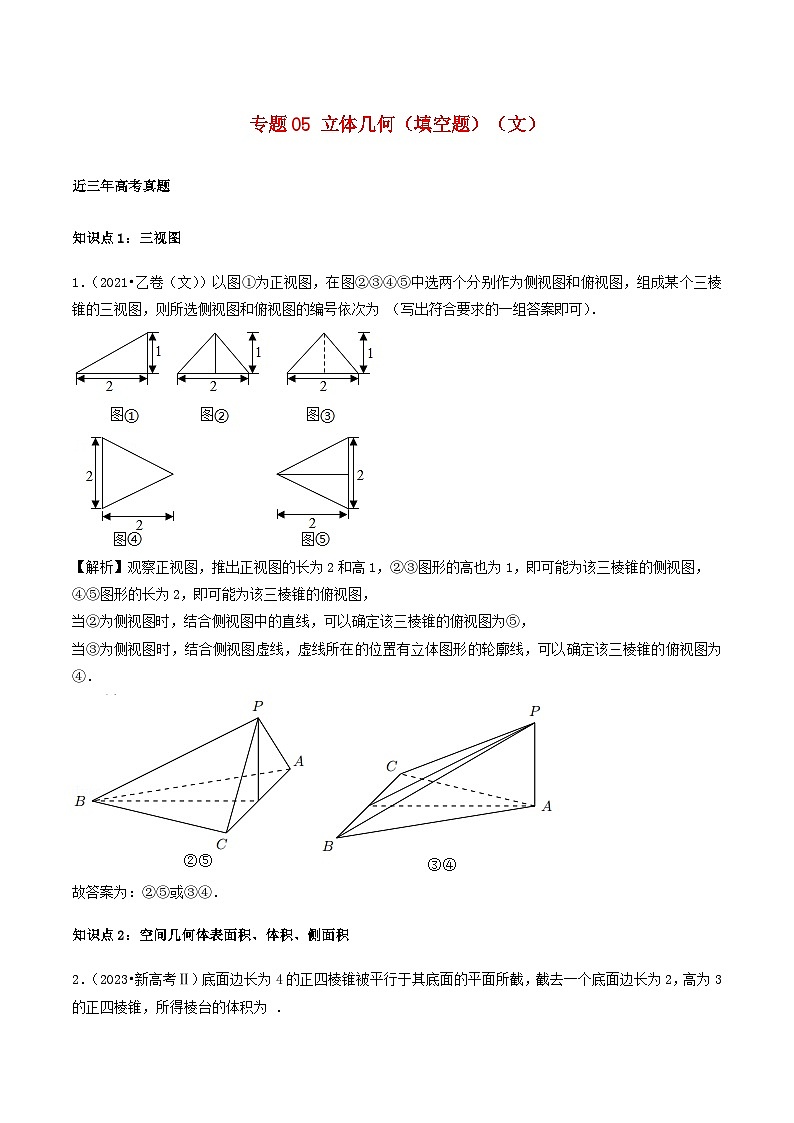
1．（2021•乙卷（文））以图①为正视图，在图②③④⑤中选两个分别作为侧视图和俯视图，组成某个三棱锥的三视图，则所选侧视图和俯视图的编号依次为 （写出符合要求的一组答案即可）．

【解析】观察正视图，推出正视图的长为2和高1，②③图形的高也为1，即可能为该三棱锥的侧视图，

④⑤图形的长为2，即可能为该三棱锥的俯视图，

当②为侧视图时，结合侧视图中的直线，可以确定该三棱锥的俯视图为⑤，

当③为侧视图时，结合侧视图虚线，虚线所在的位置有立体图形的轮廓线，可以确定该三棱锥的俯视图为④．

故答案为：②⑤或③④．

知识点2：空间几何体表面积、体积、侧面积

2．（2023•新高考Ⅱ）底面边长为4的正四棱锥被平行于其底面的平面所截，截去一个底面边长为2，高为3的正四棱锥，所得棱台的体积为 ．

【解析】如图所示，根据题意易知△，

，又，

，，又上下底面正方形边长分别为2，4，

所得棱台的体积为．

故答案为：28．

3．（2023•新高考Ⅰ）在正四棱台中，，，，则该棱台的体积为 ．

【解析】如图，设正四棱台的上下底面中心分别为，，

过作，垂足点为，由题意易知，又，

，又，，

该四棱台的体积为．

故答案为：．

4．（2021•上海）已知圆柱的底面半径为1，高为2，则圆柱的侧面积为．

【答案】．

【解析】圆柱的底面半径为，高为，

所以圆柱的侧面积为．

故答案为：．

知识点3：球相关问题

5．（2023•甲卷（文））在正方体中，，为的中点，若该正方体的棱与球的球面有公共点，则球的半径的取值范围是 ．

【答案】，．

【解析】设球的半径为，

当球是正方体的外接球时，恰好经过正方体的每个顶点，所求的球的半径最大，

若半径变得更大，球会包含正方体，导致球面和棱没有交点，

正方体的外接球直径为体对角线长，

即，，故，

分别取侧枝，，，的中点，，，，

则四边形是边长为4的正方形，且为正方形的对角线交点，

连接，则，

当球的一个大圆恰好是四边形的外接圆，球的半径最小，

即的最小值为，

综上，球的半径的取值范围是，．

故答案为：，．

6．（2023•乙卷（文））已知点，，，均在半径为2的球面上，是边长为3的等边三角形，平面，则．

【答案】2．

【解析】设的外接圆圆心为，半径为，

则，解得，

设三棱锥的外接球球心为，连接，，

则，，

，，解得．