2023重庆市长寿中学校高二下学期期中数学试题含解析

重庆市长寿中学校2024届高二下·半期考试

数学试题

一、单项选择题（本大题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的）

1. 设数列的前项和，则的值为（    ）

A. 8 B. 9 C. 10 D. 11

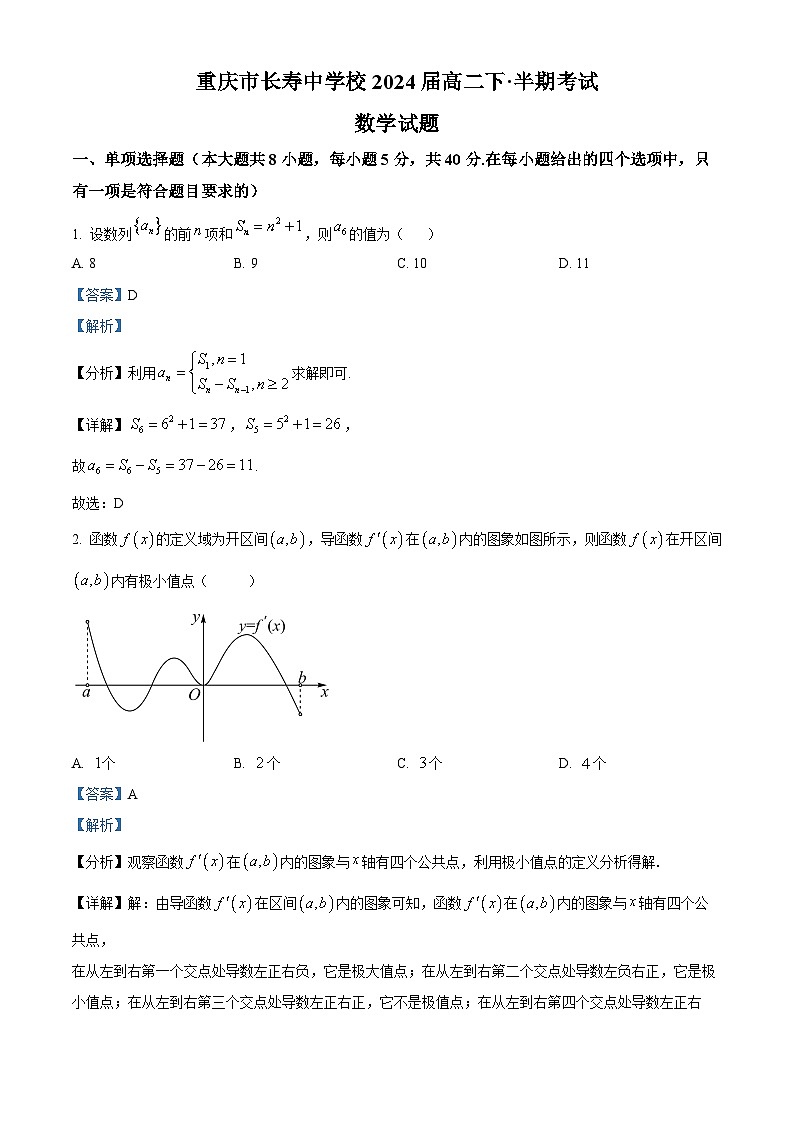
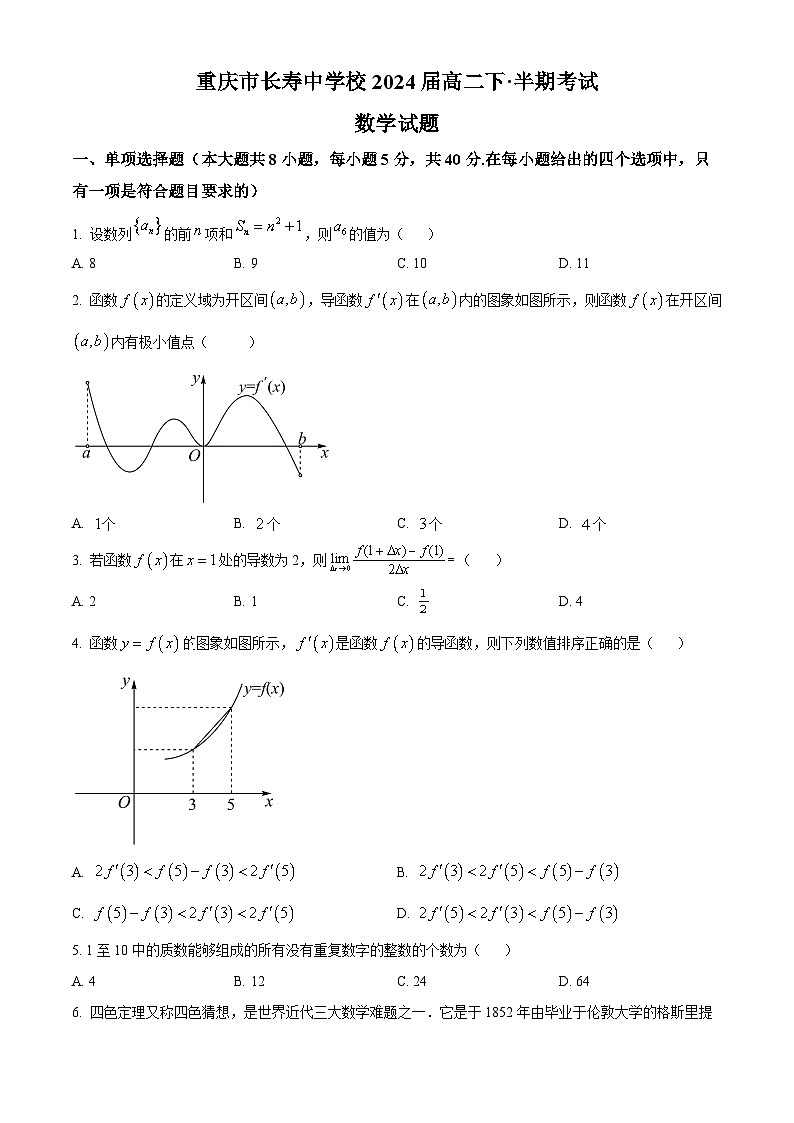
2. 函数的定义域为开区间，导函数在内的图象如图所示，则函数在开区间内有极小值点（       ）

A. 个 B. 个 C. 个 D. 个

3. 若函数在处的导数为2，则（    ）

A. 2 B. 1 C.  D. 4

4. 函数图象如图所示，是函数的导函数，则下列数值排序正确的是（    ）

A.  B.

C.  D.

5. 1至10中的质数能够组成的所有没有重复数字的整数的个数为（    ）

A. 4 B. 12 C. 24 D. 64

6. 四色定理又称四色猜想，是世界近代三大数学难题之一．它是于1852年由毕业于伦敦大学的格斯里提出来的，其内容是“任何一张地图只用四种颜色就能使具有共同边界的国家着上不同的颜色”．某校数学兴趣小组在研究给四棱锥的各个面涂颜色时，提出如下的“四色问题”：要求相邻面（含公共棱的面）不得使用同一颜色，现有4种颜色可供选择，则不同的涂法有（    ）

A. 36种 B. 72种 C. 48种 D. 24种

7. 已知函数，则“”是“函数在上单调递减”的（    ）

A. 充分不必要条件 B. 必要不充分条件 C. 充要条件 D. 既不充分也不必要条件

8. 已知定义在上的函数的导函数为，且满足，则关于不等式的解集为（    ）

A.  B.  C.  D.

二、多项选择题（本大题共4个小题，每小题5分，共20分.在每小题给出的四个选项中，有多项是符合题目要求的.全部选对得5分，部分选对得2分，有选错的得0分）

9. 下列各式的运算结果中，等于的有（    ）

A.  B.

C.  D.

10. 对于定义在上的可导函数，为其导函数，下列说法不正确的是（    ）

A. 使的x一定是函数的极值点

B. 在上单调递增是在上恒成立充要条件

C. 函数切线与函数可以有两个公共点

D. 若函数既有极小值又有极大值，则其极小值一定不会比它的极大值大

11. 已知函数，则（    ）

A. 当时，函数的极大值为 B. 若函数在上单调递增，则或

C. 函数必有两个极值点 D. 函数必有三个零点

12. 设函数（），则（    ）

A. 当时，存在唯一极值点

B. 当时，

C. 当时，在上单调递增

D. 当时，存在唯一实数使得函数恰有两个零点

三、填空题（本大题共4小题，每小题5分，共20分）

13. 数列中，若，且，则__________.

14. 的值为________．

15. 曲线在处切线的倾斜角是______.

16. 已知，，直线与曲线相切，则最小值是______.

四、解答题（本大题共6小题，共70分.解答应写出文字说明，证明过程或演算步骤）

17. 从0-9这10个数字取出3个数字，试问：

（1）有多少个没有重复数字的排列方法？

（2）能组成多少个没有重复数字的三位数？

（3）能组成多少个没有重复数字的三位数奇数？

（注：要有适当的文字说明，最终结果用数字表示）

18. 已知函数.

（1）设为偶函数，当时，，求曲线在点处的切线方程；

（2）设，求函数的极值.

19. 已知函数在处有极值10.

（Ⅰ）求；

（Ⅱ）求在上的最小值.

20. 某学校高二年级一个学习兴趣小组进行社会实践活动，决定对某“著名品牌”系列进行市场销售量调研，通过对该品牌的系列一个阶段的调研得知，发现系列每日的销售量（单位：千克）与销售价格（元/千克）近似满足关系式，其中，为常数.已知销售价格为6元/千克时，每日可售出系列15千克.

（1）求函数的解析式；

（2）若系列的成本为4元/千克，试确定销售价格的值，使该商场每日销售系列所获得的利润最大.

21. 已知函数，，其中为常数.

（1）当时，试判断单调性；

（2）若在其定义域内为增函数，求实数a的取值范围；

（3）设函数，当时，若存在，对任意的，总有成立，求实数m的取值范围.

22. 已知函数,其中．

（1）当时,求曲线在点处的切线方程;

（2）当时,判断的零点个数,并加以证明;

（3）当时,证明:存在实数m,使恒成立．