模型38 梅涅劳斯定理、塞瓦定理（讲+练）-备战2023年中考数学解题大招复习讲义（全国通用）

这是一份模型38 梅涅劳斯定理、塞瓦定理（讲+练）-备战2023年中考数学解题大招复习讲义（全国通用），文件包含模型38梅涅劳斯定理塞瓦定理原卷版docx、模型38梅涅劳斯定理塞瓦定理解析版docx等2份试卷配套教学资源，其中试卷共46页， 欢迎下载使用。
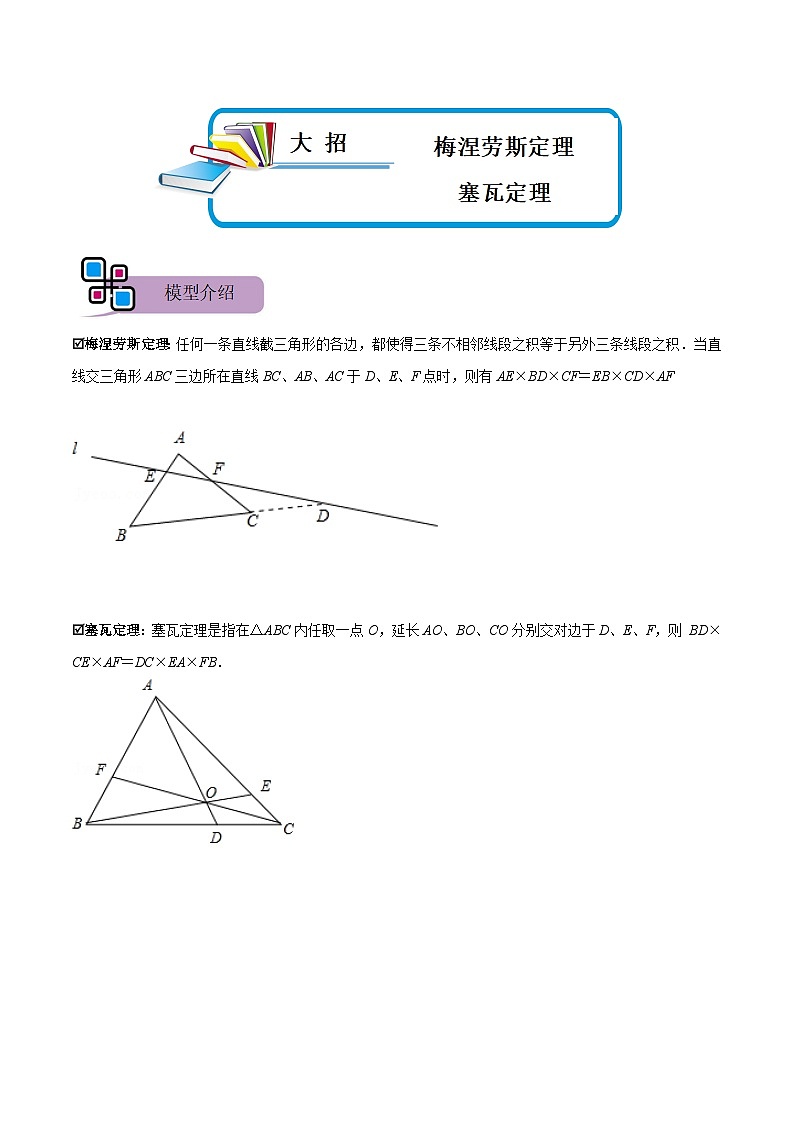
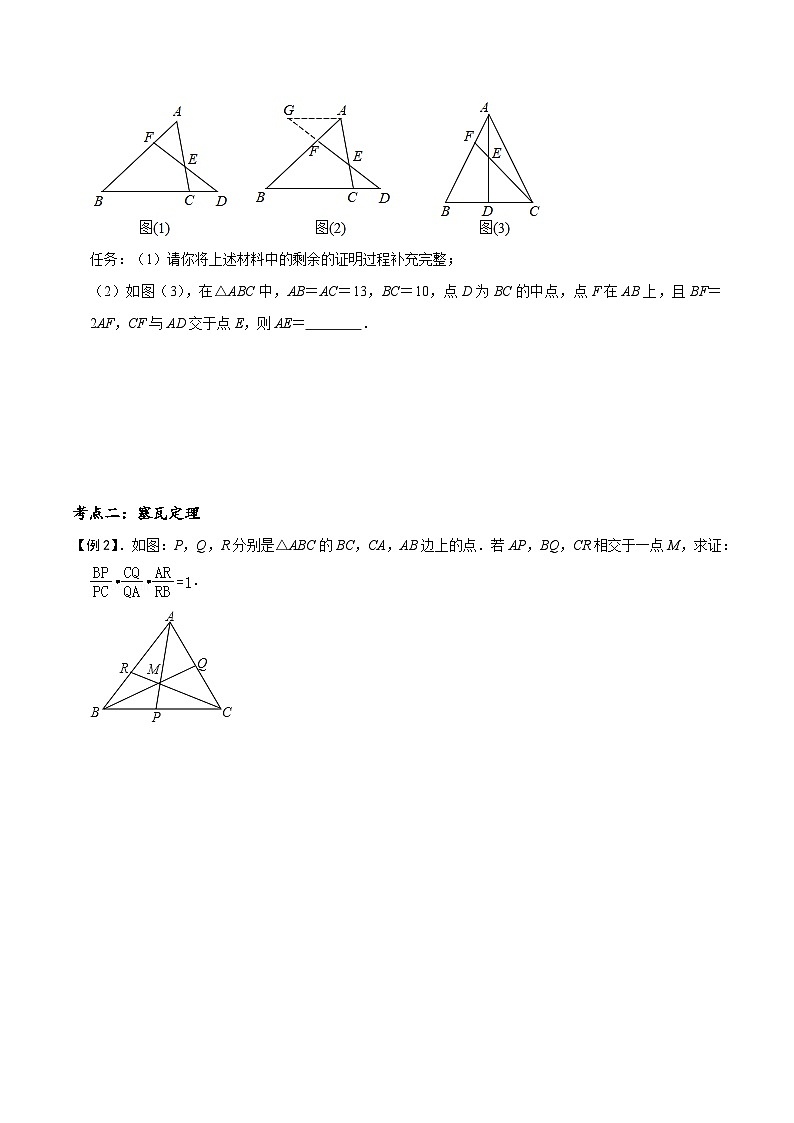
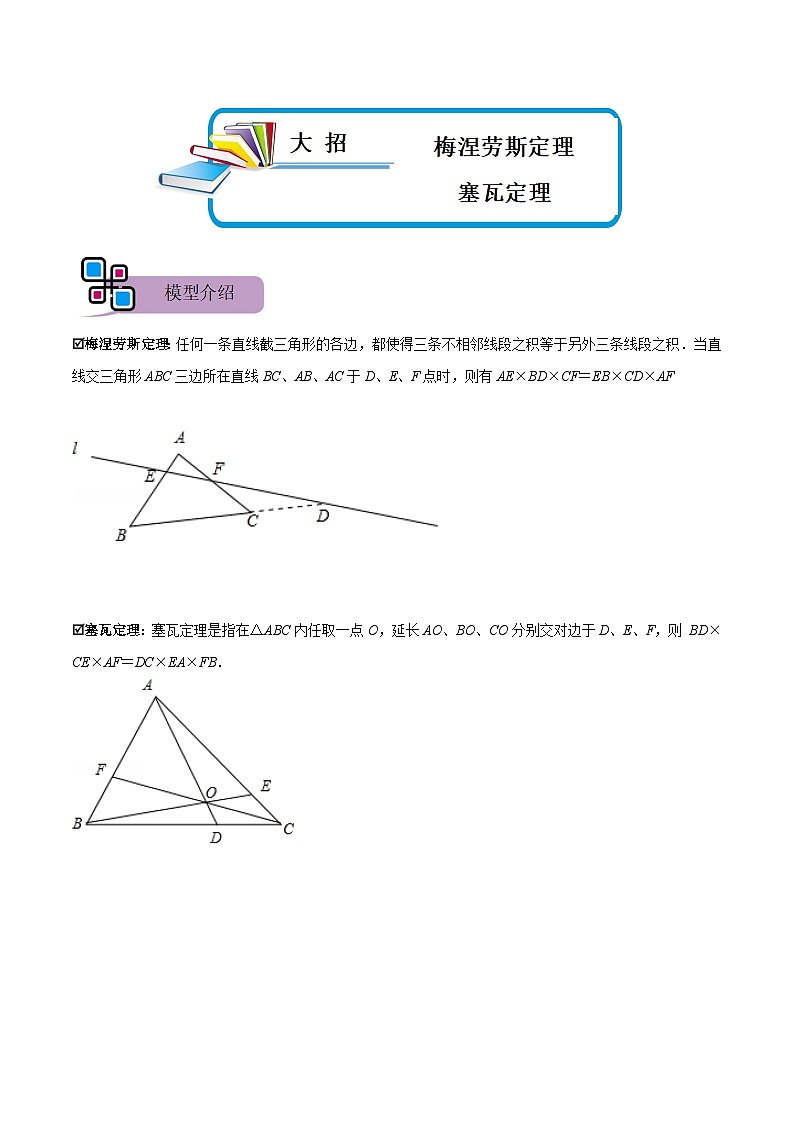
           梅涅劳斯定理：任何一条直线截三角形的各边，都使得三条不相邻线段之积等于另外三条线段之积．当直线交三角形ABC三边所在直线BC、AB、AC于D、E、F点时，则有AE×BD×CF＝EB×CD×AF   塞瓦定理：塞瓦定理是指在△ABC内任取一点O，延长AO、BO、CO分别交对边于D、E、F，则 BD×CE×AF＝DC×EA×FB．声        考点一：梅涅劳斯定理【例1】．如图，等边△ABC的边长为2，F为AB中点，延长BC至D，使CD＝BC，连接FD交AC于E，则四边形BCEF的面积为　　     ．  变式训练【变式1-1】．如图，D、E、F内分正△ABC的三边AB、BC、AC均为1：2两部分，AD、BE、CF相交成的△PQR的面积是△ABC的面积的（　　）A． B． C． D．  【变式1-2】．梅涅劳斯定理梅涅劳斯（Menelaus）是古希腊数学家，他首先证明了梅涅劳斯定理，定理的内容是：如图（1），如果一条直线与△ABC的三边AB，BC，CA或它们的延长线交于F、D、E三点，那么一定有••＝1．下面是利用相似三角形的有关知识证明该定理的部分过程：证明：如图（2），过点A作AG∥BC，交DF的延长线于点G，则有＝．任务：（1）请你将上述材料中的剩余的证明过程补充完整；（2）如图（3），在△ABC中，AB＝AC＝13，BC＝10，点D为BC的中点，点F在AB上，且BF＝2AF，CF与AD交于点E，则AE＝　    　．     考点二：塞瓦定理【例2】．如图：P，Q，R分别是△ABC的BC，CA，AB边上的点．若AP，BQ，CR相交于一点M，求证：．         变式训练【变式2-1】．请阅读下列材料，并完成相应任务如图，塞瓦定理是指在△ABC内任取一点O，延长AO，BO，CO分别交对边D，E，F于，则××＝1．任务：（1）当点D，E分别为边BC，AC的中点时，求证：点F为AB的中点；（2）若△ABC为等边三角形，AB＝12，AE＝4，点D是BC边的中点，求BF的长．【变式2-2】．请阅读下列材料，并完成相应任务 塞瓦定理定理内容：如图1，塞瓦定理是指在△ABC内任取一点O，延长AO，BO，CO分别交对边于D，E，F，则．数学意义：使用塞瓦定理可以进行直线形中线段长度比例的计算，其逆定理还可以用来进行三点共线、三线共点等问题的判定方法，是平面几何学以及射影几何学中的一项基本定理，具有重要的作用． 任务解决：（1）如图2，当点D，E分别为边BC，AC的中点时，求证：点F为AB的中点；（2）若△ABC为等边三角形（如图3），AB＝12，AE＝4，点D是BC边的中点，求BF的长，并直接写出△BOF的面积．                    1．如图，在△ABC中，M是AC的中点，E是AB上一点，AE＝AB，连接EM并延长，交BC的延长线于D，则＝（　　）A． B．2 C． D．   2．如图，在△ABC中，D、E分别是BC、AC上的点，AD与BE相交于点G，若AG：GD＝4：1，BD：DC＝2：3，则AE：EC的值是（　　）A． B． C． D．    3．如图，在△ABC中，AD是BC边上的中线，F是AD边上一点．射线CF交AB于点E，且，则等于　   　．  4．如图，在△ABC中，点D是AB边上的一点，且AD＝3BD，连接CD并取CD的中点E，连接BE，若∠ACD＝∠BED＝45°，且CD＝6，则AB的长为 　     　．  5．如图，在△ABC中，∠ACB＝90°，AC＝8，BC＝16，AD是边BC的中线，过点C作CE⊥AD于点E，连接BE并延长交AC于点F，则AD的长是 　   　，EF的长是 　　    ．  6．如图，△ABC中，D、E是BC边上的点，BD：DE：EC＝3：2：1，M在AC边上，CM：MA＝1：2，BM交AD、AE于H、G，则BH：HG：GM等于　    　．7．如图，▱ABCD的对角线相交于点O，在AB的延长线上任取一点E，连接OE交BC于点F．若AB＝a，AD＝c，BE＝b，则BF＝　      　．  8．在△ABC中，∠ACB＝90°，AC＝BC，AM为BC边上的中线，CD⊥AM于点D，CD的延长线交于点，求的值．    9．如图，在△ABC中，M是AC的中点，E、F是BC上的两点，且BE＝EF＝FC，求BN：NQ：QM的值．       10．如图，△ABC中，∠ACB＝90°，CD⊥AB于点D，E为BC上一点，AE交CD于点F，EH⊥AB于点H，若CF＝2FD，EH＝，求CE•BE的值．     11．如图，△ABC中，AD⊥BC于点D，E是AB上一点，连接DE，2∠C+∠BDE＝180°．（1）求证：∠BDE＝2∠CAD；（2）若AC＝BD，∠AED＝∠ACB，求证BE＝2CD；（3）若AE＝kBE，BD＝mCD，则的值为 　．　（用含m，k的式子表示）．       12．如图1，Rt△ABC中，∠BAC＝90°，AD是中线，BE⊥AD，垂足为E，点F在AD上，∠ACF＝∠DBE．（1）求证：∠ABD＝∠CFD；（2）探究线段AF，DE的数量关系，并证明你的结论；（3）如图2，延长BE交CF于点P，AB＝AF，求的值．                    13．如图1，△ABC中，AB＝AC，点D在BA的延长线上，点E在BC上，DE＝DC，点F是DE与AC的交点，且DF＝FE．  （1）图1中是否存在与∠BDE相等的角？若存在，请找出，并加以证明，若不存在，说明理由；  （2）求证：BE＝EC；  （3）若将“点D在BA的延长线上，点E在BC上”和“点F是DE与AC的交点，且DF＝FE”分别改为“点D在AB上，点E在CB的延长线上”和“点F是ED的延长线与AC的交点，且DF＝kFE”，其他条件不变（如图2）．当AB＝1，∠ABC＝a时，求BE的长（用含k、a的式子表示）．                 14．阅读以下材料，并按要求完成相应的任务．塞瓦（GiovanniCeva，1648～1734）意大利水利工程师，数学家，塞瓦定理载于1678年发表的《直线论》一书，塞瓦定理是指如图1，在△ABC内任取一点O，延长AO，BO，CO分别交对边于D，F，E，则．下面是该定理的部分证明过程：如图2，过点A作BC的平行线分别交BE，CF的延长线于点M，N．则∠N＝∠FCB，∠NAF＝∠FBC．∴△NAF∽△CBF．∴①．同理可得△NOA∽△COD．∴②．任务一：（1）请分别写出与△MOA，△MEA相似的三角形；（2）写出由（1）得到的比例线段；任务二：结合①②和（2），完成该定理的证明；任务三：如图3，△ABC中，∠ACB＝90°，AC＝4，BC＝3，CD⊥AB，垂足为D，点E为DC的中点，连接AE并延长，交BC于点F，连接BE并延长，交AC于点G．小明同学自学了上面定理之后解决了如图3所示的问题，并且他用所学知识已经求出了BF与FC的比是25：16，请你直接写出△ECG与△EAG面积的比．     15．问题提出如图（1），在△ABC中，AB＝AC，D是AC的中点，延长BC至点E，使DE＝DB，延长ED交AB于点F，探究的值．问题探究（1）先将问题特殊化．如图（2），当∠BAC＝60°时，直接写出的值；（2）再探究一般情形．如图（1），证明（1）中的结论仍然成立．问题拓展如图（3），在△ABC中，AB＝AC，D是AC的中点，G是边BC上一点，＝（n＜2），延长BC至点E，使DE＝DG，延长ED交AB于点F．直接写出的值（用含n的式子表示）．            16．阅读下面材料，完成（1）﹣（3）题数学课上，老师出示了这样一道题：如图1，△ABC中，∠BAC＝90°，点D、E在BC上，AD＝AB，AB＝kBD（其中＜k＜1）∠ABC＝∠ACB+∠BAE，∠EAC的平分线与BC相交于点F，BG⊥AF，垂足为G，探究线段BG与AC的数量关系，并证明．同学们经过思考后，交流了自己的想法：小明：“通过观察和度量，发现∠BAE与∠DAC相等．”小伟：“通过构造全等三角形，经过进一步推理，可以得到线段BG与AC的数量关系．”……老师：“保留原题条件，延长图1中的BG，与AC相交于点H（如图2），可以求出的值．”（1）求证：∠BAE＝∠DAC；（2）探究线段BG与AC的数量关系（用含k的代数式表示），并证明；（3）直接写出的值（用含k的代数式表示）．