


2022-2023学年山西省吕梁柳林县联考七下数学期末学业水平测试试题含答案
展开2022-2023学年山西省吕梁柳林县联考七下数学期末学业水平测试试题
(时间:120分钟 分数:120分)
学校_______ 年级_______ 姓名_______
注意事项
1.考生要认真填写考场号和座位序号。
2.试题所有答案必须填涂或书写在答题卡上,在试卷上作答无效。第一部分必须用2B 铅笔作答;第二部分必须用黑色字迹的签字笔作答。
3.考试结束后,考生须将试卷和答题卡放在桌面上,待监考员收回。
一、选择题(每小题3分,共30分)
1.下列四个多项式中,不能因式分解的是( )
A.a2+a B.![]() C.
C.![]() D.
D.![]()
2.张浩调查统计了他们家5月份每次打电话的通话时长,并将统计结果进行分组(每组含量最小值,不含最大值),将分组后的结果绘制成如图所示的频数分布直方图,则下列说法中不正确的是( )
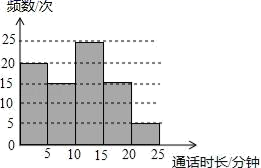
A.张浩家5月份打电话的总频数为80次
B.张浩家5月份每次打电话的通话时长在5﹣10分钟的频数为15次
C.张浩家5月份每次打电话的通话时长在10﹣15分钟的频数最多
D.张浩家5月份每次打电话的通话时长在20﹣25分钟的频率为6%
3.将点A(-2,-3)向左平移3个单位,再向上平移2个单位得到点B,则B的坐标是( )
A.(1,-3) B.(-2,1) C.(-5,-1) D.(-5,-5)
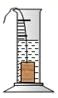
4.如图是小明在物理实验课上用量筒和水测量铁块A的体积实验,小明在匀速向上将铁块提起,直至铁块完全露出水面一定高度的过程中,则下图能反映液面高度h与铁块被提起的时间t之间的函数关系的大致图象是( )
A.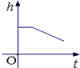 B.
B.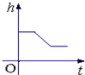 C.
C.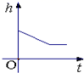 D.
D.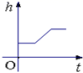
5.某公园草坪的防护栏由100段形状相同的抛物线形构件组成,为了牢固起见,每段护栏需要间距0.4m加设一根不锈钢的支柱,防护栏的最高点距底部0.5m(如图),则这条防护栏需要不锈钢支柱的总长度至少为( )
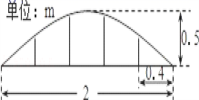
A.50m B.100m C.160m D.200m
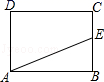
6.如图,矩形ABCD中,AB=4,BC=3,动点E从B点出发,沿B﹣C﹣D﹣A运动至A点停止,设运动的路程为x,△ABE的面积为y,则y与x的函数关系用图象表示正确的是( )
A.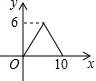 B.
B.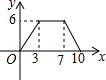 C.
C.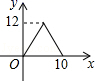 D.
D.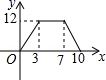
7.反比例函数![]() 经过点(1,
经过点(1,![]() ),则
),则![]() 的值为( )
的值为( )
A.3 B.![]() C.
C.![]() D.
D.![]()
8.下列函数的图象经过![]()
![]() ,且
,且![]() 随
随![]() 的增大而减小的是( )
的增大而减小的是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
9.在菱形![]() 中,
中,![]() ,点
,点![]() 为
为![]() 边的中点,点
边的中点,点![]() 与点
与点![]() 关于
关于![]() 对称,连接
对称,连接![]() 、
、![]() 、
、![]() ,下列结论:①
,下列结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() ,其中正确的是( )
,其中正确的是( )
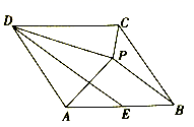
A.①② B.①②③ C.①②④ D.①②③④
10.函数![]() 中,自变量x的取值范围是( )
中,自变量x的取值范围是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
二、填空题(本大题共有6小题,每小题3分,共18分)
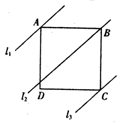
11.如图,四边形![]() 是正方形,直线
是正方形,直线![]() 分别过
分别过![]() 三点,且
三点,且![]() ,若
,若![]() 与
与![]() 的距离为6,正方形
的距离为6,正方形![]() 的边长为10,则
的边长为10,则![]() 与
与![]() 的距离为_________________.
的距离为_________________.
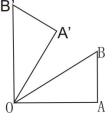
12.如图,∠A=90°,∠AOB=30°,AB=2,△![]() 可以看作由△AOB绕点O逆时针旋转60°得到的,则点
可以看作由△AOB绕点O逆时针旋转60°得到的,则点![]() 与点B的距离为_______.
与点B的距离为_______.
13.今有三部自动换币机,其中甲机总是将一枚硬币换成2枚其他硬币;乙机总是将一枚硬币换成4枚其他硬币;丙机总是将一枚硬币换面10枚其他硬币.某人共进行了12次换币,便将一枚硬币换成了81枚.试问他在丙机上换了_____次?
14.将直线![]() 平移后经过点(5,
平移后经过点(5,![]() ),则平移后的直线解析式为______________.
),则平移后的直线解析式为______________.
15.李老师到超市买了xkg香蕉,花费m元钱;ykg苹果,花费n元钱.若李老师要买3kg香蕉和2kg苹果共需花费_____元.
16.如图,直线l1∥l2∥l3,直线AC分别交l1,l2,l3于点A,B,C;直线DF分别交l1,l2,l3于点D,E,F.AC与DF相交于点H,且AH=2,HB=1,BC=5,则![]() 的值为
的值为

三、解下列各题(本大题共8小题,共72分)
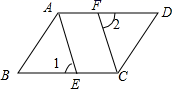
17.(8分)如图,在▱ABCD中,E、F分别是BC、AD边上的点,且∠1=∠1.求证:四边形AECF是平行四边形.
18.(8分)已知函数![]() ,
,
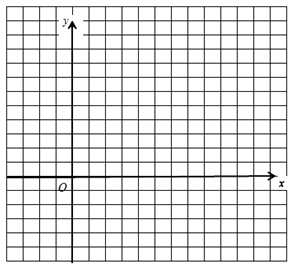
(1)在平面直角坐标系中画出函数图象;
(2)函数图象与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,已知
,已知![]() 是图象上一个动点,若
是图象上一个动点,若![]() 的面积为
的面积为![]() ,求
,求![]() 点坐标;
点坐标;
(3)已知直线![]() 与该函数图象有两个交点,求
与该函数图象有两个交点,求![]() 的取值范围.
的取值范围.
19.(8分)如图,正方形![]() ,点
,点![]() 在边
在边![]() 上,
上,![]() 为等腰直角三角形.
为等腰直角三角形.
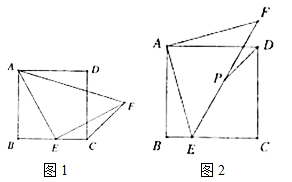
(1)如图1,当![]() ,求证
,求证![]() ;
;
(2)如图2,当![]() ,取
,取![]() 的中点
的中点![]() ,连接
,连接![]() ,求证:
,求证:![]()
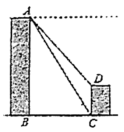
20.(8分)如图,甲、乙两座建筑物的水平距离![]() 为
为![]() ,从甲的顶部
,从甲的顶部![]() 处测得乙的顶部
处测得乙的顶部![]() 处的俯角为48°,测得底部
处的俯角为48°,测得底部![]() 处的俯角为58°,求乙建筑物
处的俯角为58°,求乙建筑物![]() 的高度.(参考数据:
的高度.(参考数据:![]() ,
,![]() ,
,![]() ,
,![]() .结果取整数)
.结果取整数)
21.(8分)先化简,再求值:![]() ,其中x是不等式
,其中x是不等式![]() ≤x﹣3的最小整数解.
≤x﹣3的最小整数解.
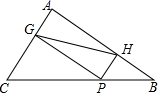
22.(10分)如图,在△ABC中,AC=9,AB=12,BC=15,P为BC边上一动点,PG⊥AC于点G,PH⊥AB于点H.
(1)求证:四边形AGPH是矩形;
(2)在点P的运动过程中,GH的长度是否存在最小值?若存在,请求出最小值,若不存在,请说明理由.
23.(10分)某校![]() 名学生参加植树活动,要求每人植
名学生参加植树活动,要求每人植![]() 棵,活动结束后随机抽查了
棵,活动结束后随机抽查了![]() 名学生每人的植树量,并分为四种类型,
名学生每人的植树量,并分为四种类型,![]() :
:![]() 棵;
棵;![]() ;
;![]() 棵;
棵;![]() :
:![]() 棵,
棵,![]() :
:![]() 棵。将各类的人绘制成扇形图(如图1)和条形图(如图2),经确认扇形图是正确的,而条形图尚有一处错误。
棵。将各类的人绘制成扇形图(如图1)和条形图(如图2),经确认扇形图是正确的,而条形图尚有一处错误。
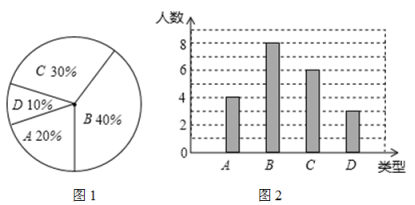
回答下列问题:
(1)写出条形图中存在的错误,并说明理由.
(2)写出这![]() 名学生每人植树量的众数、中位数.
名学生每人植树量的众数、中位数.
(3)在求这![]() 名学生每人植树量的平均数.
名学生每人植树量的平均数.
(4)估计这![]() 名学生共植树多少棵.
名学生共植树多少棵.
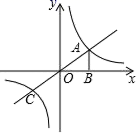
24.(12分)如图,平面直角坐标系中,反比例函数y1=![]() 的图象与函数y2=mx图象交于点A,过点A作AB⊥x轴于点B,已知点A坐标(2,1).
的图象与函数y2=mx图象交于点A,过点A作AB⊥x轴于点B,已知点A坐标(2,1).
(1)求反比例函数解析式;
(2)当y2>y1时,求x的取值范围.
参考答案
一、选择题(每小题3分,共30分)
1、C
2、D
3、C
4、B
5、C
6、B
7、B
8、D
9、C
10、B
二、填空题(本大题共有6小题,每小题3分,共18分)
11、1
12、1
13、8
14、y=2x-1
15、![]()
16、![]()
三、解下列各题(本大题共8小题,共72分)
17、详见解析
18、(1)图略;(2)![]() 或
或![]() ;(3)
;(3)![]() 的取值范围是
的取值范围是![]() 或
或![]() .
.
19、(1)见解析;(2)见解析.
20、38m.
21、![]()
22、 (1)证明见解析;(2)见解析.
23、(1)D;(2)5,5;(3)这![]() 名学生每人植树量的平均数5.3;(4)估计这260名学生共植树1378棵.
名学生每人植树量的平均数5.3;(4)估计这260名学生共植树1378棵.
24、(1)反比例函数的解析式为y=![]() ;(1)﹣1<x<0或x>1.
;(1)﹣1<x<0或x>1.
.
2023-2024学年山西省吕梁柳林县联考数学九年级第一学期期末学业质量监测试题含答案: 这是一份2023-2024学年山西省吕梁柳林县联考数学九年级第一学期期末学业质量监测试题含答案,共7页。试卷主要包含了抛物线的顶点在等内容,欢迎下载使用。
2023-2024学年山西省吕梁柳林县联考数学九上期末教学质量检测模拟试题含答案: 这是一份2023-2024学年山西省吕梁柳林县联考数学九上期末教学质量检测模拟试题含答案,共8页。试卷主要包含了一副三角尺按如图的位置摆放,下列事件中,是必然事件的是等内容,欢迎下载使用。
2023-2024学年山西省吕梁柳林县联考八年级数学第一学期期末学业水平测试试题含答案: 这是一份2023-2024学年山西省吕梁柳林县联考八年级数学第一学期期末学业水平测试试题含答案,共7页。试卷主要包含了答题时请按要求用笔,如图,,,,则的长度为等内容,欢迎下载使用。












