


黄埔区广附2022-2023学年七年级数学第二学期期末考试模拟试题含答案
展开黄埔区广附2022-2023学年七年级数学第二学期期末考试模拟试题
(时间:120分钟 分数:120分)
学校_______ 年级_______ 姓名_______
注意事项
1.考试结束后,请将本试卷和答题卡一并交回.
2.答题前,请务必将自己的姓名、准考证号用0.5毫米黑色墨水的签字笔填写在试卷及答题卡的规定位置.
3.请认真核对监考员在答题卡上所粘贴的条形码上的姓名、准考证号与本人是否相符.
4.作答选择题,必须用2B铅笔将答题卡上对应选项的方框涂满、涂黑;如需改动,请用橡皮擦干净后,再选涂其他答案.作答非选择题,必须用05毫米黑色墨水的签字笔在答题卡上的指定位置作答,在其他位置作答一律无效.
5.如需作图,须用2B铅笔绘、写清楚,线条、符号等须加黑、加粗.
一、选择题(每小题3分,共30分)
1.下面四个二次根式中,最简二次根式是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
2.要使分式![]() 有意义,则 x 的取值范围是( ).
有意义,则 x 的取值范围是( ).
A.x≠±1 B.x≠-1 C.x≠0 D.x≠1
3.下列方程,是一元二次方程的是( )
①![]() , ②
, ②![]() , ③
, ③![]() , ④
, ④ ![]()
A.①② B.①②④ C.①③④ D.②④
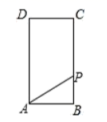
4.如图,矩形![]() 中,
中,![]() ,
,![]() ,点
,点![]() 从点
从点![]() 出发,沿
出发,沿![]() 向终点
向终点![]() 匀速运动.设点
匀速运动.设点![]() 走过的路程为
走过的路程为![]() ,
,![]() 的面积为
的面积为![]() ,能正确反映
,能正确反映![]() 与
与![]() 之间函数关系的图象是( )
之间函数关系的图象是( )
A.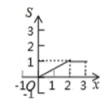 B.
B.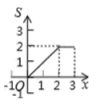
C.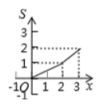 D.
D.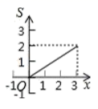
5.如图,在菱形ABCD中,∠A=110°,E,F分别是边AB和BC的中点,EP⊥CD于点P,则∠FPC=( )
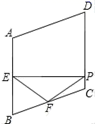
A.35° B.45° C.50° D.55°
6.函数y=![]() 中自变量x的取值范围为( )
中自变量x的取值范围为( )
A.x≥0 B.x≥-1 C.x>-1 D.x≥1
7.等式![]() 成立的x的取值范围在数轴上可表示为( )
成立的x的取值范围在数轴上可表示为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
8.若![]() 是分式方程
是分式方程![]() 的根,则
的根,则![]() 的值为( )
的值为( )
A.9 B.![]() C.13 D.
C.13 D.![]()
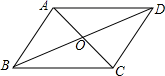
9.如图,在![]() 中,对角线
中,对角线![]() ,
,![]() 交于点
交于点![]() .若
.若![]() ,
,![]() ,
,![]() ,则
,则![]() 的周长为( )
的周长为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
10.笔记本每本a元,买3本笔记本共支出y元,在这个问题中:
①a是常量时,y是变量;
②a是变量时,y是常量;
③a是变量时,y也是变量;
④a,y可以都是常量或都是变量.
上述判断正确的有( )
A.1个 B.2个 C.3个 D.4个
二、填空题(本大题共有6小题,每小题3分,共18分)
11.李明同学进行射击练习,两发子弹各打中5环,四发子弹各打中8环,三发子弹各打中9环.一发子弹打中10环,则他射击的平均成绩是________环.
12.已知关于 ![]() 的方程
的方程![]() ,如果设
,如果设![]() ,那么原方程化为关于
,那么原方程化为关于![]() 的方程是____.
的方程是____.
13.已知一个样本中共5个数据,其中前四个数据的权数分别为0.2,0.3,0.2,0.1,则余下的一个数据对应的权数为________.
14.如果等腰梯形两底差的一半等于它的高,那么此梯形较小的一个底角等于_________度.
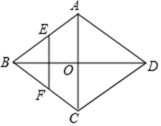
15.如图,菱形ABCD中,对角线AC,BD相交于点O,点E,F分别是的边AB,BC边的中点![]() 若
若![]() ,
,
![]() ,则线段EF的长为______.
,则线段EF的长为______.
16.直线![]() 与两坐标轴围成的三角形的面积为4,则
与两坐标轴围成的三角形的面积为4,则![]() 的值为______.
的值为______.
三、解下列各题(本大题共8小题,共72分)
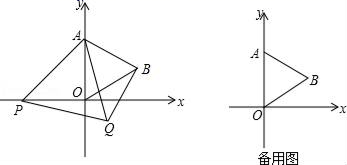
17.(8分)如图在平面直角坐标系中,已知点A(0,2![]() ),△AOB为等边三角形,P是x轴负半轴上一个动点(不与原点O重合),以线段AP为一边在其右侧作等边三角形△APQ.
),△AOB为等边三角形,P是x轴负半轴上一个动点(不与原点O重合),以线段AP为一边在其右侧作等边三角形△APQ.
(1)求点B的坐标;
(2)在点P的运动过程中,∠ABQ的大小是否发生改变?如不改变,求出其大小:如改变,请说明理由;
(3)连接OQ,当OQ∥AB时,求P点的坐标.
18.(8分)解方程:(1)x(2x+3)=4x+6
计算:(2)![]()
(3)![]()
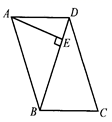
19.(8分)如图,在平行四边形![]() 中,
中,![]() ,
,![]() 于点
于点![]() ,试求
,试求![]() 的度数.
的度数.
20.(8分)学校需要添置教师办公桌椅A、B两型共200套,已知2套A型桌椅和1套B型桌椅共需2000元,1套A型桌椅和3套B型桌椅共需3000元.
(1)求A,B两型桌椅的单价;
(2)若需要A型桌椅不少于120套,B型桌椅不少于70套,平均每套桌椅需要运费10元.设购买A型桌椅x套时,总费用为y元,求y与x的函数关系式,并直接写出x的取值范围;
(3)求出总费用最少的购置方案.
21.(8分)计算:
(1)![]()
(2)(![]() )﹣(
)﹣(![]() )
)
22.(10分)(1)分解因式:①![]() ②
②![]()
(2)解不等式组,并把解集在数轴上表示出来. 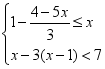
23.(10分)小明到服装店参加社会实践活动,服装店经理让小明帮助解决以下问题:
服装店准备购进甲乙两种服装,甲种每件进价80元,售价120元;乙种每件进价60元,售价90元.计划购进两种服装共100件,其中甲种服装不少于65件.
(1)若购进这100件服装的费用不得超过7500,则甲种服装最多购进多少件?
(2)在(1)的条件下,该服装店对甲种服装以每件优惠a(0<a<20)元的价格进行优惠促销活动,乙种服装价格不变,那么该服装店应如何调整进货方案才能获得最大利润?
24.(12分)某工厂计划生产甲、乙两种产品共2500吨,每生产1吨甲产品可获得利润0.3万元,每生产1吨乙产品可获得利润0.4万元.设该工厂生产了甲产品x(吨),生产甲、乙两种产品获得的总利润为y(万元).
(1)求y与x之间的函数表达式;
(2)若每生产1吨甲产品需要A原料0.25吨,每生产1吨乙产品需要A原料0.5吨.受市场影响,该厂能获得的A原料至多为1000吨,其它原料充足.求出该工厂生产甲、乙两种产品各为多少吨时,能获得最大利润.
参考答案
一、选择题(每小题3分,共30分)
1、A
2、D
3、D
4、A
5、D
6、B
7、B
8、B
9、B
10、B
二、填空题(本大题共有6小题,每小题3分,共18分)
11、7.9
12、![]() .
.
13、0.1
14、1
15、3
16、![]()
三、解下列各题(本大题共8小题,共72分)
17、 (1)点B的坐标为B(3,![]() );(2)∠ABQ=90°,始终不变,理由见解析;(3)P的坐标为(﹣3,0).
);(2)∠ABQ=90°,始终不变,理由见解析;(3)P的坐标为(﹣3,0).
18、(1)![]() (2)
(2)![]() ;(3)
;(3)![]()
19、![]() .
.
20、(1)A,B两型桌椅的单价分别为600元,800元;(2)y=﹣200x+162000(120≤x≤130);(3)购买A型桌椅130套,购买B型桌椅70套,总费用最少,最少费用为136000元.
21、(1)-1;(2)2![]() +3
+3![]() .
.
22、 (1)① ![]() ;②
;②![]() ;(2)
;(2)![]()
23、(1)75件(2)当x=65时,w有最大值,则购进甲种服装65件,乙种服装35件
24、(1)![]() ;(2)工厂生产甲产品1000吨,乙产品1500吨时,能获得最大利润.
;(2)工厂生产甲产品1000吨,乙产品1500吨时,能获得最大利润.
黄埔区广附2023-2024学年数学九上期末预测试题含答案: 这是一份黄埔区广附2023-2024学年数学九上期末预测试题含答案,共6页。试卷主要包含了考生必须保证答题卡的整洁,平面直角坐标系内与点P,一元二次方程的解是等内容,欢迎下载使用。
广东省黄埔区广附2023-2024学年数学九上期末综合测试模拟试题含答案: 这是一份广东省黄埔区广附2023-2024学年数学九上期末综合测试模拟试题含答案,共8页。
广东省黄埔区广附2023-2024学年八上数学期末质量检测模拟试题含答案: 这是一份广东省黄埔区广附2023-2024学年八上数学期末质量检测模拟试题含答案,共7页。试卷主要包含了如图,中的周长为,下列各式中,分式的个数为等内容,欢迎下载使用。












