


贵州省兴仁县黔龙学校2022-2023学年数学七下期末监测试题含答案
展开贵州省兴仁县黔龙学校2022-2023学年数学七下期末监测试题
(时间:120分钟 分数:120分)
学校_______ 年级_______ 姓名_______
请考生注意:
1.请用2B铅笔将选择题答案涂填在答题纸相应位置上,请用0.5毫米及以上黑色字迹的钢笔或签字笔将主观题的答案写在答题纸相应的答题区内。写在试题卷、草稿纸上均无效。
2.答题前,认真阅读答题纸上的《注意事项》,按规定答题。
一、选择题(每小题3分,共30分)
1.已知![]() ,
,![]() ,且
,且![]() ,若
,若![]() ,
,![]() ,则
,则![]() 的长为( )
的长为( )
A.4 B.9 C.![]() D.
D.![]()
2.点(1,m),(2,n)都在函数y=﹣2x+1的图象上,则m、n的大小关系是( )
A.m=n B.m<n C.m>n D.不确定
3.方程![]() 有( )
有( )
A.两个不相等的实数根 B.两个相等的实数根 C.无实数根 D.无法确定
4.在平面直角坐标系中,反比例函数![]() 的图象上有三点
的图象上有三点![]() ,若
,若![]() 且
且![]() ,则
,则![]() 的取值范围为( )
的取值范围为( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
5.下表记录了甲、乙、丙、丁四名同学最近几次数学考试成绩的平均数与方差:
| 甲 | 乙 | 丙 | 丁 |
平均数(分) | 92 | 95 | 95 | 92 |
方差 | 3.6 | 3.6 | 7.4 | 8.1 |
要选择一名成绩好且发挥稳定的同学参加数学比赛,应该选择( )
A.甲 B.乙 C.丙 D.丁
6.如图,小靓用七巧板拼成一幅装饰图,放入长方形ABCD内,装饰图中的三角形顶点E,F分别在边AB,BC上,△GHD的边GD在边AD上,则![]() 的值为( )
的值为( )
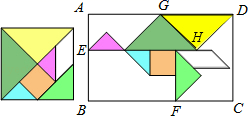
A.![]() B.4
B.4![]() ﹣4 C.
﹣4 C.![]() D.
D.![]()
7.下列式子中一定是二次根式的是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
8.如图,平行四边形ABCD中,![]() ,点E为BC边中点,
,点E为BC边中点,![]() ,则AE的长为 ( )
,则AE的长为 ( )
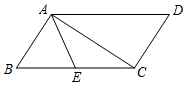
A.2cm B.3cm C.4cm D.6cm
9.如图,在平面直角坐标系中,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() ,以点
,以点![]() 为圆心,
为圆心,![]() 长为半径画弧,交
长为半径画弧,交![]() 轴的负半轴于点
轴的负半轴于点![]() ,则点
,则点![]() 的坐标为( )
的坐标为( )
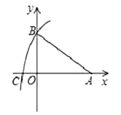
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
10.下列式子中,属于最简二次根式的是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
二、填空题(本大题共有6小题,每小题3分,共18分)
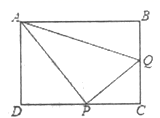
11.如图,已知矩形![]() ,
,![]() ,
,![]() ,点
,点![]() 为
为![]() 中点,在
中点,在![]() 上取一点
上取一点![]() ,使
,使![]() 的面积等于
的面积等于![]() ,则
,则![]() 的长度为_______.
的长度为_______.
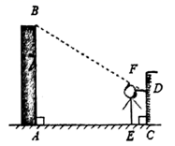
12.如图,小明想利用太阳光测量楼高,发现对面墙上有这栋楼的影子,小明边移动边观察,发现站到点E处时,可以使自己落在墙上的影子与这栋楼落在墙上的影子重叠且高度恰好相同.此时测得墙上影子高![]() ,
,![]() ,
,![]() (点A、E、C在同一直线上).已知小明身高EF是1.6m,则楼高AB为______m.
(点A、E、C在同一直线上).已知小明身高EF是1.6m,则楼高AB为______m.
13.点A(-2,3)关于x轴对称的点B的坐标是_____
14.已知平行四边形ABCD中,∠B+∠D=270°,则∠C=________.
15.比较大小:![]() __________
__________![]() .(用不等号连接)
.(用不等号连接)
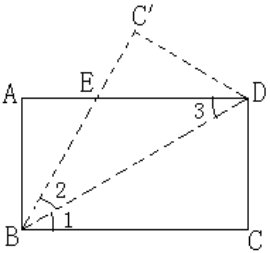
16.如图,已知矩形ABCD沿着直线BD折叠,使点C落在C/处,BC/交AD于E,AD=8,AB=4,DE的长=________________.
三、解下列各题(本大题共8小题,共72分)
17.(8分)如图,直线y=2x+3与x轴相交于点A,与y轴相交于点B.
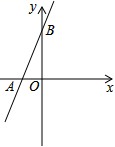
(1)求A,B两点的坐标;
(2)过B点作直线BP与x轴相交于P,且使OP=2OA, 求直线BP的解析式.
18.(8分)如图,![]() 中任意一点
中任意一点![]() 经平移后对应点为
经平移后对应点为![]() ,将
,将![]() 作同样的平移得到
作同样的平移得到![]() ,其中点A与点D,点B与点E,点C与点F分别对应,请解答下列问题:
,其中点A与点D,点B与点E,点C与点F分别对应,请解答下列问题:
(1)画出![]() ,并写出点D、E、F的坐标..
,并写出点D、E、F的坐标..
(2)若![]() 与
与![]() 关于原点O成中心对称,直接写出点D的对应点
关于原点O成中心对称,直接写出点D的对应点![]() 的坐标.
的坐标.
19.(8分)如图,已知一次函数y1=ax+b的图象与x轴、y轴分别交于点D、C,与反比例函数y2=![]() 的图象交于A、B两点,且点A的坐标是(1,3)、点B的坐标是(3,m).
的图象交于A、B两点,且点A的坐标是(1,3)、点B的坐标是(3,m).
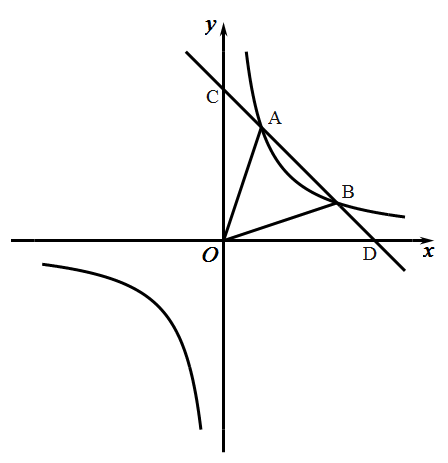
(1)求一次函数与反比例函数的解析式;
(2)求C、D两点的坐标,并求△AOB的面积;
(3)根据图象直接写出:当x在什么取值范围时,y1>y2?
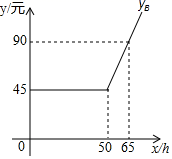
20.(8分)某通信公司策划了![]() 两种上网的月收费方式:
两种上网的月收费方式:
收费方式 | 月使用费/元 | 包时上网时间/ | 超时费/(元/ |
| 30 | 25 | 0.05 |
|
|
|
|
设每月上网时间为![]() ,方式
,方式![]() 的收费金额分别为
的收费金额分别为![]() (元),
(元),![]() (元),如图是
(元),如图是![]() 与
与![]() 之间函数关系的图象.(友情提示:若累计上网时间不超出包时上网时间,则只收月使用费;若累计上网时间超出包时上网时间,则对超出部分再加收超时费)
之间函数关系的图象.(友情提示:若累计上网时间不超出包时上网时间,则只收月使用费;若累计上网时间超出包时上网时间,则对超出部分再加收超时费)
(1)![]() ,
,![]() ,
,![]() ;
;
(2)求![]() 与
与![]() 之间的函数解析式;
之间的函数解析式;
(3)若每月上网时间为31小时,请直接写出选择哪种方式能节省上网费.
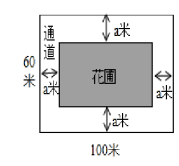
21.(8分)如图,为美化校园环境,某校计划在一块长为100米,宽为60米的长方形空地上修建一个长方形花圃,并将花圃四周余下的空地修建成同样宽的通道,设通道宽为![]() 米.
米.
(1)如果通道所占面积是整个长方形空地面积的![]() ,求出此时通道的宽;
,求出此时通道的宽;
(2)如果通道宽![]() (米)的值能使关于
(米)的值能使关于![]() 的方程
的方程![]() 有两个相等的实数根,并要求修建的通道的宽度不少于5米且不超过12米,求出此时通道的宽.
有两个相等的实数根,并要求修建的通道的宽度不少于5米且不超过12米,求出此时通道的宽.
22.(10分)数形结合是一种重要的数学思想,我们不但可以用数来解决图形问题,同样也可以用借助图形来解决数量问题,往往能出奇制胜,数轴和勾股定理是数形结合的典范.数轴上的两点A和B所表示的数分别是![]() 和
和![]() ,则A,B两点之间的距离
,则A,B两点之间的距离![]() ;坐标平面内两点
;坐标平面内两点![]() ,
,![]() ,它们之间的距离
,它们之间的距离![]() .如点
.如点![]() ,
,![]() ,则
,则![]()
![]() .
.![]() 表示点
表示点![]() 与点
与点![]() 之间的距离,
之间的距离,![]()
![]() 表示点
表示点![]() 与点
与点![]() 和
和![]() 的距离之和.
的距离之和.
(1)已知点![]() ,
,![]() ,
,![]() ________;
________;
(2)![]() 表示点
表示点![]() 和点
和点![]() 之间的距离;
之间的距离;
(3)请借助图形,求![]() 的最小值.
的最小值.
23.(10分)如图,已知函数![]() 和
和![]() 的图象交于点
的图象交于点![]() ,这两个函数的图象与
,这两个函数的图象与![]() 轴分别交于点
轴分别交于点![]() 、
、![]() .
.
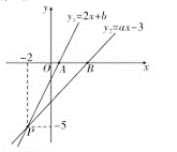
(1)分别求出这两个函数的解析式;
(2)求![]() 的面积;
的面积;
(3)根据图象直接写出![]() 时,
时,![]() 的取值范围.
的取值范围.
24.(12分)下图是某汽车行驶的路程![]()
![]() 与时间
与时间![]() (分钟)的函数关系图.
(分钟)的函数关系图.
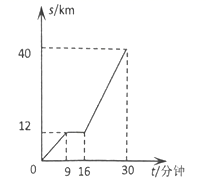
观察图中所提供的信息,解答下列问题:
(1)汽车在前![]() 分钟内的平均速度是 .
分钟内的平均速度是 .
(2)汽车在中途停了多长时间?
(3)当![]() 时,求
时,求![]() 与
与![]() 的函数关系式
的函数关系式
参考答案
一、选择题(每小题3分,共30分)
1、B
2、C
3、A
4、D
5、B
6、A
7、A
8、B
9、B
10、D
二、填空题(本大题共有6小题,每小题3分,共18分)
11、![]()
12、21.2
13、(-2,-3).
14、45°
15、<
16、5
三、解下列各题(本大题共8小题,共72分)
17、(1)(-![]() ,0);(0,1);(2)y=x+1或y=-x+1.
,0);(0,1);(2)y=x+1或y=-x+1.
18、(1)D(0,4),E(2,2),F(3,5),画图见解析;(2)(0,-4)
19、(1)y1=![]() ,y1=﹣x+4;(1)4;(3)当 x 满足 1<x<3 、x<2时,则 y1>y1.
,y1=﹣x+4;(1)4;(3)当 x 满足 1<x<3 、x<2时,则 y1>y1.
20、(1)45,50,0.05;(2)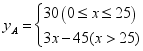 ;(3)若每月上网的时间为31小时,选择方式B能节省上网费.
;(3)若每月上网的时间为31小时,选择方式B能节省上网费.
21、(1)5米;(2)1米;
22、(1)![]() ;(2)
;(2)![]() ,
,![]() ,
,![]() ;(3)最小值是
;(3)最小值是![]() .
.
23、 (1)![]() ,
,![]() ;(2)S△ABC=
;(2)S△ABC=![]() ;(3)
;(3)![]() 时,
时,![]() .
.
24、(1) ![]() ;(2)7分钟;(3)
;(2)7分钟;(3)![]() .
.
贵州省兴仁县黔龙学校2023-2024学年九上数学期末达标测试试题含答案: 这是一份贵州省兴仁县黔龙学校2023-2024学年九上数学期末达标测试试题含答案,共9页。
贵州省兴仁县黔龙学校2023-2024学年八年级数学第一学期期末教学质量检测模拟试题含答案: 这是一份贵州省兴仁县黔龙学校2023-2024学年八年级数学第一学期期末教学质量检测模拟试题含答案,共7页。试卷主要包含了点在,下列计算不正确的是,下列计算中正确的是等内容,欢迎下载使用。
贵州省兴仁市黔龙、黔峰、金成学校2022-2023学年七年级上学期期中质量检测数学试题(含答案): 这是一份贵州省兴仁市黔龙、黔峰、金成学校2022-2023学年七年级上学期期中质量检测数学试题(含答案),共5页。试卷主要包含了下列互为倒数的是,将多项式按x的降幂排列的结果为,下列解方程的变形过程正确的是等内容,欢迎下载使用。












