


湖南长沙市青竹湖湘一外国语学校2022-2023学年数学七年级第二学期期末学业质量监测模拟试题含答案
展开湖南长沙市青竹湖湘一外国语学校2022-2023学年数学七年级第二学期期末学业质量监测模拟试题
(时间:120分钟 分数:120分)
学校_______ 年级_______ 姓名_______
考生须知:
1.全卷分选择题和非选择题两部分,全部在答题纸上作答。选择题必须用2B铅笔填涂;非选择题的答案必须用黑色字迹的钢笔或答字笔写在“答题纸”相应位置上。
2.请用黑色字迹的钢笔或答字笔在“答题纸”上先填写姓名和准考证号。
3.保持卡面清洁,不要折叠,不要弄破、弄皱,在草稿纸、试题卷上答题无效。
一、选择题:本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.某课外兴趣小组为了解所在地区老年人的健康情况,分别作了四种不同的抽样调查,你认为抽样比较合理的是( )
A.调查了10名老年邻居的健康状况
B.在医院调查了1000名老年人的健康状况
C.在公园调查了1000名老年人的健康状况
D.利用派出所的户籍网随机调查了该地区10%的老年人的健康状况
2.某机械厂七月份生产零件50万个,第三季度生产零件196万个.设该厂八、九月份平均每月的增长率为x,那么x满足的方程是
A.50(1+x2)=196 B.50+50(1+x2)=196
C.50+50(1+x)+50(1+x)2=196 D.50+50(1+x)+50(1+2x)=196
3.在下列性质中,平行四边形不一定具有的是( )
A.对边相等 B.对边平行 C.对角互补 D.内角和为360°
4.下列方程有两个相等的实数根的是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
5.下面几组条件中,能判断一个四边形是平行四边形的是( )
A.一组对边相等 B.两条对角线互相平分
C.一组对边平行 D.两条对角线互相垂直
6.若直线y=kx+b经过一、二、四象限,则直线y=bx﹣k的图象只能是图中的( )
A.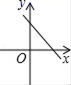 B.
B.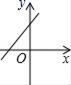 C.
C.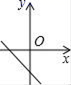 D.
D.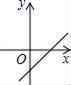
7.设![]() ,
,![]() ,则
,则![]() 与
与![]() 的大小关系是( )
的大小关系是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
8.如图直线l1:y=ax+b,与直线l2:y=mx+n交于点A(1,3),那么不等式ax+b<mx+n的解集是( )
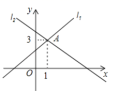
A.x>3 ![]() B.x<3
B.x<3 ![]() C.x>1
C.x>1 ![]() D.x<1
D.x<1
9.如图,BP平分∠ABC,D为BP上一点,E,F分别在BA,BC上,且满足DE=DF,若∠BED=140°,则∠BFD的度数是( )
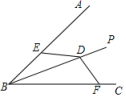
A.40° B.50° C.60° D.70°
10.民族图案是数学文化中的一块瑰宝.下列图案中,既不是中心对称图形也不是轴对称图形的是( )
A. B.
B.
C. D.
D.
11.一次函数![]() 的图象经过原点,则k的值为
的图象经过原点,则k的值为![]()
![]()
A.2 B.![]() C.2或
C.2或![]() D.3
D.3
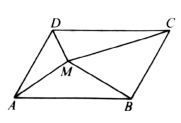
12.已知点![]() 是平行四边形
是平行四边形![]() 内一点(不含边界),设
内一点(不含边界),设![]()
![]()
![]() .若
.若![]()
![]()
![]() ,则( )
,则( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
二、填空题(每题4分,满分20分,将答案填在答题纸上)
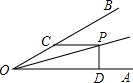
13.如图,∠AOP=∠BOP=15°,PC∥OA,PD⊥OA,若PD=3cm,则PC的长为_____cm.
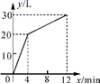
14.一个有进水管和出水管的容器,从某时刻开始4 min内只进水不出水,在随后的8 min内既进水又出水,每分钟的进水量和出水量是两个常数,容器内的水量y(L)与时间x(min)之间的关系如图所示,则每分钟的出水量为________________
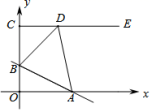
15.如图,在平面直角坐标系![]() 中,点
中,点![]() ,射线
,射线![]() 轴,直线
轴,直线![]() 交线段
交线段![]() 于点
于点![]() ,交
,交![]() 轴于点
轴于点![]() ,
,![]() 是射线
是射线![]() 上一点.若存在点
上一点.若存在点![]() ,使得
,使得![]() 恰为等腰直角三角形,则
恰为等腰直角三角形,则![]() 的值为_______.
的值为_______.
16.关于![]() 的函数
的函数![]() (其中
(其中![]() )是一次函数,那么
)是一次函数,那么![]() =_______。
=_______。
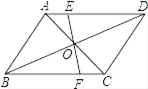
17.如图,平行四边形ABCD的对角线AC,BD交于O,EF过点O与AD,BC分别交于E,F,若AB=4,BC=5,OE=1.5,则四边形EFCD的周长_____.
三、解答题 (本大题共7小题,共64分.解答应写出文字说明、证明过程或演算步骤.)
18.(5分)旅客乘乘车按规定可以随身携带一定质量的行李,如果超过规定,则需购买行李票,设行李票y(元)是行李质量x(千克)的一次函数.其图象如图所示.
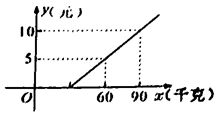
(1)当旅客需要购买行李票时,求出y与x之间的函数关系式;
(2)当旅客不愿意购买行李票时,最多可以携带多少行李?
19.(5分)如图1,在△ABC中,AB=BC=5,AC=6,△ABC沿BC方向向右平移得△DCE,A、C对应点分别是D、E.AC与BD相交于点O.
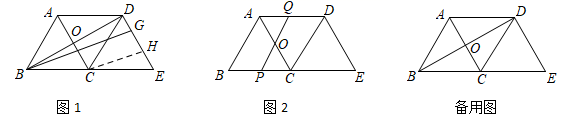
(1)将射线BD绕B点顺时针旋转,且与DC,DE分别相交于F,G,CH∥BG交DE于H,当DF=CF时,求DG的长;
(2)如图2,将直线BD绕点O逆时针旋转,与线段AD,BC分别相交于点Q,P.设OQ=x,四边形ABPQ的周长为y,求y与x之间的函数关系式,并求y的最小值.
(3)在(2)中PQ的旋转过程中,△AOQ是否构成等腰三角形?若能构成等腰三角形,求出此时PQ的长?若不能,请说明理由.
20.(8分)阅读下列材料:
在因式分解中,把多项式中某些部分看作一个整体,用一个新的字母代替(即换元),不仅可以简化要分解的多项式的结构,而且能使式子的特点更加明显,便于观察如何进行因式分解,我们把这种因式分解的方法称为“换元法”.
下面是小涵同学用换元法对多项式(x2﹣4x+1)(x2﹣4x+7)+9进行因式分解的过程.
解:设x2﹣4x=y
原式=(y+1)(y+7)+9(第一步)
=y2+8y+16(第二步)
=(y+4)2(第三步)
=(x2﹣4x+4)2(第四步)
请根据上述材料回答下列问题:
(1)小涵同学的解法中,第二步到第三步运用了因式分解的 ;
A.提取公因式法 B.平方差公式法 C.完全平方公式法
(2)老师说,小涵同学因式分解的结果不彻底,请你写出该因式分解的最后结果: ;
(3)请你用换元法对多项式(x2+2x)(x2+2x+2)+1进行因式分解.
21.(10分)某地区2014年投入教育经费2500万元,2016年投入教育经费3025万元,求2014年至2016年该地区投入教育经费的年平均增长率.
22.(10分)一家公司准备招聘一名英文翻译,对甲、乙和丙三名应试者进行了听、说、读、写 的英语水平测试,他们各项的成绩(百分制)如下:
应试者 | 听 | 说 | 读 | 写 |
甲 | 82 | 86 | 78 | 75 |
乙 | 73 | 80 | 85 | 82 |
丙 | 81 | 82 | 80 | 79 |
(1)如果这家公司按照这三名应试者的平均成绩(百分制)计算,从他们的成绩看,应该录取谁?
(2)如果这家公司想招一名口语能力较强的翻译,听、说、读、写成绩按照 3∶4∶2∶1 的权重确定,计算三名应试者的平均成绩(百分制),从他们的成绩看, 应该录取谁?
(3)如果这家公司想招一名笔译能力较强的翻译,听、说、读、写成绩按照 1∶2∶3∶4 的权重确定,计算三名应试者的平均成绩(百分制).从他们的成绩看, 应该录取谁?
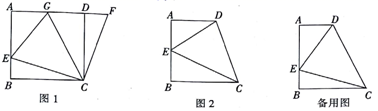
23.(12分)如图1,在正方形ABCD中,点E是AB上一点,点F是AD延长线上一点,且DF=BE,连接CE、CF.
(1)求证:CE=CF.
(2)在图1中,若点G在AD上,且∠GCE=45°,则GE=BE+GD成立吗;为什么;
(3)根据你所学的知识,运用(1)、(2)解答中积累的经验,完成下列各题,如图2,在四边形ABCD中,AD∥BC(BC>AD),∠B=90°,AB=BC,且∠DCE=45°.
①若AE=6,DE=10,求AB的长;
②若AB=BC=9,BE=3,求DE的长.
参考答案
一、选择题:本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1、D
2、C
3、C
4、B
5、B
6、B
7、B
8、D
9、A
10、B
11、A
12、D
二、填空题(每题4分,满分20分,将答案填在答题纸上)
13、1
14、![]() L
L
15、3或6
16、![]() 、
、![]() 、
、![]()
17、1
三、解答题 (本大题共7小题,共64分.解答应写出文字说明、证明过程或演算步骤.)
18、(1)![]() ;(2)当旅客不愿意购买行李票时,最多可以携带30千克行李.
;(2)当旅客不愿意购买行李票时,最多可以携带30千克行李.
19、(1)1;(1)y=1x+10(![]() ≤x≤4),当x=
≤x≤4),当x=![]() 时,y有最小值,最小值为
时,y有最小值,最小值为![]() ;(3)能,满足条件的PQ的值为:
;(3)能,满足条件的PQ的值为:![]() 或2或3.
或2或3.
20、(1)C;(2)(x﹣2)1;(3)(x+1)1.
21、10%.
22、(1) 应该录取丙;(2) 应该录取甲;(3)应该录取乙
23、(1)证明见解析;(2)成立;(3)①12;②7.1
2023-2024学年湖南长沙市青竹湖湘一外国语学校数学九上期末质量检测模拟试题含答案: 这是一份2023-2024学年湖南长沙市青竹湖湘一外国语学校数学九上期末质量检测模拟试题含答案,共8页。试卷主要包含了下列各数中是无理数的是等内容,欢迎下载使用。
2023-2024学年湖南省长沙市青竹湖湘一外国语学校数学九上期末经典模拟试题含答案: 这是一份2023-2024学年湖南省长沙市青竹湖湘一外国语学校数学九上期末经典模拟试题含答案,共7页。试卷主要包含了三角形的内心是,已知二次函数y=mx2+x+m等内容,欢迎下载使用。
湖南省长沙市开福区青竹湖湘一外国语学校2023-2024学年数学八上期末监测试题含答案: 这是一份湖南省长沙市开福区青竹湖湘一外国语学校2023-2024学年数学八上期末监测试题含答案,共7页。试卷主要包含了下列命题是假命题的是,下列式子正确的是等内容,欢迎下载使用。












