攀枝花市重点中学2022-2023学年七下数学期末达标测试试题含答案

攀枝花市重点中学2022-2023学年七下数学期末达标测试试题

（时间：120分钟             分数：120分）

学校_______            年级_______        姓名_______

注意事项

1．考生要认真填写考场号和座位序号。

2．试题所有答案必须填涂或书写在答题卡上，在试卷上作答无效。第一部分必须用2B 铅笔作答；第二部分必须用黑色字迹的签字笔作答。

3．考试结束后，考生须将试卷和答题卡放在桌面上，待监考员收回。

一、选择题(每小题3分,共30分)

1．下列选择中，是直角三角形的三边长的是(　　)

A．1，2，3 B．2，5，3 C．3，4，5 D．4，5，6

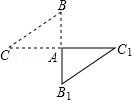
2．如图，在中，，点是的中点，则下列结论不正确的是（    ）

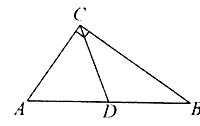
A． B． C． D．

3．△ABC的三边为a、b、c，由下列条件不能判断它是直角三角形的是（　　）

A．∠A: ∠B: ∠C =3∶4∶5 B．∠A=∠B+∠C

C．a2=(b+c)(b-c) D．a:b:c =1∶2∶

4．不能使四边形ABCD是平行四边形是条件是（     ）

A．AB =CD，BC=AD B．AB =CD，

C． D．AB=CD，

5．下列多项式中能用完全平方公式分解的是（    ）

A． B． C． D．

6．甲、乙两人在直线跑道上同起点、同终点、同方向匀速跑步500米，先到终点的人原地休息．已知甲先出发2秒．在跑步过程中，甲、乙两人的距离y（米）与乙出发的时间t（秒）之间的关系如图所示，给出以下结论：①a=8；②b=92；③c=123；④乙的速度比甲的速度快1米/秒，其中正确的编号是(   )

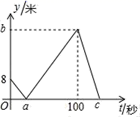
A．①② B．②③ C．①②③ D．①②③④

7．如图，在菱形ABCD中，E，F分别是AB，AC的中点，若EF=2，则菱形ABCD的周长为（   ）

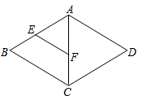
A．16 B．8 C． D．4

8．若二次根式有意义，则x的取值范围是（    ）

A．x≥-5 B．x>-5 C．x≥5 D．x>5

9．某课外兴趣小组为了了解所在学校的学生对体育运动的爱好情况，设计了四种不同的抽样调查方案,你认为比较合理的是(     )

A．在校园内随机选择50名学生

B．从运动场随机选择50名男生

C．从图书馆随机选择50名女生

D．从七年级学生中随机选择50名学生

10．在平面内由极点、极轴和极径组成的坐标系叫做极坐标系．如图，在平面上取定一点O称为极点；从点O出发引一条射线Ox称为极轴；线段OP的长度称为极径．点P的极坐标就可以用线段OP的长度以及从Ox转动到OP的角度（规定逆时针方向转动角度为正）来确定，即P（3，60°）或P（3，﹣300°）或P（3，420°）等，则点P关于点O成中心对称的点Q的极坐标表示不正确的是（　　）

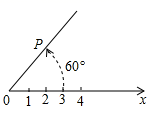
A．Q（3，－120°） B．Q（3，240°） C．Q（3，－500°） D．Q（3，600°）

二、填空题(本大题共有6小题，每小题3分，共18分)

11．如图，将 Rt△ABC 绕直角顶点 A 按顺时针方向旋转 180° 得△AB1C1，写出旋转后 BC 的对应线段_____．

12．已知直线y＝kx＋b和直线y＝－3x平行，且过点（0，－3），则此直线与x轴的交点坐标为________.

13．分解因式______．

14．如图，已知中，，，，是的垂直平分线，交于点，连接，则___

15．方程的根是__________．

16．如图为某楼梯，测得楼梯的长为5米，高3米，计划在楼梯表面铺地毯，地毯的长度至少需要____________米.

三、解下列各题(本大题共8小题，共72分)

17．（8分）用公式法解下列方程：
(1)2x2−4x−1=0；                     
(2)5x+2=3x2.

18．（8分）已知在▱ABCD中，点E、F在对角线BD上，BE＝DF，点M、N在BA、DC延长线上，AM＝CN，连接ME、NF．试判断线段ME与NF的关系，并说明理由．

19．（8分）某商场统计了每个营业员在某月的销售额，绘制了如下的条形统计图以及不完整的扇形统计图：

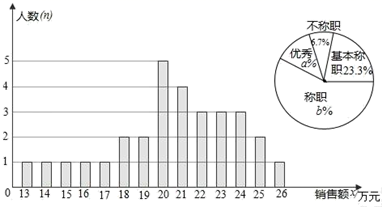
解答下列问题：(1)设营业员的月销售额为x(单位：万元)，商场规定：当x＜15时为不称职，当15≤x＜20时，为基本称职，当20≤x＜25为称职，当x≥25时为优秀．则扇形统计图中的a＝_____，b＝_____．

(2)所有营业员月销售额的中位数和众数分别是多少？

(3)为了调动营业员的积极性，决定制定一个月销售额奖励标准，凡到达或超过这个标准的营业员将受到奖励．如果要使得营业员的半数左右能获奖，奖励标准应定为多少万元？并简述其理由．

20．（8分）如图，直线MN与x轴，y轴分别相交于A，C两点，分别过A，C两点作x轴，y轴的垂线相交于B点，且OA，OC（OA＞OC）的长分别是一元二次方程x2﹣14x+48=0的两个实数根．

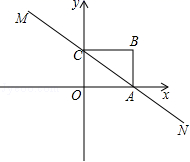
（1）求C点坐标；

（2）求直线MN的解析式；

（3）在直线MN上存在点P，使以点P，B，C三点为顶点的三角形是等腰三角形，请直接写出P点的坐标．

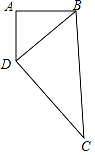
21．（8分）如图，一块四边形的土地，其中∠BAD=90°，AB=4m，BC=12m，CD=13m，AD=3m．

（1）试说明BD⊥BC；

（2）求这块土地的面积．

22．（10分）某班级准备购买一些奖品奖励春季运动会表现突出的同学，奖品分为甲、乙两种，已知，购买一个甲奖品比一个乙奖品多用20元，若用400元购买甲奖品的个数是用160元购买乙奖品个数的一半.

（1）求购买一个甲奖品和一个乙奖品各需多少元？

（2）经商谈，商店决定给予该班级每购买甲奖品3个就赠送一个乙奖品的优惠，如果该班级需要乙奖品的个数是甲奖品的2倍还多8个，且该班级购买两种奖项的总费用不超过640元，那么该班级最多可购买多少个甲奖品？

23．（10分）如图，四边形ABCD中，点E、F、G、H分别是边AB、BC、CD、DA的中点，顺次连接E、F、G、H，得到的四边形EFGH叫中点四边形．

（1）求证：四边形EFGH是平行四边形；

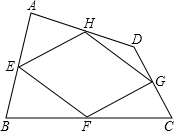
（2）如图，当四边形ABCD变成等腰梯形时，它的中点四边形是菱形，请你探究并填空：

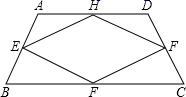
当四边形ABCD变成平行四边形时，它的中点四边形是                ；

当四边形ABCD变成矩形时，它的中点四边形是                  ；

当四边形ABCD变成菱形时，它的中点四边形是                 ；

当四边形ABCD变成正方形时，它的中点四边形是                  ；

（3）根据以上观察探究，请你总结中点四边形的形状由原四边形的什么决定的？

24．（12分）已知，直线与反比例函数交于点，且点的横坐标为4，过轴上一点作垂直于交于点，如图.

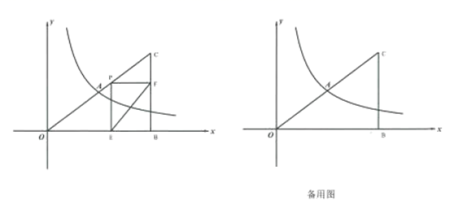
（1）若点是线段上一动点，过点作，，垂足分别于、，求线段长度的最小值.

（2）在（1）的取得最小值的前提下，将沿射线平移，记平移后的三角形为，当时，在平面内存在点，使得、、、四点构成平行四边形，这样的点有几个？直接写出点的坐标.

参考答案

一、选择题(每小题3分,共30分)

1、C

2、D

3、A

4、D

5、B

6、D

7、A

8、C

9、A

10、C

二、填空题(本大题共有6小题，每小题3分，共18分)

11、B1C1．

12、 (−1,0).

13、 (2b+a)(2b-a)

14、5

15、

16、1．

三、解下列各题(本大题共8小题，共72分)

17、 (1) x1=,x2=；(2) x1=2,x2=−.

18、ME＝NF且ME∥NF，理由见解析

19、（1）10；60；（2）中位数为21、众数为20；（3）奖励标准应定为21万元，理由见解析

20、（1）C（0，1）．

（2）y=x+1．

（3）P1（4，3），P2（）P3（），P4（）．

21、 (1)见解析;(2)36m².

22、（1）购买一个甲奖品需元，买一个乙奖品需要元；（2）该班级最多可购买个甲奖品.

23、 (1)相等；(2)垂直；(3)见解析.

24、（1）最小值为4.8；（2）这样的点有3个，；；.