


广西来宾市部分中学2022-2023学年数学七年级第二学期期末综合测试模拟试题含答案
展开广西来宾市部分中学2022-2023学年数学七年级第二学期期末综合测试模拟试题
(时间:120分钟 分数:120分)
学校_______ 年级_______ 姓名_______
注意事项
1.考生要认真填写考场号和座位序号。
2.试题所有答案必须填涂或书写在答题卡上,在试卷上作答无效。第一部分必须用2B 铅笔作答;第二部分必须用黑色字迹的签字笔作答。
3.考试结束后,考生须将试卷和答题卡放在桌面上,待监考员收回。
一、选择题(每小题3分,共30分)
1.设a、b是直角三角形的两条直角边,若该三角形的周长为12,斜边长为5,则ab的值是( )
A.6 B.8 C.12 D.24
2.在平面直角坐标系中,点![]() 的位置所在的象限是( )
的位置所在的象限是( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
3.观察下列图形,既是轴对称图形又是中心对称图形的有

A.1个 B.2个 C.3个 D.4个
4.一组数据3,4,4,5,若添加一个数4,则发生变化的统计量是( )
A.平均数 B.众数 C.中位数 D.方差
5.若关于![]() 的不等式组
的不等式组![]() 的整数解共5个,则
的整数解共5个,则![]() 的取值范围是( )
的取值范围是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
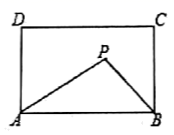
6.如图所示,在矩形![]() 中,
中,![]() ,
,![]() ,矩形内部有一动点
,矩形内部有一动点![]() 满足
满足![]() ,则点
,则点![]() 到
到![]() ,
,![]() 两点的距离之和
两点的距离之和![]() 的最小值为( ).
的最小值为( ).
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
7.用反证法证明命题“若![]() ,则
,则![]() ”时,第一步应假设( )
”时,第一步应假设( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
8.对点Q(0,3)的说法正确的是( )
A.是第一象限的点 B.在![]() 轴的正半轴
轴的正半轴
C.在![]() 轴的正半轴 D.在
轴的正半轴 D.在![]() 轴上
轴上
9.在如图所示的计算程序中,y与x之间的函数关系所对应的图象应为( )
![]()
A.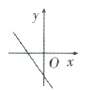 B.
B.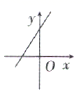 C.
C.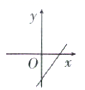 D.
D.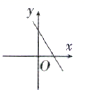
10.在数轴上与原点的距离小于8的点对应的x满足 ( )
A.x<8 B.x>8 C.x<-8或x>8 D.-8<x<8
二、填空题(本大题共有6小题,每小题3分,共18分)
11.一水塘里有鲤鱼、鲢鱼共10000尾,一渔民通过多次捕捞试验后发现,鲤鱼出现的频率为0.36,则水塘有鲢鱼________ 尾.
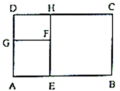
12.下列4种图案中,既是轴对称图形,又是中心对称图形的有__________个.



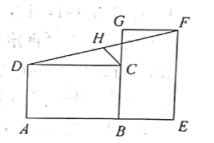
13.如图,矩形![]() 全等于矩形
全等于矩形![]() ,点
,点![]() 在
在![]() 上.连接
上.连接![]() ,点
,点![]() 为
为![]() 的中点.若
的中点.若![]() ,
,![]() ,则
,则![]() 的长为__________.
的长为__________.
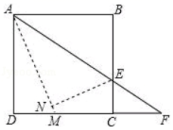
14.如图,正方形ABCD的边长为8,点E是BC上的一点,连接AE并延长交射线DC于点F,将△ABE沿直线AE翻折,点B落在点N处,AN的延长线交DC于点M,当AB=2CF时,则NM的长为_____.
15.如图,在矩形![]() 中,不重叠地放上两张面积分别是
中,不重叠地放上两张面积分别是![]() 和
和![]() 的正方形纸片
的正方形纸片![]() 和
和![]() .矩形
.矩形![]() 没被这两个正方形盖住的面积是________;
没被这两个正方形盖住的面积是________;
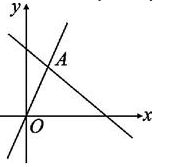
16.如图,函数y=bx和y=ax+4的图象相交于点A(1,3),则不等式bx<ax+4的解集为________.
三、解下列各题(本大题共8小题,共72分)
17.(8分)解答题.
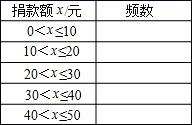
某校学生积极为地震灾区捐款奉献爱心.小颖随机抽查其中30名学生的捐款情况如下:(单位:元)2、5、35、8、5、10、15、20、15、5、45、10、2、8、20、30、40、10、15、15、30、15、8、25、25、30、15、8、10、1.
(1)这30名学生捐款的最大值、最小值、极差、平均数各是多少?
(2)将30名学生捐款额分成下面5组,请你完成频数统计表:
(3)根据上表,作出频数分布直方图.
18.(8分)在平面直角坐标系中,如果点![]() 、点
、点![]() 为某个菱形的一组对角的顶点,且点
为某个菱形的一组对角的顶点,且点![]() 、
、![]() 在直线
在直线![]() 上,那么称该菱形为点
上,那么称该菱形为点![]() 、
、![]() 的“极好菱形”,如图为点
的“极好菱形”,如图为点![]() 、
、![]() 的“极好菱形”的一个示意图.
的“极好菱形”的一个示意图.
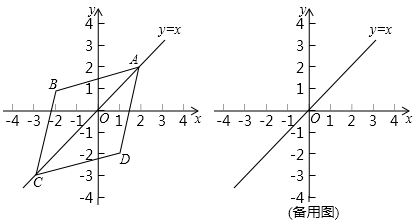
(1)点![]() ,
,![]() ,
,![]() 中,能够成为点
中,能够成为点![]() 、
、![]() 的“极好菱形”的顶点的是_______.
的“极好菱形”的顶点的是_______.
(2)若点![]() 、
、![]() 的“极好菱形”为正方形,则这个正方形另外两个顶点的坐标是________.
的“极好菱形”为正方形,则这个正方形另外两个顶点的坐标是________.
(3)如果四边形![]() 是点
是点![]() 、
、![]() 的“极好菱形”
的“极好菱形”
①当点![]() 的坐标为
的坐标为![]() 时,求四边形
时,求四边形![]() 的面积
的面积
②当四边形![]() 的面积为
的面积为![]() ,且与直线
,且与直线![]() 有公共点时,直接写出
有公共点时,直接写出![]() 的取值范围.
的取值范围.
19.(8分)如图,在正方ABCD中,E是AB边上任一点,BG⊥CE,垂足为O,交AC于点F,交AD于点G.
(1)证明:BE=AG;
(2)E位于什么位置时,∠AEF=∠CEB?说明理由.
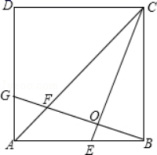
20.(8分)某童装专卖店在销售中发现,一款童装每件进价为80元,销售价为120元时,每天可售出20件,为了迎接“六一”儿童节,商店决定采取适当的降价措施,以扩大销售量增加利润,经市场调查发现,如果每件童装降价1元,那么平均可多售出2件.
(1)每件童装降价多少元时,能更多让利于顾客并且商家平均每天能赢利1200元.
(2)要想平均每天赢利2000元,可能吗?请说明理由.
21.(8分)如图,在□ABCD中,AB=10,AD=8,AC⊥BC,求□ABCD的面积.

22.(10分)如图,在等腰直角三角形ABC中,![]() D是AB的中点,E,F分别是AC,BC.上的点(点E不与端点A,C重合),且
D是AB的中点,E,F分别是AC,BC.上的点(点E不与端点A,C重合),且![]() 连接EF并取EF的中点O,连接DO并延长至点G,使
连接EF并取EF的中点O,连接DO并延长至点G,使![]() ,连接DE,DF,GE,GF
,连接DE,DF,GE,GF
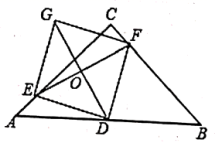
(1)求证:四边形EDFG是正方形;
(2)直接写出当点E在什么位置时,四边形EDFG的面积最小?最小值是多少?
23.(10分)如图,直线AB的函数解析式为y=-2x+8,与x轴交于点A,与y轴交于点B。
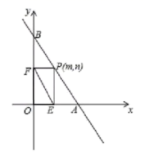
(1)求A、B两点的坐标;
(2)若点P(m,n)为线段AB上的一个动点(与A、B不重合),作PE⊥x轴于点E,PF⊥y轴于点F,连接E,若△PAO的面积为S,求S关于m的函数关系式,并写出m的取值范围。
24.(12分)甲、乙两商场以同样价格出售同样的商品,并且又各自推出不同的优惠方案:在甲商场累计购物超过1元后,超出1元的部分按90%收费;在乙商场累计购物超过50元后,超出50元的部分按95%收费,设小红在同一商场累计购物x元,其中x>1.
(1)根据题题意,填写下表(单位:元)
累计购物实际花费 | 130 | 290 | … | x |
在甲商场 | 127 |
| … |
|
在乙商场 | 126 |
| … |
|
(2)当x取何值时,小红在甲、乙两商场的实际花费相同?
(3)当小红在同一商场累计购物超过1元时,在哪家商场的实际花费少?
参考答案
一、选择题(每小题3分,共30分)
1、C
2、B
3、C
4、D
5、B
6、D
7、C
8、B
9、D
10、D
二、填空题(本大题共有6小题,每小题3分,共18分)
11、1
12、1.
13、![]()
14、![]()
15、![]()
16、x<1
三、解下列各题(本大题共8小题,共72分)
17、 (1) 最大值为1,最小值为2,极差为48,平均数为17.7元.(2)填表见解析;(3)补图见解析.
18、 (1) ![]() ,
,![]() ;
;
(1) (1,3)、(3,1);
(3)①1;②-2≤b≤2.
19、 (1)见解析;(2)当点E位于线段AB中点时,∠AEF=∠CEB ,理由见解析
20、(1)每件童装降价20元时,能更多让利于顾客并且商家平均每天能赢利1200元;(2)不可能,理由详见解析.
21、48
22、(1)详见解析;(2)当点E为线段AC的中点时,四边形EDFG的面积最小,该最小值为4
23、(1)A(4,0),B(0,8);(2)S△PAO=−4m+16(0<m<4);
24、(1)表格见解析;(2)120;(3)当小红累计购物大于120时上没封顶,选择甲商场实际花费少;当小红累计购物超过1元而不到120元时,在乙商场实际花费少.
广西来宾市部分中学2023-2024学年九上数学期末联考试题含答案: 这是一份广西来宾市部分中学2023-2024学年九上数学期末联考试题含答案,共8页。试卷主要包含了考生必须保证答题卡的整洁,给出下列一组数等内容,欢迎下载使用。
广西来宾市部分中学2023-2024学年八年级数学第一学期期末统考模拟试题含答案: 这是一份广西来宾市部分中学2023-2024学年八年级数学第一学期期末统考模拟试题含答案,共7页。试卷主要包含了考生必须保证答题卡的整洁,下列式子为最简二次根式的是,下列计算,正确的是等内容,欢迎下载使用。
广西省来宾市名校2022-2023学年数学七年级第二学期期末综合测试试题含答案: 这是一份广西省来宾市名校2022-2023学年数学七年级第二学期期末综合测试试题含答案,共8页。试卷主要包含了已知直线y=kx-4,下列计算正确的是等内容,欢迎下载使用。












