所属成套资源：人教版数学七年级上册单元检测卷（含答案）
2023年人教版数学七年级上册《整式的加减》单元检测（含答案）
展开
这是一份2023年人教版数学七年级上册《整式的加减》单元检测（含答案），共6页。
2023年人教版数学七年级上册《整式的加减》单元检测一 、选择题1.若数m增加它的x%后得到数n，则n等于( )A.m·x% B.m(1＋x%) C.m＋x% D.m(1＋x)%2.单项式－ab2c3的系数和次数分别是 ( )A.－1、5 B.－1、6 C.1、5 D.1、63.多项式1-x3+x2是( )A.二次三项式 B.三次三项式 C.三次二项式 D.五次三项式4.整式x2-3x的值是4，则3x2-9x＋8的值是( )A.20 B.4 C.16 D.-45.在下列单项式中，与2xy是同类项的是( )A.2x2y2 B.3y C.xy D.4x6.下列各式从左到右的变形中，正确的是( )A.a-(b-c)=a-b-c B.7ab＋6ab=13a2b2 C.a2b-a2b=a2b D.3a2b＋4b2a=7a2b7.在等式1﹣a2＋2ab﹣b2＝1﹣( )中，括号里应填( )A.a2﹣2ab＋b2 B.a2﹣2ab﹣b2C.﹣a2﹣2ab＋b2 D.﹣a2＋2ab﹣b28.化简5(2x﹣3)＋4(3﹣2x)结果为( )A.2x﹣3 B.2x＋9 C.8x﹣3 D.18x﹣39.已知－4xay＋x2yb=－3x2y，则a＋b的值为( )A.1 B.2 C.3 D.410.下列各组代数式中，互为相反数的有（ ）①a－b与－a－b；②a+b与－a－b；③a+1与1－a；④－a+b 与a－b.A.①②④ B.②④ C.①③ D.③④11.甲、乙、丙三家超市为了促销一种定价相同的商品，甲超市先降价20%，后又降价10%；乙超市连续两次降价15%；丙超市一次性降价30%.则顾客到哪家超市购买这种商品更合算( )A.甲 B.乙 C.丙 D.一样12.下列图形都是由同样大小的长方形按一定的规律组成的，其中第①个图形的面积为2cm2，第②个图形的面积为8cm2，第③个图形的面积为18cm2……则第⑩个图形的面积为( )
A.196cm2 B.200cm2 C.216cm2 D.256cm2二 、填空题13.﹣2xy2的次数为 .14.若代数式-4x6y与x2ny是同类项，则常数n的值为_______.15.已知2a﹣3b2=5，则10﹣2a+3b2的值是 .16.多项式xy2﹣9xy＋5x2y﹣25的二次项系数是 .17.{－[－(a＋b)])－{－[－(a－b)])去掉括号得_______.18.下图是某同学一次旅游时在沙滩上用石子摆成的小房子．
观察图形的变化规律，写出第n个小房子用了 块石子．三 、解答题19.化简：2(3a2＋4b)＋3(﹣6a2﹣5b) 20.化简：2(m2＋2n2)﹣3(3m2﹣n2) 21.化简：(8xy﹣x2＋y2)﹣3(﹣x2＋y2＋5xy) 22.化简：﹣3(2x2﹣xy)＋4(x2＋xy﹣6). 23.如图，在一块长为a，宽为2b的长方形铁皮中，以2b为直径分别剪掉两个半圆.(1)求剩下铁皮的面积(用含a，b的式子表示)；(2)当a＝4，b＝1时，求剩下铁皮的面积是多少？(π取3.14)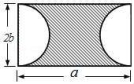
24.阅读下面例题的解题过程，再解答后面的题目.例题：已知代数式9﹣6y﹣4y2＝7，求2y2＋3y＋7的值.解：由9﹣6y﹣4y2＝7得﹣6y﹣4y2＝7﹣9即6y＋4y2＝2，因此2y2＋3y＝1，
所以2y2＋3y＋7＝8.问题：已知代数式14x﹣21x2＝﹣14，求9x2﹣6x﹣5的值. 25.已知a、b、c这三个有理数在数轴上的位置如图所示，化简：|b﹣c|﹣|a﹣b|＋|a＋c|.
26.小明做一道数学题：“已知两个多项式A，B，A=……，B=x2＋3x﹣2，计算2A＋B的值.”小明误把“2A＋B”看成“A＋2B”，求得的结果为5x2﹣2x＋3，请求出2A＋B的正确结果. 27.某服装厂生产一种西装和领带，西装每套定价200元，领带每条定价40元，在促销活动期间，该厂向客户提供了两种优惠方案(客户只能选择其中一种优惠方案)：①买一套西装送一条领带；②西装按原价的9折收费，领带按原价的8折收费.在促销活动期间，某客户要到该服装厂购买x套西装，y条领带(y＞x).(1)该客户选择两种不同的方案所需总费用分别是多少元？(用含x、y的式子表示并化简)(2)若该客户需要购买10套西装，22条领带，则他选择哪种方案更划算？(3)若该客户需要购买15套西装，40条领带，则他选择哪种方案更划算？
答案1.B.2.B3.B.4.A 5.C6.C7.A8.A9.C10.B11.C12.B13.答案为：314.答案为：315.答案为：5.16.答案为：﹣917.答案为：2b18.答案为：(n2＋4n).19.解：原式＝6a2＋8b﹣18a2﹣15b＝﹣12a2﹣7b.20.解：原式＝2m2＋4n2﹣9m2＋3n2＝7n2﹣7m2.21.解：原式＝8xy﹣x2＋y2＋3x2﹣3y2﹣15xy＝2x2﹣2y2﹣7xy.22.解：﹣3(2x2﹣xy)＋4(x2＋xy﹣6)，＝﹣6x2＋3xy＋4x2＋4xy﹣24，＝﹣2x2＋7xy﹣24.23.解：(1)长方形的面积为：a×2b＝2ab，两个半圆的面积为：π×b2＝πb2，∴阴影部分面积为：2ab﹣πb2(2)当a＝4，b＝1时，∴2ab﹣πb2＝2×4×1﹣3.14×1＝4.8624.解：由14x﹣21x2＝﹣14，得到21x2﹣14x＝14，即3x2﹣2x＝2，则原式＝3(3x2﹣2x)﹣5＝6﹣5＝1.25.解：根据数轴上点的位置得：c＜b＜0＜a，且|a|＜|b|＜|c|，∴b﹣c＞0，a﹣b＞0，a＋c＜0，则原式＝b﹣a﹣a＋b﹣a﹣c＝2b﹣3a﹣c.26.解：由题意，得A=(5x2﹣2x＋3)﹣2(x2＋3x﹣2)=5x2﹣2x＋3﹣2x2﹣6x＋4=3x2﹣8x＋7.所以2A＋B=2(3x2﹣8x＋7)＋(x2＋3x﹣2)=6x2﹣16x＋14＋x2＋3x﹣2=7x2﹣13x＋12.27.解：(1)按方案①购买，需付款：200x＋(y﹣x)×40＝(40y＋160x)元；该客户按方案②购买，需付款：200x•90%＋40y•80%＝(180x＋32y)(元)；(2)当x＝10，y＝22时，按方案①购买，需付款：40×22＋160×10＝2480(元)；该客户按方案②购买，需付款：180×10＋32×22＝2504(元)；∵2480＜2504，∴按方案①更划算；(3)当x＝15，y＝40时，按方案①购买，需付款：40×40＋160×15＝4000(元)；该客户按方案②购买，需付款：180×15＋32×40＝3980(元)；∵4000＞3980，∴按方案②更划算.
