


中考数学一轮复习 相似三角形性质与判定 (1)课件
展开1.如图,五线谱是由等距离、等长度的五条平行横线组成的,同一条直线上的三个点A,B,C都在横线上.若线段AB= 3,则线段BC的长是( )
一、平行线分线段成比例
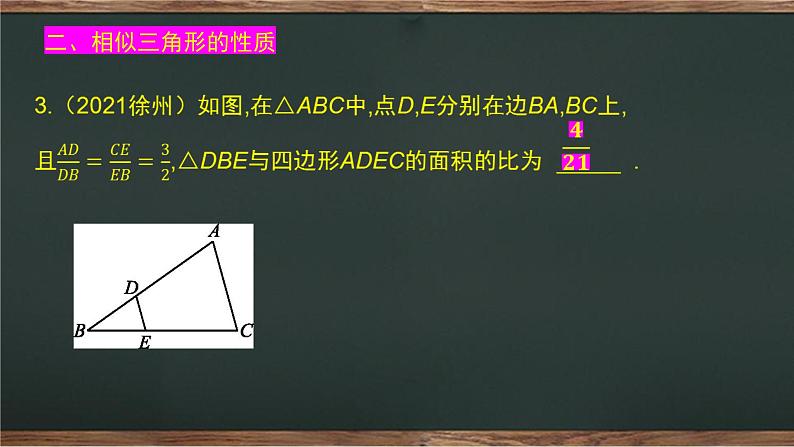
2.如图,l1∥l2∥l3,直线a,b与l1,l2,l3分别相交于点A,B,C和点D,E,F.若AB=3,DE=2,BC=6,则EF= .
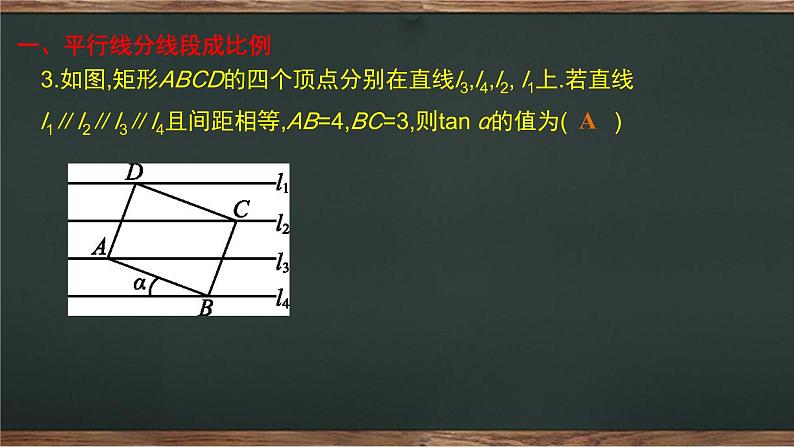
3.如图,矩形ABCD的四个顶点分别在直线l3,l4,l2, l1上.若直线l1∥l2∥l3∥l4且间距相等,AB=4,BC=3,则tan α的值为( )
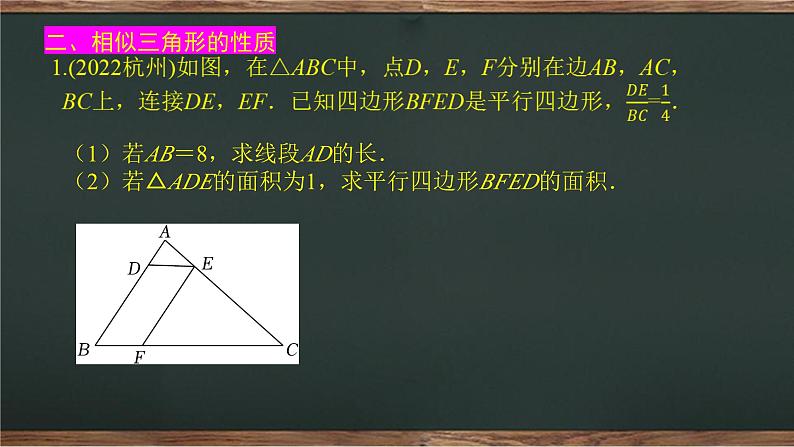
(1)若AB=8,求线段AD的长.(2)若△ADE的面积为1,求平行四边形BFED的面积.
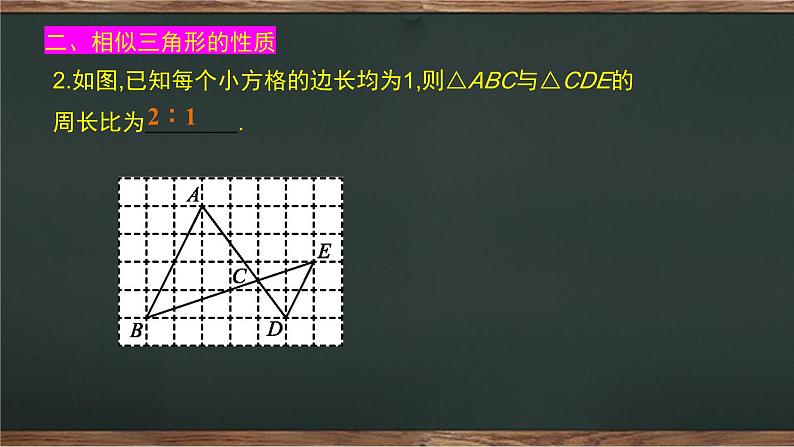
2.如图,已知每个小方格的边长均为1,则△ABC与△CDE的周长比为 .
1.如图,每个小正方形的边长均为1,则下列图形中的三角形(阴影部分)与△A1B1C1相似的是( )
1.(2022•邵阳)如图,在△ABC中,点D在AB边上,点E在AC边上,请添加一个条件 ,使△ADE∽△ABC.
∠ADE=∠B或∠AED=∠C或
2.如图,在△ABC中,点D、E分别在边AB、AC上,下列条件中不能判断△ABC∽△AED的是( )
A.∠AED=∠B B.∠ADE=∠C
A.1对B.2对C.3对D.4对
4.如图,在矩形ABCD中,AB=10,AD=4,点P是边AB上一点,若△APD与△BPC相似,则满足条件的点P有 个.
1.如图,在Rt△ABC中,∠ACB=90°,点D是边AB上的一点,CD⊥AB于D,AD=2,BD=6,则边AC的长为 .
四、相似三角形的判定与性质
D在AC上,且∠APD=∠B,则CD= .
3.(2022•上海)如图所示,在等腰三角形ABC中,AB=AC,点E,F在线段BC上,点Q在线段AB上,且CF=BE,AE2=AQ•AB.求证:(1)∠CAE=∠BAF;(2)CF•FQ=AF•BQ.
4.在正方形网格中,每个小正方形的顶点称为格点,以格点为顶点的三角形叫做格点三角形.如图,△ABC是格点三角形,在图中的6×6正方形网格中作出格点三角形△ADE(不含△ABC),使得△ADE∽△ABC(同一位置的格点三角形△ADE只算一个),这样的格点三角形一共有( )
A.4个B.5个C.6个D.7个
5.(2022•无锡)如图,边长为6的等边三角形ABC内接于⊙O,点D为AC上的动点(点A、C除外),BD的延长线交⊙O于点E,连接CE.(1)求证:△CED∽△BAD;(2)当DC=2AD时,求CE的长.
6.(2021•无锡)如图,四边形ABCD为圆内接四边形,AB=CD,BD平分∠ABC,AC与BD相交于点E.(1)求证:△ABE∽△ACB;(2)若AD=4,BC=6,求线段DE的长度.
7.如图,在Rt△ABC中,∠C=90°,翻折∠C,使点C落在斜边AB上某一点D处,折痕为EF(点E,F分别在边AC, BC上).(1)若△CEF与△ABC相似,①当AC=BC=2时,AD的长为 ; ②当AC=3,BC=4时,AD的长为 . (2)当点D是AB的中点时,△CEF与△ABC相似吗?请说明理由.
8.某数学兴趣小组在数学课外活动中,对多边形内两条互相垂直的线段做了如下探究:
【观察与猜想】(1)如图1,在正方形ABCD中,点E,F分别是AB,AD上的两点,连接DE,CF,DE⊥CF,则 的值为 ;
(2)如图2,在矩形ABCD中,AD=7,CD=4,点E是AD上的一点,连接CE,BD,且CE⊥BD,则
的值为 ;
【类比探究】(3)如图3,在四边形ABCD中,∠A=∠B=90°,点E为AB上一点,连接DE,过点C作DE的垂线交ED的延长线于点G,交AD的延长线于点F,求证:DE•AB=CF•AD;
证明:如图3,过点C作CH⊥AF交 AF的延长线于点H,
数学九年级下册第二十七章 相似27.2 相似三角形27.2.1 相似三角形的判定授课课件ppt: 这是一份数学九年级下册<a href="/sx/tb_c102627_t3/?tag_id=26" target="_blank">第二十七章 相似27.2 相似三角形27.2.1 相似三角形的判定授课课件ppt</a>,共27页。PPT课件主要包含了相似三角形,知识点1,判定三角形相似定理,知识点2,△ADE∽△ABC,基础巩固,综合应用,基本事实,判定定理等内容,欢迎下载使用。
圆的切线性质与判定-中考数学一轮复习课件: 这是一份圆的切线性质与判定-中考数学一轮复习课件,共12页。PPT课件主要包含了复习目标,唯一的公共点,圆的半径,典例分析等内容,欢迎下载使用。
九年级上册3.4 相似三角形的判定与性质一等奖ppt课件: 这是一份九年级上册3.4 相似三角形的判定与性质一等奖ppt课件,共13页。PPT课件主要包含了SAS,ASA,AAS,SSS,复习导入,探究新知,∵DE∥BC,∴DEFC,∴DE∥BC,∴AECE等内容,欢迎下载使用。












