




圆的切线性质与判定-中考数学一轮复习课件
展开一、课标要求 了解切线的概念:探索切线与过切点的半径之间的关系;能判定一条直线是否为圆的切线。会过圆上一点画圆的切线。 二、复习目标 1、复习巩固直线与圆相切的位置关系;2、归纳直线与圆相切的性质和判定方法以及切线长定理,并能运用这些知识进行计算和证明;3、会利用方程思想解决几何问题,体验数形结合思想; 4、在计算与证明中培养学生的分析问题、解决问题以及综合运用知识的能力。
考点梳理1、切线的判定方法:①利用切线的定义:即与圆有______________的直线是圆的切线.②到圆心的距离等于___________的直线是圆的切线.③经过半径的外端点并且__________于这条半径的直线是圆的切线.2、切线的性质:①切线与圆只有_________公共点.②切线到圆心的距离等于圆的______.③切线垂直于经过切点的________.④过圆外一点所画的圆的两条切线,它们的切线长相等。这一点和圆心的连线平分这两条切线的夹角。
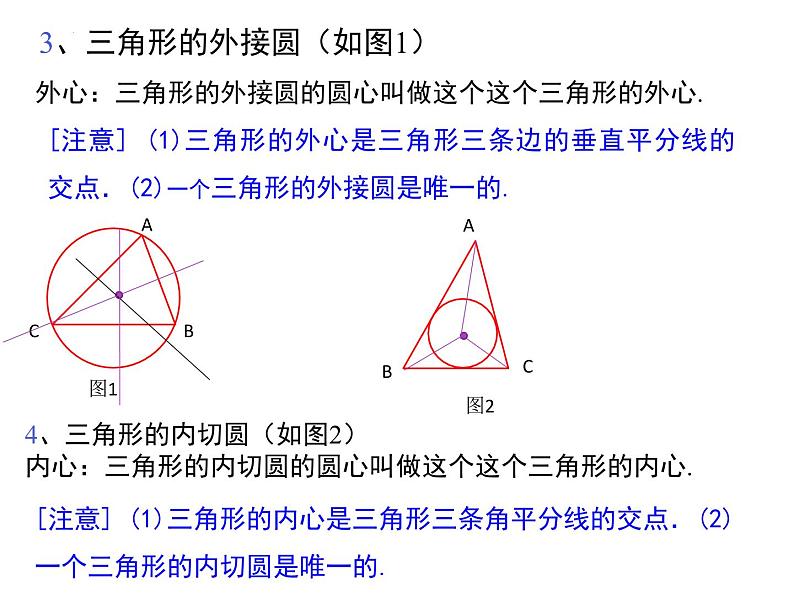
[注意] (1)三角形的内心是三角形三条角平分线的交点.(2)一个三角形的内切圆是唯一的.
[注意] (1)三角形的外心是三角形三条边的垂直平分线的交点.(2)一个三角形的外接圆是唯一的.
圆的切线常用辅助线做法
(1)证切线 时添加辅助线的解题方法有两种: ①有交点,连半径,证垂直; ②无交点,作垂直,证半径;⑵有切线时添加辅助线的解题方法是:见切点,连半径,得垂直;⑶设未知数,通常利用勾股定理或相似建立方程.
(1)利用过圆外一点作圆的两条切线,这两条切线长相等,是解题的基本方法.(2)利用方程思想求切线长常与勾股定理,相似三角形,圆的半径相等紧密相连.
(2019河南中考)如图,在△ABC中,BA=BC,∠ABC=90°,以AB为直径的半圆O交AC于点D,点E是弧BD上不与点B、D重合的任意一点,连结AE交BD于F,连结BE并延长交AC于点G.⑴求证:△ADF≌BDG;⑵填空:若AB=4,且点E是弧BD的中点,则DF的长为__________;取弧AE的中点H,当∠EAB的度数为______时,四边形OBEH为菱形。
(1) 已知半径为2cm的⊙O外一点P,且PO=4cm,PQ切⊙O于Q, 则PQ=________,∠OPQ=_________; (2) ⊿ABC中,∠A=900,AB=AC,以A为圆心的圆切BC于D,若 BC=6cm,则⊙A的半径等于_______;(3) PA,PB都是⊙O的切线A,B是切点.若∠P=480则∠AOB=_____;
4. 如图,以△ABC的边AC为直径的⊙O恰为△ABC的外接圆,∠ABC的平分线交⊙O于点D,过点D作DE∥AC交BC的延长线于点E.(1)求证:DE是⊙O的切线;
5. 如图,已知AB是⊙O的直径,C是⊙O上的点,点D在AB的延长线 上,∠BCD=∠BAC.求证:CD是⊙O的切线.
6. 如图,在△ABC中,O为AC上一点,以点O为圆心,OC为半径作圆,与BC相切于点C,过点A作AD⊥BO的延长线于点D,且∠AOD=∠BAD.求证:AB为⊙O的切线;
初中数学华师大版九年级下册2. 直线和圆的位置关系课前预习ppt课件: 这是一份初中数学华师大版九年级下册2. 直线和圆的位置关系课前预习ppt课件,共12页。PPT课件主要包含了学习目标,重难点,知识回顾,教学过程,探究新知,知识归纳,例题精讲等内容,欢迎下载使用。
中考数学一轮复习 相似三角形性质与判定 (1)课件: 这是一份中考数学一轮复习 相似三角形性质与判定 (1)课件,共24页。PPT课件主要包含了相似三角形的性质,相似三角形的判定等内容,欢迎下载使用。
初中数学人教版九年级上册24.1.1 圆评优课课件ppt: 这是一份初中数学人教版九年级上册24.1.1 圆评优课课件ppt,共18页。PPT课件主要包含了外端点,垂直于,PA与⊙O相切等内容,欢迎下载使用。












