


华师大版七年级上册2 由视图到立体图形精品学案及答案
展开2. 由视图到立体图形
学习目标:
1. 进一步识别物体从三个方向看到的形状图;
2. 能根据三种视图描述基本几何体或实物原形(重点、难点).
自主学习
一、知识链接
1、回忆以下立体图形的三视图,并填空:

① ② ③ ④ ⑤ ⑥ ⑦
主视图是长方形的有 (填序号);
主视图、左视图都是长方形的有 (填序号);
主视图、左视图、俯视图都是长方形的有 (填序号).
合作探究
一、要点探究
探究点1:由视图到立体图形
例1 请根据下图(1)、(2)、(3)的立体图形的三视图说出立体图形的名称.
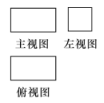
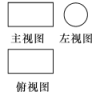
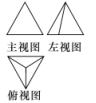
(1) (2) (3)
【针对训练】如图是某几何体的三视图,该几何体是( )

A.圆柱 B.圆锥 C.正三棱柱 D.正三棱锥
例2 某几何体的三视图如图所示,则这个几何体可能是( )
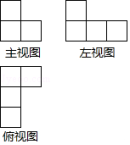 A.
A.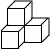 B.
B.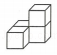
C.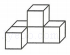 D.
D.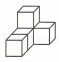
例3 一个几何体的三视图如图所示,则该几何体是( )
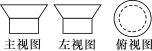
![]()
![]()
![]()
![]()
A B C D
【方法总结】
(1)根据三视图判断物体的形状时,应先综合分析,整体考虑,可以凭借经验大致猜想立体图形的形状,再从细节上去逐一对比、验证,这就要求对常见的立体图形与其三视图非常熟悉;
(2)对一些组合体,在条件允许的情况下,可以借助身边与其形状类似的一些物体按要求组合,通过动手操作来验证自己的猜想,并在多次实践中找出规律.
【针对训练】一个几何体的三视图如图所示,则该几何体是( )
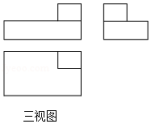 A.
A. B.
B.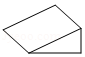
C.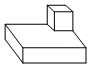 D.
D.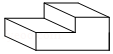
探究点2:由视图到立体图形中的简单计算
例4 如图,是一个几何体的三视图(单位:cm),这个几何体的体积是( )

A.16cm3 B.18cm3 C.22cm3 D.24cm3
【针对训练】某几何体的三视图如图所示,则下列说法错误的是( )
A.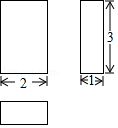 该几何体是长方体
该几何体是长方体
B.该几何体的高是3
C.底面有一边的长是1
D.该几何体的表面积为18平方单位
探究点3:由视图猜测物体的形状
例5 一个几何体由多个完全相同的小正方体组成,它的三视图如图所示,那么组成这个物体的小正方体有( )
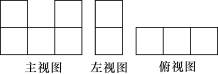
A.2个 B.3个 C.4个 D.5个
【针对训练】1.一个几何体由大小相同的小立方块搭成,从上面看到的几何体形状图如图所示,其中小正方形中的数字表示在该位置的小立方块的个数,则从正面看这个几何体得到的形状图是( )
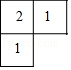
A. B.
B. C.
C.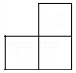 D.
D.
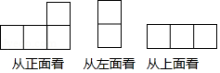
2.如图是由一些相同的小正方体搭成的几何体从三个方向看到的图形,搭成这个几何体的小正方体的个数是 .
二、课堂小结
由三视图描述几何体(或实物原型),一般步骤为:
① 想象:根据各视图想象从各个方向看到的几何体形状;
② 定形:综合确定几何体(或实物原型)的形状;
③ 定大小位置:根据三个视图“长对正,高平齐,宽相等”的关系,确定轮廓线的位置,以及各个方向的尺寸.
当堂检测
1.某立体图形的三视图如图所示,则该立体图形的名称是( )
A.正方体 B.长方体 C.圆柱 D.圆锥
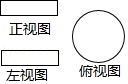
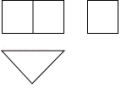
第1 题图 第2题图
2.某几何体的三视图如图所示,则其对应的几何体是( )
A.![]() B.
B. C.
C.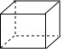 D.
D.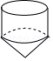
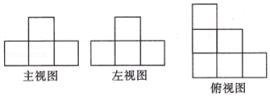
3.如图所示是某个几何体的三视图,与之对应的几何体是( )
A.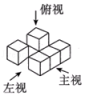 B.
B.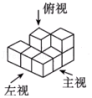 C.
C.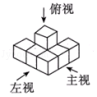 D.
D.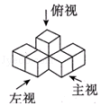
4.如图分别是某校体育运动会的颁奖台和它的主视图,则其俯视图是( )
A.![]() B. C.
B. C.![]() D.
D.
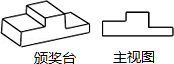
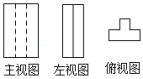
第4题图 第5题图
5.一个几何体的三视图如图所示,则这个几何体是( )
A.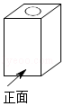 B.
B.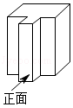 C.
C.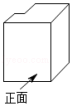 D.
D.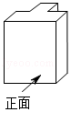
6.下图是一块带有圆形空洞和方形空洞的小木板,则下列物体中既可以堵住圆形空洞,
又可以堵住方形空洞的是 ( )
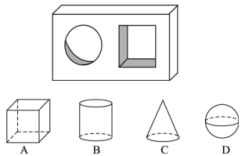
7.由一些相同的小正方体构成的几何体的三视图如图所示,那么构成这个几何体的小正方体有 个.
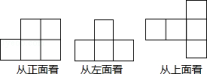
8.如图所示的是某个几何体从三种不同方向所看到的图形.
(1)说出这个几何体的名称;
(2)根据图中有关数据,求这个几何体的表面积.

参考答案
自主学习
一、知识链接
1.(1)①②⑥ (2)①②⑥ (3)②
合作探究
一、要点探究
探究点1:由视图到立体图形
例1
解:(1)是长方体;(2)是圆柱;(3)是三棱锥.
【针对训练】B
例2 D
例3 D 【针对训练】C
探究点2:由视图到立体图形中的简单计算
例4 A 【针对训练】D
探究点3:由视图猜测物体的形状
例5 D 【针对训练】1.B 2.4
当堂检测
1.C 2.B 3.C 4.A 5.D 6.B 7.7
8.(1)根据三视图可得:这个立体图形是三棱柱.
(2)表面积为:![]() ×3×4×2+15×3+15×4+15×5=192.
×3×4×2+15×3+15×4+15×5=192.
初中数学华师大版七年级上册2 垂线优秀学案设计: 这是一份初中数学华师大版七年级上册2 垂线优秀学案设计,共6页。学案主要包含了知识链接,新知预习等内容,欢迎下载使用。
初中数学华师大版七年级上册第3章 整式的加减3.3 整式1 单项式精品学案及答案: 这是一份初中数学华师大版七年级上册第3章 整式的加减3.3 整式1 单项式精品学案及答案,共5页。学案主要包含了要点归纳,方法总结,针对训练等内容,欢迎下载使用。
初中华师大版1 角精品学案及答案: 这是一份初中华师大版1 角精品学案及答案,共6页。学案主要包含了方法总结,易错提醒,针对训练,要点归纳等内容,欢迎下载使用。














