3升4奥数拓展：鸡兔同笼-数学四年级上册人教版

3升4奥数拓展：鸡兔同笼-数学四年级上册人教版

一、选择题

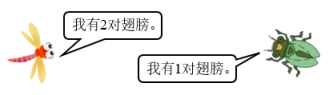
1．蜻蜓和蝉共有32只，翅膀共有44对，蜻蜓有（    ）只。

A．20 B．12 C．24

2．数学竞赛共10道题，做对一题得8分，做错一题（或不做）倒扣5分，小明得41分，他共做错（或不做）了（    ）道题。

A．2 B．3 C．4 D．5

3．爸爸到超市里购买果汁和牛奶一共12瓶，果汁每瓶5元，牛奶每瓶4元，买果汁和牛奶一共花了52元，请问爸爸买了（    ）瓶牛奶。

A．4 B．6 C．8 D．10

4．狮子和孔雀共有25只，有脚76只，孔雀有（    ）只。

A．13只 B．12只 C．10只 D．15只

5．组装车间要装配两轮摩托车和三轮摩托车共21辆，需要51个轮胎，两轮摩托车和三轮摩托车的辆数分别是（    ）。

A．12和9 B．8和13 C．10和11 D．7和14

6．松树上有百灵鸟和松鼠共15只，共48条腿，百灵鸟有（    ）只。

A．9 B．12 C．6

二、填空题

7．鸡兔同笼，有12个头，32只脚，则鸡有(        )，兔有(        )只。

8．自行车和小轿车共10辆，总共有32个轮子。自行车有(        )辆，小轿车有(        )辆。

9．课外活动中，20位同学折纸花122朵，已知男生每人折5朵，女生每人折7朵，男生有(        )人，女生有(        )人。

10．小温购买了三角形与正方形的亚运主题卡片共12张，共41个角。其中三角形卡片有(        )张，正方形卡片有(        )张。

11．有20枚硬币，由1元和5角组成，共16元。那么5角硬币有(        )枚。

12．张经理用A、B两种桌子共10张拼成了一个长26米的展示台（如图），其中A型桌用了(        )张，B型桌用了(        )张。

13．两个小朋友用小棒摆出了数字和，两个数字一共摆了13个，一共用了83根小棒，那么他们摆了(        )个和(        )个。

14．垃圾分类知识竞赛共10道题，每答对一题得3分，答错一题倒扣1分。小明虽然回答了全部的题目，但最后只得了22分。他答错了(        )题。

三、解答题

15．社区为了更好地开展垃圾分类工作，规定：每次正确投放垃圾可获得5个积分，错误投放倒扣3个积分。丽丽家4月份一共投放垃圾20次，获得积分84个，她家这个月正确投放垃圾多少次？

16．钱塘小学“星之队”16人参与“我为钱塘种棵树”活动，男生每人栽4棵树，女生每人栽2棵树，一共栽了52棵树。男女生各有多少人？

17．有鸡和兔共60只，鸡和兔的腿共有140条，问鸡和兔各有几只？

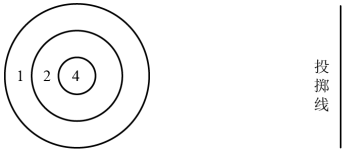
18．在四年级掷准比赛中，小刚共投了8次球，其中有2次投中2分球，其余投中1分球或4分球，总共得分16分，获得第一名。他1分球和4分球各投中几次？

19．一次数学竞赛共有20道题，每做对一道题得5分，做错一题倒扣3分，不做不得分也不扣分，毛毛做了全部题目，正好得76分，问毛毛做对了几道题？

20．四年级一班共有54名学生，体育课上同学们分组跳绳，跳大绳的6人一组，花式跳绳的2人一组，每人只参加其中的一项，正好分成13组，参加跳大绳的和参加花式跳绳的各有多少组？

参考答案：

1．B

【分析】假设32只都是蜻蜓，依此计算出32只蜻蜓的总对数，32只蜻蜓的总对数与实际有翅膀的总对数的差，1只蜻蜓与1只蝉的翅膀的对数差，然后用32只蜻蜓的总对数与实际有翅膀的总对数的差，除以，1只蜻蜓与1只蝉的翅膀的对数差，得到的商就是蝉的只数，最后用蜻蜓和蝉的总只数减蝉的只数即可，依此计算。

【详解】32×2＝64（对）

64－44＝20（对）

2－1＝1（对）

20÷1＝20（只）

32－20＝12（只）

即蜻蜓有12只。

故答案为：B

【点睛】此题考查的是鸡兔同笼问题的计算，应熟练掌握应用假设法解答此类题型。

2．B

【分析】根据题意，假设10道题全做对，则得（分），这样就少得（分）；实际做错一题比做对一题少（分），那么做错的题数（道），据此解答。

【详解】假设全部做对，那么答错（或不做）的题数：

（道）

数学竞赛共10道题，做对一题得8分，做错一题（或不做）倒扣5分，小明得41分，他共做错（或不做）了（3）道题。

故答案为：B

【点睛】此题属于鸡兔同笼问题，解这类题的关键是用假设法进行分析，进而得出结论；也可以用方程进行解答。

3．C

【分析】根据题意，假设全部买的果汁，每瓶5元，共12瓶，用乘法即可求出共有多少元，再用此时的总钱数减去题中给出的52元钱，就是求出比实际多花了多少元，实际每瓶果汁比每瓶牛奶多（5－4）元，然后用除法即可求出牛奶的瓶数，最后再用总个数12减去牛奶的瓶数，就得到果汁的瓶数，据此解答。

【详解】假设全部买的是果汁

（元）

（元）

（元）

牛奶的瓶数：（瓶）

果汁的瓶数：（瓶）

爸爸到超市里购买果汁和牛奶一共12瓶，果汁每瓶5元，牛奶每瓶4元，买果汁和牛奶一共花了52元，请问爸爸买了（8）瓶牛奶。

故答案为：C

【点睛】本题考查鸡兔同笼的问题，找出数量关系，正确计算是解答本题的关键。

4．B

【分析】假设25只全是狮子，则应有25×4＝100只脚，比实际多了100－76＝24只脚，多出来的脚是将孔雀的2只脚看成4只脚来算，每只多算4－2＝2只脚，所以孔雀有24÷2＝12只；据此解答。

【详解】（25×4－76）÷（4－2）

＝（100－76）÷2

＝24÷2

＝12（只）

孔雀有12只。

故答案为：B

【点睛】本题主要考查鸡兔同笼问题，解题时通常采用假设法来解题。

5．A

【分析】设两轮摩托车x辆，则三轮摩托车（21－x）辆，两轮摩托车数量×每辆轮子数＋三轮摩托车数量×每辆轮子数＝51，据此列出方程求出x的值是两轮摩托车数量，总数量－两轮摩托车数量＝三轮摩托车数量。

【详解】解：设两轮摩托车x辆。

2x＋（21－x）×3＝51

2x＋63－3x＝51

63－x＝51

63－x＋x＝51＋x

51＋x＝63

51＋x－51＝63－51

x＝12

21－12＝9（辆）

两轮摩托车和三轮摩托车的辆数分别是12辆、9辆。

故答案为：A

【点睛】用方程解决问题的关键是找到等量关系。

6．C

【分析】假设全是百灵鸟，则应该有腿15×2＝30条，这比已知48条腿少48－30＝18条腿，因为1只松鼠比1只百灵鸟多4－2＝2条腿，由此即可求得松鼠有18÷2＝9只，百灵鸟有15－9＝6只。

【详解】（48－15×2）÷（4－2）

＝（48－30）÷2

＝18÷2

＝9（只）

15－9＝6（只）

则百灵鸟有6只，松鼠有9只。

故答案为：C

【点睛】此题属于典型的鸡兔同笼问题，解答此类题的关键是用假设法进行分析比较，进而得出结论。

7．     8只     4

【分析】假设全部为兔子，共有脚4×12＝48（只），比实际的32只多：48－32＝16（只），因为我们把鸡当成了兔子，每只多算了4－2＝2（只）脚，所以可以算出鸡的只数，列式为：16÷2＝8（只），那么兔子就有：12－8＝4（只）；据此解答。

【详解】根据分析：假设全是兔，则鸡为：

（4×12－32）÷（4－2）

＝（48－32）÷2

＝16÷2

＝8（只）

兔为：12－8＝4（只），所以鸡有8只，兔有4只。

【点睛】本题考查的是“鸡兔同笼”问题的计算方法。

8．     4     6

【分析】假设全是小轿车，则有轮子的个数是10 ×4＝ 40（个），这就与实际的轮子相差了40 －32＝8（个），这是因每辆小轿车比每辆自行车多了4－2＝2（个）轮子，据此可求出自行车的辆数，进而求出小轿车的辆数。

【详解】假设全是小轿车，则自行车有：

（10×4－32）÷（4－2）

＝（40－32）÷2

＝4（辆）

小轿车有：10－4＝6（辆）

【点睛】此题属于鸡兔同笼问题，解题关键是用假设法进行分析，进而得出结论。

9．     9     11

【分析】假设20位都是女同学，依此计算出20位女同学折的总朵数，实际有花的总朵数与20位女同学折的总朵数的差，1位男同学和1位女同学折的朵数差，然后用实际有花的总朵数与20位女同学折的总朵数的差，除以，1位男同学和1位女同学折的朵数差，得到的数就是男生的人数，最后用总人数减男生的人数，即可得到女生的人数。

【详解】7×20＝140（朵）

140－122＝18（朵）

7－5＝2（朵）

18÷2＝9（人）

20－9＝11（人）

即男生有9人，女生有11人。

【点睛】此题考查的是鸡兔同笼问题的计算，应熟练掌握应用假设法解答此类题型。

10．     7     5

【分析】假设全是三角形卡片，则共有的角数是3×12＝36（个），然后与原有的角数相比，少了41－36＝5（个），就是因为三角形卡片比正方形卡片少了（4—3）个角，由此求出正方形卡片的数量，进而求得三角形卡片的数量，据此解答即可

【详解】假设全是三角形卡片，则正方形卡片有：

（41－3×12）÷（4－3）

＝（41－36）÷1

＝5÷1

＝5（张）

12－5＝7（张）

答：三角形卡片有7张，正方形卡片有5张。

【点睛】此题属于典型的鸡兔同笼问题，解答此类题的关键是用假设法进行分析比较，进而得出结论。

11．8

【分析】1元＝10角，假设20枚硬币都是1元的，依此计算出20枚1元硬币的总钱数，1元和5角的钱数差，20枚1元硬币的总钱数与实际总钱数的差，然后用20枚1元硬币的总钱数与实际总钱数的差，除以1元和5角的钱数差，得到的商就是有5角硬币的枚数。

【详解】20×1＝20（元）

20－16＝4（元）

4元＝40角

10－5＝5（角）

40÷5＝8（枚）

5角硬币有8枚。

【点睛】此题考查的是鸡兔同笼问题的计算，应熟练掌握应用假设法解答此类题型。

12．     8     2

【分析】假设10张全是A种桌子，依此计算出10张A种桌子的总长度，展示台的总长度与10张A种桌子的总长度差，1张A型桌子和1张B型桌子的长度差，然后用展示台的总长度与10张A种桌子的总长度差，除以，1张A型桌子和1张B型桌子的长度差，得到的商就是B型桌子的张数，用桌子的总张数减B型桌子的张数，就可得到A型桌子的张数，依此解答。

【详解】假设10张全是A种桌子。

10×3＝30（米）

30－26＝4（米）

3－1＝2（米）

4÷2＝2（张）

10－2＝8（张）

其中A型桌用了8张，B型桌用了2张。

【点睛】此题考查的是鸡兔同笼问题的计算，应熟练掌握应用假设法解答此类题型。

13．     5     8

【分析】摆1个需要7根小棒，摆1个需要6根小棒，假设全是，那么就需要7×13＝91根小棒，比实际多用了91－83＝8根小棒。摆1个比1个多需要7－6＝1根小棒，则摆了8÷1＝8个，就摆了13－8＝5（个）。

【详解】假设全是，则有：

（7×13－83）÷（7－6）

＝（91－83）÷1

＝8÷1

＝8（个）

有13－8＝5（个）

他们摆了5个和8个。

【点睛】此题属于鸡兔同笼问题，解这类题的关键是用假设法进行分析，进而得出结论。

14．2

【分析】假设小明10题全答对，依此计算出10题全答对的总得分，10题全答对的总得分与实际得分的差，答对1题与答错1题的得分差，然后用10题全答对的总得分与实际得分的差，除以答对10题与答错1题的得分差，得到的数就是答错的题数，依此计算。

【详解】10×3＝30（分）

3＋1＝4（分）

30－22＝8（分）

8÷4＝2（题）

他答错了2题。

【点睛】此题考查的是鸡兔同笼问题的计算，应熟练掌握应用假设法解答此类题型。

15．18次

【分析】如果假定全部投放正确，则投放错误的次数＝（总次数×5积分－总积分）÷（每次投放正确和投放错误的差），投放正确的次数＝总次数－投放错误的次数；据此解答。

【详解】（20×5－84）÷（5＋3）

＝（100－84）÷8

＝16÷8

＝2（次）    

20－2＝18（次）

答：她家这个月正确投放垃圾18次。

【点睛】本题考查的是“鸡兔同笼”问题的解答方法。

16．女生有6人，男生有10人

【分析】假设全是男生，那么就栽了16×4＝64（棵）树，比实际多栽了64－52＝12（棵）树。每名男生比女生多栽4－2＝2（棵）树，则女生有12÷2＝6（人），男生就有16－6＝10（人），由此即可解答。

【详解】假设全是男生，则女生有：

（16×4－52）÷（4－2）

＝（64－52）÷2

＝12÷2

＝6（人）

男生有：16－6＝10（人）

答：女生有6人，男生有10人。

【点睛】此题属于鸡兔同笼问题，解这类题的关键是用假设法进行分析，进而得出结论。

17．50只；10只

【分析】一只兔子4条腿，一只鸡2条腿。假设全是兔，则应有（4×60）条腿，实际只有140条。这个差值是因为实际上不全是兔子，每只鸡比兔少2条腿，因此用除法求出假设比实际多的条数里面有多少个2，就是有多少只鸡。用总只数减去鸡的只数就是兔的只数。

【详解】（4×60－140）÷（4－2）

＝（240－140）÷2

＝100÷2

＝50（只） 所以鸡有50只

60－50＝10（只） 所以兔有10只

答：鸡有50只，兔有10只。

【点睛】本题考查鸡兔同笼问题，理解数量关系是解答本题的关键。

18．1分球投了4次，4分球投了2次。

【分析】1分球或4分球一共是得了16－2×2＝12（分），1分球或4分球一共是投了8－2＝6（次），再根据鸡兔同笼原理，假设6次都是4分球来解决。

【详解】16－2×2

＝16－4

＝12（分）

8－2＝6（次）

6×4＝24（分）

24－12＝12（分）

12÷（4－1）

＝12÷3

＝4（次）

6－4＝2（次）

答：1分球投了4次，4分球投了2次。

【点睛】本题的关键在于利用鸡兔同笼的原理来解答，要求同学们要熟练掌握。

19．17道

【分析】做对一道得5分，20道题的总分为20×5＝100（分），毛毛得了76分，100减76可以求出毛毛丢了24分，而做错1道题要丢8分，再用24除以8即可求出做错了几道题，再用20减做错的题数即可解答。

【详解】20×5－76

＝100－76

＝24（分）

24÷（5＋3）

＝24÷8

＝3（道）

20－3＝17（道）

答：毛毛做对了17道题。

【点睛】此题的关键是先求出毛毛丢了几分，据此求出做错的题的数量。

20．跳大绳7组；花式跳绳6组

【分析】如果假定全部是参加跳大绳的，那么参加花式跳绳的人数＝（总组数×跳大绳一组的人数－总人数）÷（每个跳大绳小组和每个花式跳绳小组的人数差），跳大绳小组的人数＝总人数－参加花式跳绳的人数；据此解答。

【详解】假设全是参加跳大绳的，则花式跳绳的人数为：

（13×6－54）÷（6－2）

＝（78－54）÷4

＝24÷4

＝6（组）

参加跳大绳的人数为：13－6＝7（组）

答：参加跳大绳的7组，参加花式跳绳的6组。

【点睛】此题属于鸡兔同笼问题，解这类题的关键是用假设法进行分析，进而得出结论。