广东省肇庆市端州区2022-2023学年数学七下期末学业水平测试试题含答案

广东省肇庆市端州区2022-2023学年数学七下期末学业水平测试试题

（时间：120分钟             分数：120分）

学校_______            年级_______        姓名_______

注意事项

1．考生要认真填写考场号和座位序号。

2．试题所有答案必须填涂或书写在答题卡上，在试卷上作答无效。第一部分必须用2B 铅笔作答；第二部分必须用黑色字迹的签字笔作答。

3．考试结束后，考生须将试卷和答题卡放在桌面上，待监考员收回。

一、选择题(每小题3分,共30分)

1．一家鞋店在一段时间内销售了某种运动鞋50双，各种尺码鞋的销售量如下表所示，你认为商家更应该关注鞋子尺码的(   )

A．平均数 B．中位数 C．众数 D．方差

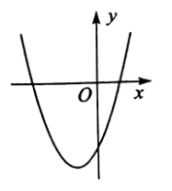
2．在平面直角坐标系中，二次函数的图象如图所示，点，是该二次函数图象上的两点，其中，则下列结论正确的是（   ）

A． B． C．函数的最小值是 D．函数的最小值是

3．下列各式，计算结果正确的是(　　)

A．×＝10 B．＋＝ C．3－＝3 D．÷＝3

4．某同学在体育备考训练期间，参加了七次测试，成绩依次为（单位：分）51，53，56，53，56，58，56，这组数据的众数、中位数分别是（   ）

A．53，53 B．53，56 C．56，53 D．56，56

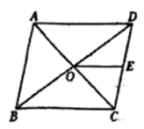
5．如图所示，在平行四边形中，对角线和相交于点，交于点，若，则的长为（    ）

A． B． C． D．

6．如图，以Rt△ABC的三边为直角边分别向外作等腰直角三角形．若AB=5，则图中阴影部分的面积为（　 　）

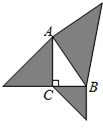
A．6 B． C． D．25

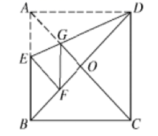
7．如图所示，正方形纸片ABCD中，对角线AC，BD交于点O，折叠正方形纸片ABCD，使AD落在BD上，点A恰好与BD上的点F重合，展开后折痕DE分别交AB，AC于点E，G，连接GF，给出下列结论：

①∠ADG=22.5°；②tan∠AED=2；③S△AGD=S△OGD；④四边形AEFG是菱形；⑤BE=2OG；⑥若S△OGF=1，则正方形ABCD的面积是6+4 ，其中正确的结论个数有（）

A．2个 B．4个 C．3个 D．5个

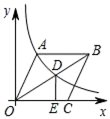
8．如图，在平面直角坐标系中，菱形ABCO的顶点O为坐标原点，边CO在x轴正半轴上，∠AOC＝60°，反比例函数y＝(x＞0)的图象经过点A，交菱形对角线BO于点D，DE⊥x轴于点E，则CE长为(   )

A．1 B． C．2﹣ D．﹣1

9．一个正多边形的每一个外角的度数都是60°，则这个多边形的边数是：（     ）

A．8 B．7 C．6 D．5

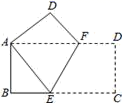
10．如图，将一个边长分别为8，16的矩形纸片ABCD沿EF折叠，使C点与A点重合，则EF与AF的比值为（       ） 

A．4  B． C．2 D．

二、填空题(本大题共有6小题，每小题3分，共18分)

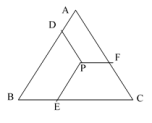
11．如图，已知等边△ABC的边长为10，P是△ABC内一点，PD平行AC，PE平行AD，PF平行BC，点D，E，F分别在AB，BC，AC上，则PD+PE+PF= _______________．

12．已知平行四边形ABCD中，，，AE为BC边上的高，且，则平行四边形ABCD的面积为________．

13．平面直角坐标系中，点关于原点的对称点坐标为______．

14．已知一次函数y=kx+b的图象交y轴于正半轴，且y随x的增大而减小，请写出符合上述条件的一个解析式：_____．

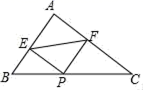
15．如图，在Rt△ABC中，∠A＝90°，AB＝3，AC＝4，P为边BC上一动点，PE⊥AB于E，PE⊥AC于F，则EF的最小值_____．

16．若x-y=，xy=，则代数式（x-1）（y+1）的值等于_____．

三、解下列各题(本大题共8小题，共72分)

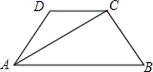
17．（8分）如图，在ABCD中，AB∥CD，AD＝BC，∠B＝60°，AC平分∠DAB．

(1)求∠ACB的度数；

(2)如果AD＝1，请直接写出向量和向量的模．

18．（8分）先化简，再求值：，其中x为不等式组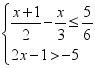的整数解．

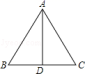
19．（8分）如图，在△ABC中，AB=10，AD平分∠BAC交BC于点D，若AD=8，BD=6，求AC的长．

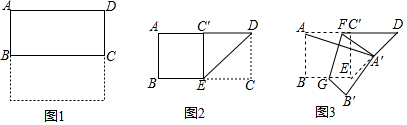
20．（8分）如图1，把一张正方形纸片对折得到长方形ABCD，再沿∠ADC的平分线DE折叠，如图2，点C落在点C′处，最后按图3所示方式折叠，使点A落在DE的中点A′处，折痕是FG，若原正方形纸片的边长为9cm，则FG=_____cm．

21．（8分）某校在一次大课间活动中，采用了四种活动形式：A：跑步；B：跳绳；C：做操；D：游戏，全校学生都选择了一种形式参与活动，小明对同学们选择的活动形式进行了随机抽样调查，并绘制了不完整的两幅统计图，结合统计图，回答下列问题：

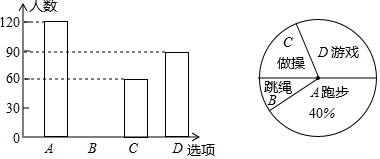
（1）本次调查学生共　   　人，并将条形图补充完整；

（2）如果该校有学生2000人，请你估计该校选择“跑步”这种活动的学生约有多少人？

（3）学校在每班A、B、C、D四种活动形式中，随机抽取两种开展活动，求每班抽取的两种形式恰好是“做操”和“跳绳”的概率．

22．（10分）我省某苹果基地销售优质苹果，该基地对需要送货且购买量在2 000 kg～5 000 kg(含2 000 kg和5 000 kg)的客户有两种销售方案(客户只能选择其中一种方案)：

方案A：每千克5.8元，由基地免费送货；

方案B：每千克5元，客户需支付运费2 000元．

(1)请分别写出按方案A，方案B购买这种苹果的应付款y(元)与购买量x(kg)之间的函数表达式；

(2)求购买量x在什么范围时，选用方案A比方案B付款少；

(3)某水果批发商计划用20 000元，选用这两种方案中的一种，购买尽可能多的这种苹果，请直接写出他应选择哪种方案．

23．（10分）某产品每件成本10元，试销阶段每件产品的销售价x（元）与产品的日销售量y（件）之间的关系如下表

若日销售量y是销售价x的一次函数.

（1）求出日销售量y（件）与销售价x（元）的函数关系式；

（2）求销售价定为30元时，每日的销售利润.

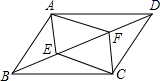
24．（12分）如图，在▱ABCD中，E、F分别是对角线BD上的两点．且BF=DE，求证:AF＝CE.

参考答案

一、选择题(每小题3分,共30分)

1、C

2、D

3、D

4、D

5、B

6、D

7、C

8、C

9、C

10、B

二、填空题(本大题共有6小题，每小题3分，共18分)

11、1

12、2或1

13、

14、

15、2.4

16、2-2

三、解下列各题(本大题共8小题，共72分)

17、 (1)∠ACB＝90°；(1)模分别为1和1．

18、当x=2时，原式=

19、AC=1

20、

21、（1）300；（2）选择“跑步”这种活动的学生约有800人；（3）

22、 (1)方案A：y＝5.8x；方案B：y＝5x＋2 000(2)选用方案A比方案B付款少(3) B

23、（1）一次函数解析式为y=-x+1；（2）每日所获利润为200元.

24、证明见解析.