
2022-2023学年广东省珠海市紫荆中学数学七下期末学业水平测试模拟试题含答案
展开2022-2023学年广东省珠海市紫荆中学数学七下期末学业水平测试模拟试题
(时间:120分钟 分数:120分)
学校_______ 年级_______ 姓名_______
注意事项:
1.答卷前,考生务必将自己的姓名、准考证号、考场号和座位号填写在试题卷和答题卡上。用2B铅笔将试卷类型(B)填涂在答题卡相应位置上。将条形码粘贴在答题卡右上角"条形码粘贴处"。
2.作答选择题时,选出每小题答案后,用2B铅笔把答题卡上对应题目选项的答案信息点涂黑;如需改动,用橡皮擦干净后,再选涂其他答案。答案不能答在试题卷上。
3.非选择题必须用黑色字迹的钢笔或签字笔作答,答案必须写在答题卡各题目指定区域内相应位置上;如需改动,先划掉原来的答案,然后再写上新答案;不准使用铅笔和涂改液。不按以上要求作答无效。
4.考生必须保证答题卡的整洁。考试结束后,请将本试卷和答题卡一并交回。
一、选择题(每小题3分,共30分)
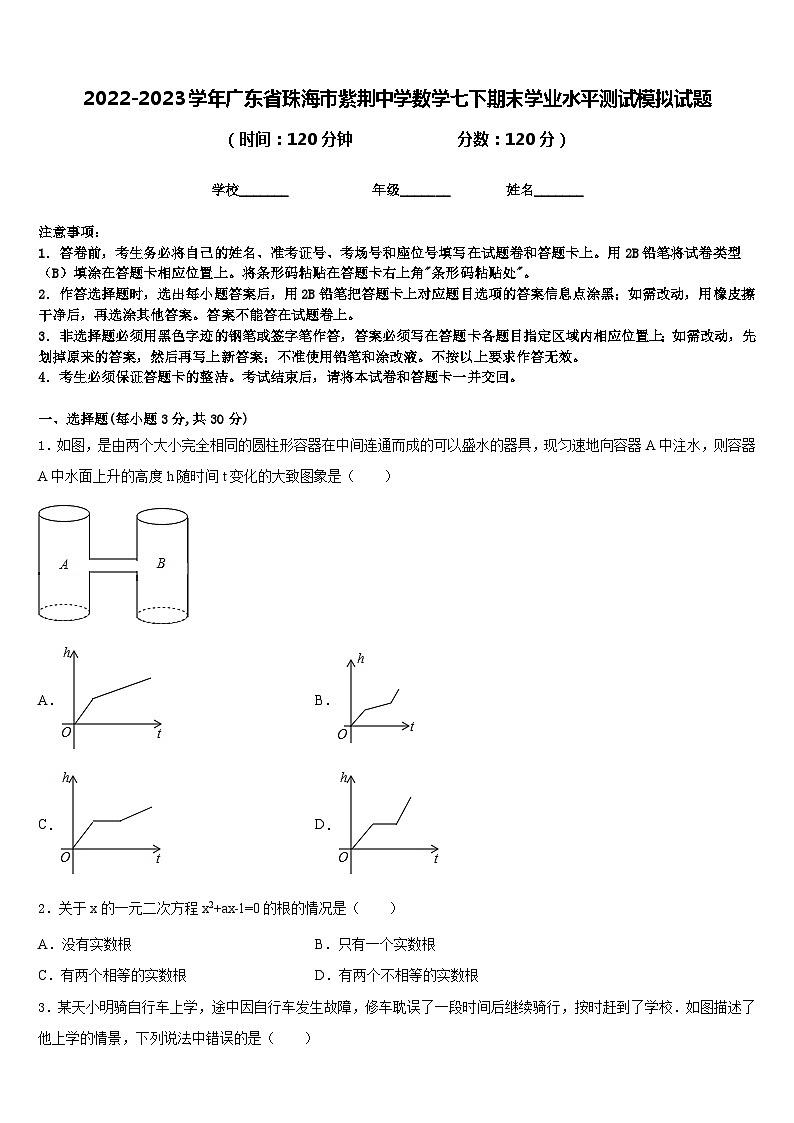
1.如图,是由两个大小完全相同的圆柱形容器在中间连通而成的可以盛水的器具,现匀速地向容器A中注水,则容器A中水面上升的高度h随时间t变化的大致图象是( )
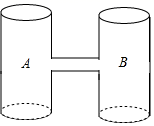
A.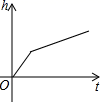 B.
B.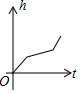
C.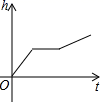 D.
D.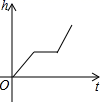
2.关于x的一元二次方程x2+ax﹣1=0的根的情况是( )
A.没有实数根 B.只有一个实数根
C.有两个相等的实数根 D.有两个不相等的实数根
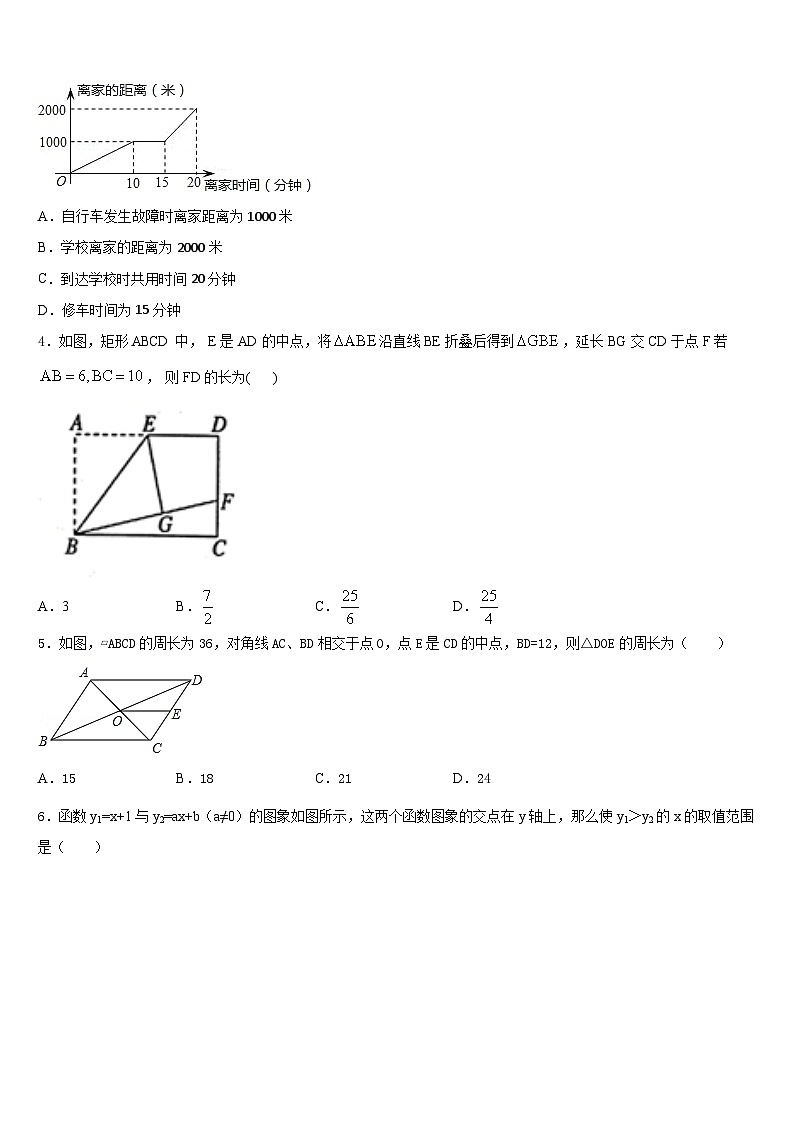
3.某天小明骑自行车上学,途中因自行车发生故障,修车耽误了一段时间后继续骑行,按时赶到了学校.如图描述了他上学的情景,下列说法中错误的是( )
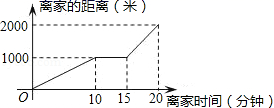
A.自行车发生故障时离家距离为1000米
B.学校离家的距离为2000米
C.到达学校时共用时间20分钟
D.修车时间为15分钟
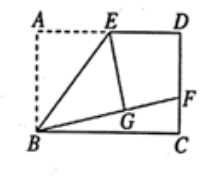
4.如图,矩形ABCD中, E是AD的中点,将![]() 沿直线BE折叠后得到
沿直线BE折叠后得到![]() ,延长BG交CD于点F若
,延长BG交CD于点F若![]() , 则FD的长为( )
, 则FD的长为( )
A.3 B.![]() C.
C.![]() D.
D.![]()
5.如图,▱ABCD的周长为36,对角线AC、BD相交于点O,点E是CD的中点,BD=12,则△DOE的周长为( )
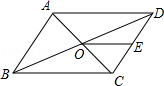
A.15 B.18 C.21 D.24
6.函数y1=x+1与y2=ax+b(a≠0)的图象如图所示,这两个函数图象的交点在y轴上,那么使y1>y2的x的取值范围是( )
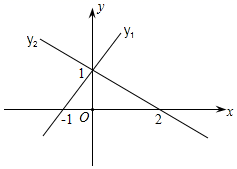
A.x>0 B.x>1 C.x>-1 D.-1<x<2
7.利用反证法证明命题“四边形中至少有一个角是钝角或直角”时,应假设( )
A.四边形中至多有一个内角是钝角或直角
B.四边形中所有内角都是锐角
C.四边形的每一个内角都是钝角或直角
D.四边形中所有内角都是直角
8.如图,已知![]() ,
,![]() 是
是![]() 的角平分线,
的角平分线,![]() ,则点D到
,则点D到![]() 的距离是( )
的距离是( )
A.3 B.4 C.5 D.6
9.某校举办“汉字听写大赛”,7名学生进入决赛,他们所得分数互不相同,比赛共设3个获奖名额,某学生知道自己的分数后,要判断自己能否获奖,他应该关注的统计量是( )
A.平均数 B.中位数 C.众数 D.方差
10.如图,点![]() 在反比例函数
在反比例函数![]() 的图象上,点
的图象上,点![]() 在反比例函数
在反比例函数![]() 的图象上,
的图象上,![]() 轴,连接
轴,连接![]() ,过点
,过点![]() 作
作![]() 轴于点
轴于点![]() ,交
,交![]() 于点
于点![]() ,若
,若![]() ,则
,则![]() 的值为( )
的值为( )
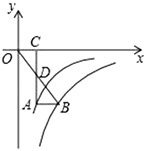
A.﹣4 B.﹣6 C.﹣8 D.﹣9
二、填空题(本大题共有6小题,每小题3分,共18分)
11.中美贸易战以来,强国需更多的中国制造,中芯国际扛起中国芯片大旗,目前我国能制造芯片的最小工艺水平已经达到7纳米,居世界前列,已知1纳米=0.000000001米,用料学记数法将7纳米表示为______米.
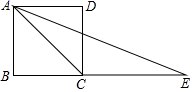
12.如图,在正方形ABCD中,延长BC至E,使CE=CA,则∠E的度数是_____.
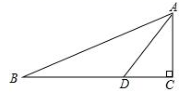
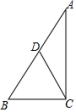
13.如图,![]() 中,
中,![]() D是AB的中点,则CD=__________.
D是AB的中点,则CD=__________.
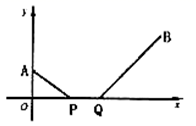
14.如图,在平面直角坐标系中,已知![]() ,
,![]() ,
,![]() 是
是![]() 轴上的一条动线段,且
轴上的一条动线段,且![]() ,当
,当![]() 取最小值时,点
取最小值时,点![]() 坐标为______.
坐标为______.
15.对于平面内任意一个凸四边形ABCD,现从以下四个关系式: ①AB=CD;②AD=BC;③AB∥CD;④∠A=∠C中任取两个作为条件,能够得出这个四边形ABCD是平行四边形的概率是_______.
16.已知直线y=2x+4与x轴、y轴分别交于A、B两点,点P(-1,m)为平面直角坐标系内一动点,若△ABP面积为1,则m的值为______.
三、解下列各题(本大题共8小题,共72分)
17.(8分)物美商场于今年年初以每件25元的进价购进一批商品.当商品售价为40元时,一月份销售256件.二、三月该商品十分畅销.销售量持续走高.在售价不变的基础上,三月底的销售量达到400件.设二、三这两个月月平均增长率不变.
(1)求二、三这两个月的月平均增长率;
(2)从四月份起,商场决定采用降价促销的方式回馈顾客,经调查发现,该商品每降价1元,销售量增加5件,当商品降价多少元时,商场获利4250元?
18.(8分)一次函数![]() 的图象经过
的图象经过![]() 和
和![]() 两点.
两点.
(1)求一次函数的解析式.
(2)当![]() 时,求
时,求![]() 的值.
的值.
19.(8分)如图,在菱形ABCD中,过点D作DE⊥AB于点E,作DF⊥BC于点F,连接EF.求证:(1)△ADE≌△CDF;(2)∠BEF=∠BFE.
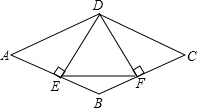
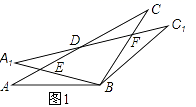
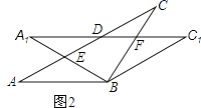
20.(8分)在△ABC中,AB=BC=2,∠ABC=120°,将△ABC绕点B顺时针旋转角α(0°<α<90°)得△A1BC1,A1B交AC于点E,A1C1分别交AC、BC于D、F两点.
(1)如图1,观察并猜想,在旋转过程中,线段BE与BF有怎样的数量关系?并证明你的结论;
(2)如图2,当α=30°时,试判断四边形BC1DA的形状,并说明理由.
21.(8分)先化简![]() ÷
÷![]() ,然后从1、2、3中选取一个你认为合适的数作为a的值代入求值.
,然后从1、2、3中选取一个你认为合适的数作为a的值代入求值.
22.(10分)化简求值:已知![]() ,求
,求![]() 的值.
的值.
23.(10分)甲、乙两座城市的中心火车站A,B两站相距360 km.一列动车与一列特快列车分别从A,B两站同时出发相向而行,动车的平均速度比特快列车快54 km/h,当动车到达B站时,特快列车恰好到达距离A站135 km处的C站.求动车和特快列车的平均速度各是多少?
24.(12分)在平面直角坐标系![]() 中,已知直线
中,已知直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,点
,点![]() 为
为![]() 的中点,点
的中点,点![]() 是线段
是线段![]() 上的动点,四边形
上的动点,四边形![]() 是平行四边形,连接
是平行四边形,连接![]() .设点
.设点![]() 横坐标为
横坐标为![]() .
.
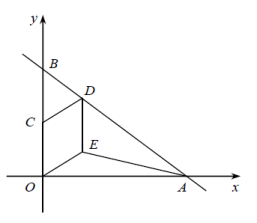
(1)填空:①当![]() ________时,
________时,![]() 是矩形;②当
是矩形;②当![]() ________时,
________时,![]() 是菱形;
是菱形;
(2)当![]() 的面积为
的面积为![]() 时,求点
时,求点![]() 的坐标.
的坐标.
参考答案
一、选择题(每小题3分,共30分)
1、C
2、D
3、D
4、C
5、A
6、A
7、B
8、A
9、B
10、B
二、填空题(本大题共有6小题,每小题3分,共18分)
11、![]()
12、22.5°
13、6.1
14、![]()
15、![]()
16、3或1
三、解下列各题(本大题共8小题,共72分)
17、(1)二、三这两个月的月平均增长率为25%; (2)当商品降价5元时,商品获利4250元.
18、 (1) ![]() ;(2)6.
;(2)6.
19、(1)证明见解析;(2)证明见解析.
20、(1)BE=DF;(2)四边形BC1DA是菱形.
21、![]() , 1.
, 1.
22、![]() ;14
;14
23、特快列车的平均速度为90 km/h,动车的速度为1 km/h.
24、(1)4,![]() ;(2)(1,
;(2)(1,![]() )
)
2023-2024学年广东省珠海市紫荆中学数学九上期末统考模拟试题含答案: 这是一份2023-2024学年广东省珠海市紫荆中学数学九上期末统考模拟试题含答案,共8页。试卷主要包含了考生必须保证答题卡的整洁,抛物线的对称轴是直线,如图,在中,,,,则等于等内容,欢迎下载使用。
2023-2024学年广东省珠海市紫荆中学八上数学期末学业水平测试模拟试题含答案: 这是一份2023-2024学年广东省珠海市紫荆中学八上数学期末学业水平测试模拟试题含答案,共7页。试卷主要包含了有下面的说法,下列说法正确的是,已知,,那么的值是,点M,计算的结果为等内容,欢迎下载使用。
2022-2023学年第二附属中学数学七下期末学业水平测试模拟试题含答案: 这是一份2022-2023学年第二附属中学数学七下期末学业水平测试模拟试题含答案,共6页。试卷主要包含了点关于轴对称的点的坐标是,若,,则代数式的值为等内容,欢迎下载使用。












