


广东省湛江市霞山职业高级中学2022-2023学年七年级数学第二学期期末预测试题含答案
展开广东省湛江市霞山职业高级中学2022-2023学年七年级数学第二学期期末预测试题
(时间:120分钟 分数:120分)
学校_______ 年级_______ 姓名_______
请考生注意:
1.请用2B铅笔将选择题答案涂填在答题纸相应位置上,请用0.5毫米及以上黑色字迹的钢笔或签字笔将主观题的答案写在答题纸相应的答题区内。写在试题卷、草稿纸上均无效。
2.答题前,认真阅读答题纸上的《注意事项》,按规定答题。
一、选择题(每小题3分,共30分)
1.下列命题为真命题的是( )
A.若ab>0,则a>0,b>0
B.两个锐角分别相等的两个直角三角形全等
C.在一个角的内部,到角的两边距离相等的点在这个角的平分线上
D.一组对边平行,另一组对边相等的四边形是平行四边形
2.若顺次连接四边形各边中点所得到的四边形是菱形,则该四边形一定是( )
A.矩形 B.对角线相等的四边形
C.正方形 D.对角线互相垂直的四边形
3.下列不等式的变形中,不正确的是( )
A.若![]() ,则
,则![]() B.若
B.若![]() ,则
,则![]()
C.若![]() ,则
,则![]() D.若
D.若![]() ,则
,则![]()
4.下列方程中,有实数解的方程是( )
A.![]() ; B.
; B.![]() ;
;
C.![]() ; D.
; D.![]()
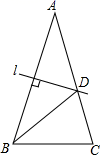
5.如图,在![]() 中,
中,![]() 的垂直平行线交
的垂直平行线交![]() 于
于![]() 点,则
点,则![]() 的度数为( ).
的度数为( ).
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
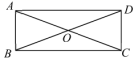
6.在矩形![]() 中,下列结论中正确的是( )
中,下列结论中正确的是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
7.一元二次方程x2-9=0的解为( )
A.x1=x2=3 B.x1=x2=-3 C.x1=3,x2=-3 D.x1=![]() ,x2=-
,x2=-![]()
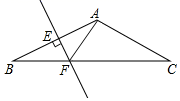
8.如图,在△ABC中,AB=AC,∠BAC=120°,AB的垂直平分线交AB于点E,交BC于点F,连接AF,则∠AFC的度数( )
A.![]()
B.![]()
C.![]()
D.![]()
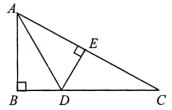
9.如图 ,△ABC 中,∠B=90°,AD 是∠BAC 的平分线,DE⊥AC,垂足为 E,则下列结论中不正确的是( )
A.AB=AE B.BD=DE C.∠ADE=∠CDE D.∠ADB=∠ADE
10.已知 x=-1 是一元二次方程 x2+px+q=0 的一个根,则代数式 p-q 的值是( )
A.1 B.-1 C.2 D.-2
二、填空题(本大题共有6小题,每小题3分,共18分)
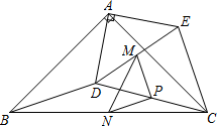
11.如图,△ABC,△ADE均为等腰直角三角形,∠BAC=∠DAE=90°,将△ADE绕点A在平面内自由旋转,连接DC,点M,P,N分别为DE,DC,BC的中点,若AD=3,AB=7,则线段MN的取值范围是______.
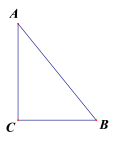
12.如图,![]() 中,
中,![]() ,
,![]() 若动点
若动点![]() 从
从![]() 开始,按C→A→B→C的路径运动(回到点C就停止),且速度为每秒
开始,按C→A→B→C的路径运动(回到点C就停止),且速度为每秒![]() ,则P运动________秒时,
,则P运动________秒时,![]() 为等腰三角形.(提示:直角三角形中,当斜边和一条直角边长分别为
为等腰三角形.(提示:直角三角形中,当斜边和一条直角边长分别为![]() 和
和![]() 时,另一条直角边为
时,另一条直角边为![]() )
)
13.一只不透明的袋子中有1个白球、1个红球和2个黄球,这些球除颜色不同外其它都相同.搅均后从中任意摸出1个球,摸出白球可能性______摸出黄球可能性.(填“等于”或“小于”或“大于”).
14.将直线y=2x-3向上平移5个单位可得______直线.
15.在菱形![]() 中,若
中,若![]() ,
,![]() ,则菱形
,则菱形![]() 的周长为________.
的周长为________.
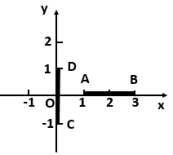
16.如图,已知![]() ,
,![]() ,
,![]() ,
,![]() ,若线段
,若线段![]() 可由线段
可由线段![]() 围绕旋转中心
围绕旋转中心![]() 旋转而得,则旋转中心
旋转而得,则旋转中心![]() 的坐标是______.
的坐标是______.
三、解下列各题(本大题共8小题,共72分)
17.(8分)在坐标系下画出函数![]() 的图象,
的图象,
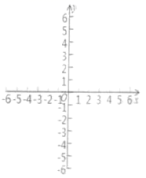
(1)正比例函数![]() 的图象与
的图象与![]() 图象交于A,B两点,A在B的左侧,画出
图象交于A,B两点,A在B的左侧,画出![]() 的图象并求A,B两点坐标
的图象并求A,B两点坐标
(2)根据图象直接写出![]() 时自变量x的取值范围
时自变量x的取值范围
(3)![]() 与x轴交点为C,求
与x轴交点为C,求![]() 的面积
的面积
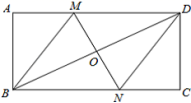
18.(8分)如图,在矩形ABCD中,对角线BD的垂直平分线MN与AD相交于点M,与BC相交于点N.连接BM,DN.
(1)求证:四边形BMDN是菱形;
(2)若AB=4,AD=8,求MD的长.
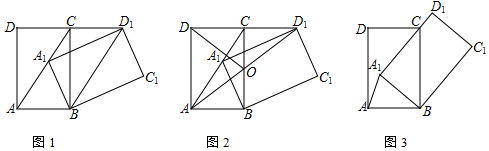
19.(8分)将矩形ABCD绕点B顺时针旋转得到矩形A1BC1D1,点A、C、D的对应点分别为A1、C1、D1
(1)当点A1落在AC上时
①如图1,若∠CAB=60°,求证:四边形ABD1C为平行四边形;
②如图2,AD1交CB于点O.若∠CAB≠60°,求证:DO=AO;
(2)如图3,当A1D1过点C时.若BC=5,CD=3,直接写出A1A的长.
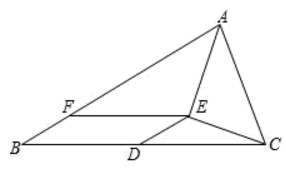
20.(8分)如图,在△ABC中,点D为边BC的中点,点E在△ABC内,AE平分∠BAC,CE⊥AE点F在AB上,且BF=DE
(1)求证:四边形BDEF是平行四边形
(2)线段AB,BF,AC之间具有怎样的数量关系?证明你所得到的结论
21.(8分)如图,已知△ABC中,∠B=90 º,AB=16cm,BC=12cm,P、Q是△ABC边上的两个动点,其中点P从点A开始沿A→B方向运动,且速度为每秒1cm,点Q从点B开始沿B→C→A方向运动,且速度为每秒2cm,它们同时出发,设出发的时间为t秒.
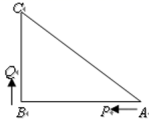
(1)出发2秒后,求PQ的长;
(2)当点Q在边BC上运动时,出发几秒钟后,△PQB能形成等腰三角形?
(3)当点Q在边CA上运动时,求能使△BCQ成为等腰三角形的运动时间.
22.(10分)某地建设一项水利工程,工程需要运送的土石方总量为160万米1.
(1)写出运输公司完成任务所需的时间y(单位:天)与平均每天的工作量x(单位:万米1)之间的函数关系式;
(2)当运输公司平均每天的工作量15万米1,完成任务所需的时间是多少?
(1)为了能在150天内完成任务,平均每天的工作量至少是多少万米1?
23.(10分)(1)解分式方程:![]()
(2)解不等式组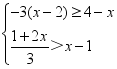 ,并在数轴上表示其解集.
,并在数轴上表示其解集.
24.(12分)已知正方形![]() 与正方形(点C、E、F、G按顺时针排列),是的中点,连接,.
与正方形(点C、E、F、G按顺时针排列),是的中点,连接,.
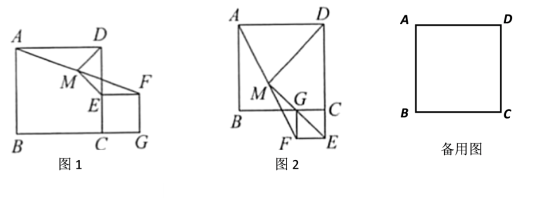
(1)如图1,点![]() 在上,点在的延长线上,
在上,点在的延长线上,
求证:![]() =ME,
=ME,![]() ⊥.ME
⊥.ME
简析: 由是的中点,AD∥EF,不妨延长EM交AD于点N,从而构造出一对全等的三角形,即 ≌ .由全等三角形性质,易证△DNE是 三角形,进而得出结论.
(2)如图2, 在![]() 的延长线上,点在上,(1)中结论是否成立?若成立,请证明你的结论;若不成立,请说明理由.
的延长线上,点在上,(1)中结论是否成立?若成立,请证明你的结论;若不成立,请说明理由.
(3)当AB=5,CE=3时,正方形的顶点C、E、F、G按顺时针排列.若点![]() 在直线CD上,则DM= ;若点E在直线BC上,则DM= .
在直线CD上,则DM= ;若点E在直线BC上,则DM= .
参考答案
一、选择题(每小题3分,共30分)
1、C
2、B
3、D
4、B
5、A
6、C
7、C
8、C
9、C
10、A
二、填空题(本大题共有6小题,每小题3分,共18分)
11、2![]() ≤MN≤5
≤MN≤5![]()
12、3,5.4,6,6.5
13、小于
14、y=1x+1
15、8
16、![]() 或
或![]()
三、解下列各题(本大题共8小题,共72分)
17、(1)图象详见解析,A(![]() ,
,![]() ),B(8,4);(2)x≤
),B(8,4);(2)x≤![]() 或x>8;(3)
或x>8;(3)![]() .
.
18、(1)证明见解析;(2)MD长为1.
19、(1)①证明见解析;②证明见解析;(2)![]()
20、(1)见解析;(2)![]() ,理由见解析
,理由见解析
21、(1)![]() ;(2)
;(2)![]() ;(3)当t为11秒或12秒或13.2秒时,△BCQ为等腰三角形
;(3)当t为11秒或12秒或13.2秒时,△BCQ为等腰三角形
22、(1)![]() ;(2)24天;(1)2.4万米1.
;(2)24天;(1)2.4万米1.
23、(1)原方程无解;(2)x≤1,数轴见解析;
24、(1)等腰直角;(2)结论仍成立,见解析;(3)![]() 或
或![]() ,
,![]() .
.
2022-2023学年广东省湛江市霞山区滨海学校七年级(下)期中数学试卷(含解析): 这是一份2022-2023学年广东省湛江市霞山区滨海学校七年级(下)期中数学试卷(含解析),共15页。试卷主要包含了选择题,填空题,计算题,解答题等内容,欢迎下载使用。
广东省湛江市霞山职业高级中学2023-2024学年数学九上期末检测试题含答案: 这是一份广东省湛江市霞山职业高级中学2023-2024学年数学九上期末检测试题含答案,共7页。试卷主要包含了考生必须保证答题卡的整洁,正五边形的每个外角度数为等内容,欢迎下载使用。
广东省湛江市霞山职业高级中学2023-2024学年八上数学期末预测试题含答案: 这是一份广东省湛江市霞山职业高级中学2023-2024学年八上数学期末预测试题含答案,共7页。试卷主要包含了考生必须保证答题卡的整洁,下列式子,表示4的平方根的是,计算的结果是等内容,欢迎下载使用。












