


广东省梅州市梅江区实验中学2022-2023学年七下数学期末质量跟踪监视模拟试题含答案
展开广东省梅州市梅江区实验中学2022-2023学年七下数学期末质量跟踪监视模拟试题
(时间:120分钟 分数:120分)
学校_______ 年级_______ 姓名_______
请考生注意:
1.请用2B铅笔将选择题答案涂填在答题纸相应位置上,请用0.5毫米及以上黑色字迹的钢笔或签字笔将主观题的答案写在答题纸相应的答题区内。写在试题卷、草稿纸上均无效。
2.答题前,认真阅读答题纸上的《注意事项》,按规定答题。
一、选择题(每小题3分,共30分)
1.用配方法解下列方程,其中应在方程左右两边同时加上4的是( )
A.x2﹣2x=5 B.x2+4x=5 C.2x2﹣4x=5 D.4x2+4x=5
2.如果关于![]() 的分式方程
的分式方程![]() 有非负整数解,且一次函数
有非负整数解,且一次函数![]() 不经过四象限,则所有符合条件的
不经过四象限,则所有符合条件的![]() 的和是( ).
的和是( ).
A.0 B.2 C.3 D.5
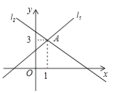
3.如图直线l1:y=ax+b,与直线l2:y=mx+n交于点A(1,3),那么不等式ax+b<mx+n的解集是( )
A.x>3 ![]() B.x<3
B.x<3 ![]() C.x>1
C.x>1 ![]() D.x<1
D.x<1
4.下列命题中,真命题是( )
A.平行四边形的对角线相等 B.矩形的对角线平分对角
C.菱形的对角线互相平分 D.梯形的对角线互相垂直
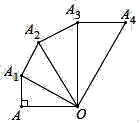
5.如图,OA=![]() ,以OA为直角边作Rt△OAA1,使∠AOA1=30°,再以OA1为直角边作Rt△OA1A2,使∠A1OA2=30°,……,依此法继续作下去,则A1A2的长为( )
,以OA为直角边作Rt△OAA1,使∠AOA1=30°,再以OA1为直角边作Rt△OA1A2,使∠A1OA2=30°,……,依此法继续作下去,则A1A2的长为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
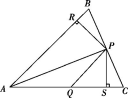
6.如图,在△ABC中,P为BC上一点,PR⊥AB,垂足为R,PS⊥AC,垂足为S,∠CAP=∠APQ,PR=PS,下面的结论:①AS=AR;②QP∥AR;③△BRP≌△CSP.其中正确的是( )
A.①② B.②③ C.①③ D.①②③
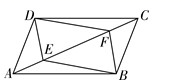
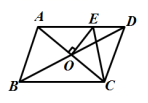
7.如图,点 E,F 是▱ABCD 对角线上两点,在条件①DE=BF;②∠ADE=∠CBF; ③AF=CE;④∠AEB=∠CFD 中,添加一个条件,使四边形 DEBF 是平行四边形,可添加 的条件是( )
A.①②③ B.①②④ C.①③④ D.②③④
8.在一次中学生田径运动会上,参加男子跳高的15名运动员的成绩如表所示:
成绩/米 | 1.50 | 1.60 | 1.65 | 1.70 | 1.75 | 1.80 |
人数 | 2 | 3 | 2 | 3 | 4 | 1 |
则这15运动员的成绩的众数和中位数分别为( )
A.1.75,1.70 B.1.75,1.65 C.1.80,1.70 D.1.80,1.65
9.笔记本每本a元,买3本笔记本共支出y元,在这个问题中:
①a是常量时,y是变量;
②a是变量时,y是常量;
③a是变量时,y也是变量;
④a,y可以都是常量或都是变量.
上述判断正确的有( )
A.1个 B.2个 C.3个 D.4个
10.在□ABCD中,O是AC、BD的交点,过点O 与AC垂直的直线交边AD于点E,若□ABCD的周长为22cm,则△CDE的周长为( ).
A.8cm B.10cm C.11cm D.12cm
二、填空题(本大题共有6小题,每小题3分,共18分)
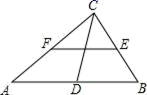
11.如图,在Rt△ABC中,∠ACB=90°,D、E、F分别是AB、BC、CA的中点,若CD=6cm,则EF=_____cm.
12.已知一组数据![]() ,
,![]() ,
,![]() 的方差为4,那么数据
的方差为4,那么数据![]() ,
,![]() ,
,![]() 的方差是___________.
的方差是___________.
13.不等式4x﹣6≥7x﹣15的正整数解的个数是______.
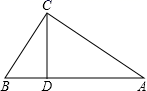
14.已知:如图,△ABC中,∠ACB=90°,AB=5cm,AC=4cm,CD⊥AB于D,求CD的长及三角形的面积.
15.若等腰三角形的两条边长分别为8cm和16cm,则它的周长为_____cm.
16.已知关于![]() 的方程
的方程![]() 的一个解为1,则它的另一个解是__________.
的一个解为1,则它的另一个解是__________.
三、解下列各题(本大题共8小题,共72分)
17.(8分)已知直线y1=2x与直线y2=﹣2x+4相交于点A.以下结论:
①点A的坐标为A(1,2);②当x=1时,两个函数值相等:
③当x<1时,y1<y2; ④直线y1=2x与直线y2=﹣2x+4在平面直角坐标系中的位置关系是平行.其中正确的个数有( )个.
A.4 B.3 C.2 D.1
18.(8分)某社区准备在甲乙两位射箭爱好者中选出一人参加集训,两人各射了5箭,他们的总成绩(单位:环)相同.
| 第1次 | 第2次 | 第3次 | 第4次 | 第5次 |
甲成绩 | 9 | 4 | 7 | 4 | 6 |
乙成绩 | 7 | 5 | 7 | a | 7 |
(1)a=__,![]() =____;
=____;
(2)①分别计算甲、乙成绩的方差.
②请你从平均数和方差的角度分析,谁将被选中.
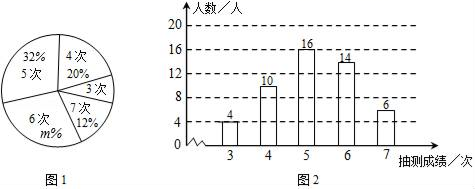
19.(8分)为了解某校九年级男生的体能情况,体育老师随机抽取部分男生进行引体向上测试,并对成绩进行了统计,绘制出如下的统计图①和图②,请跟进相关信息,解答下列问题:
(1)本次抽测的男生人数为 ,图①中m的值为 ;
(2)求本次抽测的这组数据的平均数、众数和中位数;
(3)若规定引体向上5次以上(含5次)为体能达标,根据样本数据,估计该校350名九年级男生中有多少人体能达标.
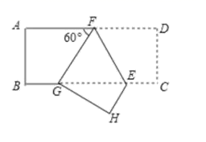
20.(8分)如图,点![]() 、
、![]() 分别在矩形
分别在矩形![]() 的边
的边![]() 、
、![]() 上,把这个矩形沿
上,把这个矩形沿![]() 折叠后,点
折叠后,点![]() 恰好落在
恰好落在![]() 边上的
边上的![]() 点处,且
点处,且![]() .
.
(1)求证:![]() ;
;
(2)连接![]() 、
、![]() ,试证明:
,试证明:![]() .
.
21.(8分)《九章算术》“勾股”章有一题:“今有竹高一丈,末折抵地,去本三尺,问折者几何?”译文为:一根竹子,原来高一丈,虫伤之后,一阵风将竹子折断,其竹梢恰好抵地,抵地处与原竹子底部距离三尺,问原处还有多高的竹子?
请解答上述问题.
22.(10分)树叶有关的问题
如图,一片树叶的长是指沿叶脉方向量出的最长部分的长度(不含叶柄),树叶的宽是指沿与主叶脉垂直方向量出的最宽处的长度,树叶的长宽比是指树叶的长与树叶的宽的比值。
某同学在校园内随机收集了A树、B树、C树三棵的树叶各10片,通过测量得到这些树叶的长y(单位:cm),宽x(单位:cm)的数据,计算长宽比,理如下:
表1 A树、B树、C树树叶的长宽比统计表
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
A树树叶的长宽比 | 4.0 | 4.9 | 5.2 | 4.1 | 5.7 | 8.5 | 7.9 | 6.3 | 7.7 | 7.9 |
B树树叶的长宽比 | 2.5 | 2.4 | 2.2 | 2.3 | 2.0 | 1.9 | 2.3 | 2.0 | 1.9 | 2.0 |
C树树叶的长宽比 | 1.1 | 1.2 | 1.2 | 0.9 | 1.0 | 1.0 | 1.1 | 0.9 | 1.0 | 1.3 |
表1 A树、B树、C树树叶的长宽比的平均数、中位数、众数、方差统计表
| 平均数 | 中位数 | 众数 | 方差 |
A树树叶的长宽比 | 6.2 | 6.0 | 7.9 | 2.5 |
B树树叶的长宽比 | 2.2 |
|
| 0.38 |
C树树叶的长宽比 | 1.1 | 1.1 | 1.0 | 0.02 |
A树、B树、C树树叶的长随变化的情况
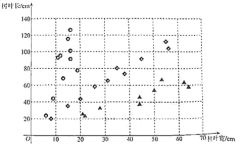
解决下列问题:
(1)将表2补充完整;
(2)①小张同学说:“根据以上信息,我能判断C树树叶的长、宽近似相等。”
②小李同学说:“从树叶的长宽比的平均数来看,我认为,下图的树叶是B树的树叶。”
![]()
请你判断上面两位同学的说法中,谁的说法是合理的,谁的说法是不合理的,并给出你的理由;
(3)现有一片长103cm,宽52cm的树叶,请将该树叶的数用“★”表示在图1中,判断这片树叶更可能来自于A、B、C中的哪棵树?并给出你的理由。
23.(10分)已知x=![]() -1,y=
-1,y=![]() +1,求代数式x2+xy+y2的值.
+1,求代数式x2+xy+y2的值.
24.(12分)边长为![]() ,
,![]() 的矩形发生形变后成为边长为
的矩形发生形变后成为边长为![]() ,
,![]() 的平行四边形,如图1,平行四边形
的平行四边形,如图1,平行四边形![]() 中,
中,![]() ,
,![]() 边上的高为
边上的高为![]() ,我们把
,我们把![]() 与
与![]() 的比值叫做这个平行四边形的“形变比”.
的比值叫做这个平行四边形的“形变比”.
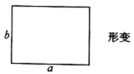
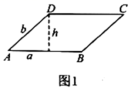
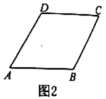
(1)若形变后是菱形![]() (如图2),则形变前是什么图形?
(如图2),则形变前是什么图形?
(2)若图2中菱形![]() 的“形变比”为
的“形变比”为![]() ,求菱形
,求菱形![]() 形变前后的面积之比;
形变前后的面积之比;
(3)当边长为3,4的矩形变后成为一个内角是30°的平行四边形时,求这个平行四边形的“形变比”.
参考答案
一、选择题(每小题3分,共30分)
1、B
2、B
3、D
4、C
5、B
6、A
7、D
8、A
9、B
10、C
二、填空题(本大题共有6小题,每小题3分,共18分)
11、1
12、4
13、3
14、S△ABC=6cm2,CD=![]() cm.
cm.
15、1;
16、![]()
三、解下列各题(本大题共8小题,共72分)
17、B
18、(1)4,6;(2)乙
19、(1)50、1;(2)平均数为5.16次,众数为5次,中位数为5次;(3)估计该校350名九年级男生中有2人体能达标.
20、 (1)见解析;(2)见解析.
21、原处还有4.55尺高的竹子.
22、(1)2.1,2.0;(2)小张同学的说法是合理的,小李学同的说法是不合理;(3)B树;
23、1.
24、(1)正方形;(2)![]() ;(3)
;(3)![]() 或
或![]() .
.
广东省梅州市梅江区实验中学2023-2024学年九年级数学第一学期期末质量跟踪监视试题含答案: 这是一份广东省梅州市梅江区实验中学2023-2024学年九年级数学第一学期期末质量跟踪监视试题含答案,共8页。试卷主要包含了下列四个数中,最小数的是等内容,欢迎下载使用。
广东省梅州市梅江区实验中学2023-2024学年数学八上期末达标检测模拟试题含答案: 这是一份广东省梅州市梅江区实验中学2023-2024学年数学八上期末达标检测模拟试题含答案,共6页。试卷主要包含了答题时请按要求用笔,下列等式正确的是等内容,欢迎下载使用。
西藏拉萨北京实验中学2022-2023学年数学七下期末质量跟踪监视试题含答案: 这是一份西藏拉萨北京实验中学2022-2023学年数学七下期末质量跟踪监视试题含答案,共7页。试卷主要包含了如图,点A在函数y=等内容,欢迎下载使用。












