


山西省乡宁县2022-2023学年数学七年级第二学期期末检测模拟试题含答案
展开山西省乡宁县2022-2023学年数学七年级第二学期期末检测模拟试题
(时间:120分钟 分数:120分)
学校_______ 年级_______ 姓名_______
考生请注意:
1.答题前请将考场、试室号、座位号、考生号、姓名写在试卷密封线内,不得在试卷上作任何标记。
2.第一部分选择题每小题选出答案后,需将答案写在试卷指定的括号内,第二部分非选择题答案写在试卷题目指定的位置上。
3.考生必须保证答题卡的整洁。考试结束后,请将本试卷和答题卡一并交回。
一、选择题:本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.若关于x的方程x2﹣2x+m=0的一个根为﹣1,则另一个根为( )
A.﹣3 B.﹣1 C.1 D.3
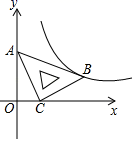
2.在平面直角坐标系xOy中,将一块含有45°角的直角三角板如图放置,直角顶点C的坐标为(1,0),顶点A的坐标为(0,2),顶点B恰好落在第一象限的双曲线上,现将直角三角板沿x轴正方向平移,当顶点A恰好落在该双曲线上时停止运动,则此时点C的对应点C′的坐标为( )
A.(![]() ,0) B.(2,0) C.(
,0) B.(2,0) C.(![]() ,0) D.(3,0)
,0) D.(3,0)
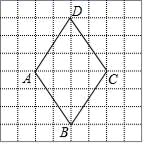
3.如图,边长为1的方格纸中有一四边形ABCD(A,B,C,D四点均为格点),则该四边形的面积为( )
A.4 B.6 C.12 D.24
4.熊大、熊二发现光头强在距离它们300米处伐木,熊二便匀速跑过去阻止,2分钟后熊大以熊二1.2倍的速度跑过去,结果它们同时到达,如果设熊二的速度为x米/分钟,那么可列方程为( ).
A.![]() B.
B.![]()
C.![]() D.
D.![]()
5.荆州古城是闻名遐迩的历史文化名城,“五一”期间相关部门对到荆州观光游客的出行方式进行了随机抽样调查,整理后绘制了两幅统计图(尚不完整).根据图中信息,下列结论错误的是( )
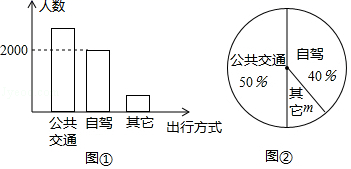
A.本次抽样调查的样本容量是5000
B.扇形图中的m为10%
C.样本中选择公共交通出行的有2500人
D.若“五一”期间到荆州观光的游客有50万人,则选择自驾方式出行的有25万人
6.抛物线![]() 的顶点坐标是( )
的顶点坐标是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
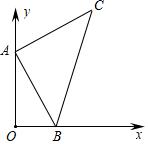
7.如图,已知点A(0,9),点B是x轴正半轴上的一动点,以AB为边作等腰直角三角形ABC使点C在第一象限,∠BAC=90°.设点B的横坐标为x,点C的纵坐标为y则表示y与x的函数关系的图象大致是( )
A.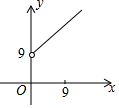 B.
B.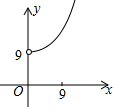
C.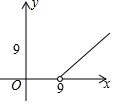 D.
D.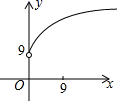
8.如图,在△ABC中,AB=AD=DC,∠B=70°,则∠C的度数为( )
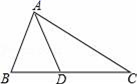
A.35° B.40° C.45° D.50°
9.如图是用程序计算函数值,若输入![]() 的值为3,则输出的函数值
的值为3,则输出的函数值![]() 为( )
为( )
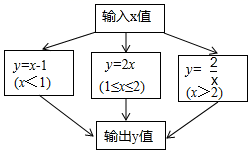
A.2 B.6 C.![]() D.
D.![]()
10.如图, 四边形ABCD的对角线AC,BD相交于点O,E是AB中点,且AE+EO=4,则四边形ABCD的周长为( )
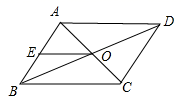
A.32 B.16 C.8 D.4
11.在□ABCD中,∠A:∠B=7:2,则∠C等于( )
A.40° B.80° C.120° D.140°
12.已知二次根式![]() 的值为3,那么
的值为3,那么![]() 的值是( )
的值是( )
A.3 B.9 C.-3 D.3或-3
二、填空题(每题4分,满分20分,将答案填在答题纸上)
13.如图,等腰直角三角形ABC的底边长为6![]() ,AB⊥BC;等腰直角三角形CDE的腰长为2,CD⊥ED;连接AE,F为AE中点,连接FB,G为FB上一动点,则GA的最小值为____.
,AB⊥BC;等腰直角三角形CDE的腰长为2,CD⊥ED;连接AE,F为AE中点,连接FB,G为FB上一动点,则GA的最小值为____.
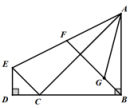
14.如图,在平面直角坐标系中,等边三角形ABC的顶点B,C的坐标分别为(1,0),(3,0),过坐标原点O的一条直线分别与边AB,AC交于点M,N,若OM=MN,则点M的坐标为______________.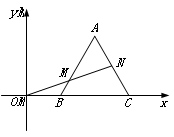
15.现有两根长6分米和3分米的木条,小华想再找一根木条为老师制作一个直角三角形教具,则第三根木条的长度应该为___分米.
16.如图,四边形![]() 中,
中,![]() ,
,![]() ,且
,且![]() ,顺次连接四边形
,顺次连接四边形![]() 各边中点,得到四边形
各边中点,得到四边形![]() ,再顺次连接四边形
,再顺次连接四边形![]() 各边中点得到四边形
各边中点得到四边形![]() ,如此进行下去,得到四边形
,如此进行下去,得到四边形![]() ,则四边形
,则四边形![]() 的面积是________.
的面积是________.
17.在参加“森林重庆”的植树活动中,某班六个绿化小组植树的棵数分别是:10,1,1,10,11,1.则这组数据的众数是____________.
三、解答题 (本大题共7小题,共64分.解答应写出文字说明、证明过程或演算步骤.)
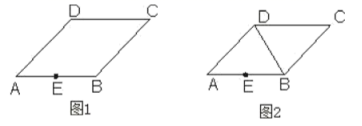
18.(5分)在菱形![]() 中,点
中,点![]() 是边
是边![]() 的中点,试分别在下列两个图形中按要求使用无刻度的直尺画图.
的中点,试分别在下列两个图形中按要求使用无刻度的直尺画图.
(1)在图1中,过点![]() 画
画![]() 的平行线;
的平行线;
(2)在图2中,连接![]() ,在
,在![]() 上找一点
上找一点![]() ,使点
,使点![]() 到点
到点![]() ,
,![]() 的距离之和最短.
的距离之和最短.
19.(5分)在昆明市“创文”工作的带动下,某班学生开展了“文明在行动”的志愿者活动,准备购买一些书包送到希望学校,已知A品牌的书包每个40元,B品牌的书包每个42元,经协商:购买A品牌书包按原价的九折销售;购买B品牌的书包10个以内(包括10个)按原价销售,10个以上超出的部分按原价的八折销售.
(1)设购买x个A品牌书包需要y1元,求出y1关于x的函数关系式;
(2)购买x个B品牌书包需要y2元,求出y2关于x的函数关系式;
(3)若购买书包的数量超过10个,问购买哪种品牌的书包更合算?说明理由.
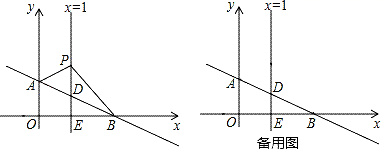
20.(8分)如图,平面直角坐标系中,直线AB交y轴于点A(0,1),交x轴于点B(3,0).直线x=1交AB于点D,交x轴于点E,P是直线x=1上一动点,在点D的上方,设P(1,n).
(1)求直线AB的解析式;
(2)求△ABP的面积(用含n的代数式表示);
(3)当S△ABP=2时,以PB为边在第一象限作等腰直角三角形BPC,求出点C的坐标.
21.(10分)为了倡导节约能源,自某日起,我国对居民用电采用阶梯电价,为了使大多数家庭不增加电费支出,事前就需要了解居民全年月平均用电量的分布情况,制订一个合理的方案.某调查人员随机调查了![]() 市
市![]() 户居民全年月平均用电量(单位:千瓦时)数据如下:
户居民全年月平均用电量(单位:千瓦时)数据如下:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
得到如下频数分布表:
全年月平均用电量/千时 | 频数 | 频率 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
合计 |
|
|
画出频数分布直方图,如下:
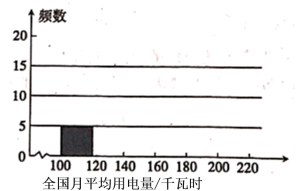
(1)补全数分布表和率分布直方图
(2)若是根据数分布表制成扇形统计图,则不低于![]() 千瓦时的部分圆心角的度数为_____________;
千瓦时的部分圆心角的度数为_____________;
(3)若![]() 市的阶梯电价方案如表所示,你认为这个阶梯电价方案合理吗?
市的阶梯电价方案如表所示,你认为这个阶梯电价方案合理吗?
档次 | 全年月平均用电量/千瓦时 | 电价(元/千瓦时) |
第一档 |
|
|
第二档 |
|
|
第三档 | 大于 |
|
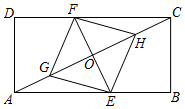
22.(10分)如图,矩形ABCD中,点E,F分别在边AB,CD上,点G,H在对角线AC上,EF与AC相交于点O,AG=CH,BE=DF.
(1)求证:四边形EGFH是平行四边形;
(2)若EG=EH,DC=8,AD=4,求AE的长.
23.(12分)已知,![]() 是等边三角形,
是等边三角形,![]() 是直线
是直线![]() 上一点,以
上一点,以![]() 为顶点做
为顶点做![]() .
. ![]() 交过
交过![]() 且平行于
且平行于![]() 的直线于
的直线于![]() ,求证:
,求证:![]() ;当
;当![]() 为
为![]() 的中点时,(如图1)小明同学很快就证明了结论:他的做法是:取
的中点时,(如图1)小明同学很快就证明了结论:他的做法是:取![]() 的中点
的中点![]() ,连结
,连结![]() ,然后证明
,然后证明![]() . 从而得到
. 从而得到![]() ,我们继续来研究:
,我们继续来研究:
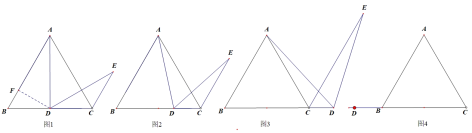
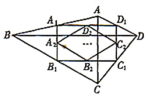
(1)如图2、当D是BC上的任意一点时,求证:![]()
(2)如图3、当D在BC的延长线上时,求证:![]()
(3)当![]() 在
在![]() 的延长线上时,请利用图4画出图形,并说明上面的结论是否成立(不必证明).
的延长线上时,请利用图4画出图形,并说明上面的结论是否成立(不必证明).
参考答案
一、选择题:本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1、D
2、C
3、C
4、C
5、D
6、D
7、A
8、A
9、C
10、B
11、A
12、D
二、填空题(每题4分,满分20分,将答案填在答题纸上)
13、3![]() .
.
14、 (![]() ,
,![]() )
)
15、![]() 或3
或3![]()
16、![]()
17、1
三、解答题 (本大题共7小题,共64分.解答应写出文字说明、证明过程或演算步骤.)
18、(1)详见解析;(2)详见解析.
19、(1)y1=36x;(2)当0≤x≤10时,y2=42x,当x>10时,y2=33.6x+84;(3)若购买35个书包,选A,B品牌都一样,若购买35个以上书包,选B品牌划算,若购买书包个数超过10个但小于35个,选A品牌划算
20、(1)y=![]() x+1;(2)
x+1;(2)![]() ;(3)点C的坐标是(3,4)或(5,2)或(3,2).
;(3)点C的坐标是(3,4)或(5,2)或(3,2).
21、(1)详见解析;(2)144°;(3)合理,理由详见解析.
22、(1)见解析;(2)5.
23、(1)见解析;(2)见解析;(4)见解析,![]() ,仍成立
,仍成立
2023-2024学年山西省乡宁县数学九年级第一学期期末达标检测试题含答案: 这是一份2023-2024学年山西省乡宁县数学九年级第一学期期末达标检测试题含答案,共7页。试卷主要包含了下列事件中必然发生的事件是等内容,欢迎下载使用。
山西省乡宁县2023-2024学年数学八上期末达标检测试题含答案: 这是一份山西省乡宁县2023-2024学年数学八上期末达标检测试题含答案,共7页。试卷主要包含了答题时请按要求用笔,下列图案中不是轴对称图形的是等内容,欢迎下载使用。
山西省孝义市2022-2023学年数学七年级第二学期期末达标检测模拟试题含答案: 这是一份山西省孝义市2022-2023学年数学七年级第二学期期末达标检测模拟试题含答案,共8页。试卷主要包含了已知,下列根式中,不能与合并的是等内容,欢迎下载使用。












