


山西省孝义市2022-2023学年数学七年级第二学期期末达标检测模拟试题含答案
展开山西省孝义市2022-2023学年数学七年级第二学期期末达标检测模拟试题
(时间:120分钟 分数:120分)
学校_______ 年级_______ 姓名_______
注意事项:
1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其它答案标号。回答非选择题时,将答案写在答题卡上,写在本试卷上无效。
3.考试结束后,将本试卷和答题卡一并交回。
一、选择题(每小题3分,共30分)
1.下列命题的逆命题,是假命题的是( )
A.两直线平行,内错角相等 B.全等三角形的对应边相等
C.对顶角相等 D.有一个角为![]() 度的三角形是直角三角形
度的三角形是直角三角形
2.有五组数:①25,7,24;②16,20,12;③9,40,41;④4,6,8;⑤32,42,52,以各组数为边长,能组成直角三角形的个数为( )
A.1 B.2 C.3 D.4
3.下面计算正确的是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
4.已知:在![]() 中,
中,![]() ,求证:
,求证:![]() 若用反证法来证明这个结论,可以假设
若用反证法来证明这个结论,可以假设![]()
![]()
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
5.下列二次根式中,属于最简二次根式的是![]()
![]()
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
6.某班![]() 名男生参加中考体育模拟测试,
名男生参加中考体育模拟测试,![]() 跑步项目成绩如下表:
跑步项目成绩如下表:
成绩(分) |
|
|
|
|
|
|
人数 |
|
|
|
|
|
|
则该班男生成绩的中位数是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
7.用反证法证明命题“在三角形中,至多有一个内角是直角”时,应先假设( )
A.至少有一个内角是直角 B.至少有两个内角是直角
C.至多有一个内角是直角 D.至多有两个内角是直角
8.2018年体育中考中,我班一学习小组6名学生的体育成绩如下表,则这组学生的体育成绩的众数,中位数依次为( )
成绩(分) | 47 | 48 | 50 |
人数 | 2 | 3 | 1 |
A.48,48 B.48,47.5 C.3,2.5 D.3,2
9.为了了解某市八年级女生的体能情况,从某校八年级的甲、乙两班各抽取27名女生进行一分钟跳绳次数的测试,测试数据统计如下:
| 人数 | 中位数 | 平均数 |
甲班 | 27 | 104 | 97 |
乙班 | 27 | 106 | 96 |
如果每分钟跳绳次数大于或等于105为优秀,则甲、乙两班优秀率的大小关系是( )
A.甲优<乙优 B.甲优>乙优 C.甲优=乙优 D.无法比较
10.下列根式中,不能与![]() 合并的是( )
合并的是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
二、填空题(本大题共有6小题,每小题3分,共18分)
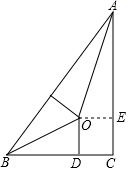
11.我国古代伟大的数学家刘徽将勾股形(古人称直角三角形为勾股形)分割成一个正方形和两对全等的直角三角形,得到一个恒等式.后人借助这种分割方法所得的图形证明了勾股定理,如图所示的就用了这种分割方法,若BD=2,AE=3,则正方形ODCE的边长等于________.
12.将直线![]() 向上平移2个单位得到直线_____________.
向上平移2个单位得到直线_____________.
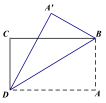
13.如图,把一张长方形的纸沿对角线BD折叠后,顶点A落在A′处,已知∠CDA′=28°,则∠CBD=______________.
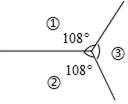
14.如图所示是三个边长相等的正多边形拼成的无缝隙、不重叠的图形的一部分,正多边形①和②的内角都是108°,则正多边形③的边数是______.
15.如图,在矩形![]() 中,
中,![]() ,
,![]() ,点
,点![]() 是
是![]() 边上一点,连接
边上一点,连接![]() ,将
,将![]() 沿
沿![]() 折叠,使点
折叠,使点![]() 落在点
落在点![]() 处.当
处.当![]() 为直角三角形时,
为直角三角形时,![]() __.
__.
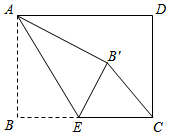
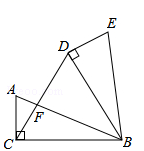
16.如图,在Rt△ABC中,∠ACB=90°,AC=5cm,BC=12cm,将△ABC绕点B顺时针旋转60°,得到△BDE,连接DC交AB于点F,则△ACF与△BDF的周长之和为_______cm.
三、解下列各题(本大题共8小题,共72分)
17.(8分)化简并求值: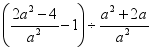 ,其中
,其中![]() .
.
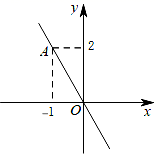
18.(8分)已知:如图,正比例函数y=kx的图象经过点A,
(1)请你求出该正比例函数的解析式;
(2)若这个函数的图象还经过点B(m,m+3),请你求出m的值;
(3)请你判断点P(﹣![]() ,1)是否在这个函数的图象上,为什么?
,1)是否在这个函数的图象上,为什么?
19.(8分)先化简再求值:![]() ,其中
,其中![]() .
.
20.(8分)如图:是某出租车单程收费y(元)与行驶路程x(千米)之间的函数关系图象,根据图象回答下列问题:
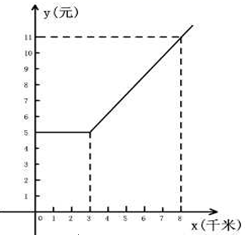
(1)当行使8千米时,收费应为 元;
(2)从图象上你能获得哪些信息?(请写出2条)
① ________
②____________________________
(3)求出收费y(元)与行使x(千米)(x≥3)之间的函数关系式.
21.(8分)请阅读材料,并完成相应的任务.
阿波罗尼奥斯(约公元前262~190年),古希腊数学家,与欧几里得、阿基米德齐名.他的著作《圆锥曲线论》是古代世界光辉的科学成果,可以说是代表了希腊几何的最高水平.阿波罗尼奧斯定理,是欧氏几何的定理,表述三角形三边和中线的长度关系,即三角形任意两边的平方和等于第三边的一半与该边中线的平方和的2倍.
(1)下面是该结论的部分证明过程,请在框内将其补充完整;
已知:如图1所示,在锐角![]() 中,
中,![]() 为中线..
为中线..
求证:![]()
证明:过点![]() 作
作![]() 于点
于点![]()
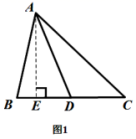
![]() 为中线
为中线
![]()
设![]() ,
,![]() ,
,![]()
![]() ,
,![]()
在![]() 中,
中,![]()
在![]() 中,
中,![]() __________
__________
在![]() 中,
中,![]() __________
__________
![]() __________
__________
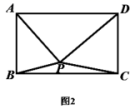
(2)请直接利用阿波罗尼奧斯定理解决下面问题:
如图2,已知点![]() 为矩形
为矩形![]() 内任一点,
内任一点,
求证:![]() (提示:连接
(提示:连接![]() 、
、![]() 交于点
交于点![]() ,连接
,连接![]() )
)
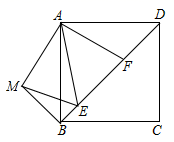
22.(10分)如图,在正方形ABCD中,E、F是对角线BD上两点,将![]() 绕点A顺时针旋转
绕点A顺时针旋转![]() 后,得到
后,得到![]() ,连接EM,AE,且使得
,连接EM,AE,且使得![]() .
.
(1)求证:![]() ;(2)求证:
;(2)求证:![]() .
.
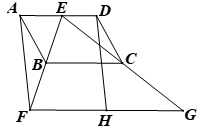
23.(10分)如图,四边形![]() 是平行四边形,
是平行四边形,![]() 为
为![]() 上一点,连接
上一点,连接![]() 并延长,使
并延长,使![]() ,连接
,连接![]() 并延长,使
并延长,使![]() ,连接
,连接![]() ,
,![]() 为
为![]() 的中点,连接
的中点,连接![]() .
.
(1)求证:四边形![]() 是平行四边形;
是平行四边形;
(2)若![]() ,
,![]() ,
,![]() ,求
,求![]() 的度数.
的度数.
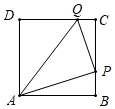
24.(12分)已知,如图,正方形![]() 的边长为4厘米,点
的边长为4厘米,点![]() 从点
从点![]() 出发,经
出发,经![]() 沿正方形的边以2厘米/秒的速度运动;同时,点
沿正方形的边以2厘米/秒的速度运动;同时,点![]() 从点
从点![]() 出发以1厘米/秒的速度沿
出发以1厘米/秒的速度沿![]() 向点
向点![]() 运动,设运动时间为t秒,
运动,设运动时间为t秒,![]() 的面积为
的面积为![]() 平方厘米.
平方厘米.
(1)当![]() 时,
时,![]() 的面积为__________平方厘米;
的面积为__________平方厘米;
(2)求![]() 的长(用含
的长(用含![]() 的代数式表示);
的代数式表示);
(3)当点![]() 在线段
在线段![]() 上运动,且
上运动,且![]() 为等腰三角形时,求此时
为等腰三角形时,求此时![]() 的值;
的值;
(4)求![]() 与
与![]() 之间的函数关系式.
之间的函数关系式.
参考答案
一、选择题(每小题3分,共30分)
1、C
2、C
3、B
4、C
5、A
6、C
7、B
8、A
9、A
10、C
二、填空题(本大题共有6小题,每小题3分,共18分)
11、1
12、![]()
13、31°
14、1.
15、![]() 或1
或1
16、1.
三、解下列各题(本大题共8小题,共72分)
17、![]() ,
,![]()
18、(1)正比例函数解析式为y=﹣2x;(2)m=﹣1;(3)点P不在这个函数图象上,理由见解析.
19、1-![]()
20、(1)11;(2)如:出租车起步价(3千米内)为5元;超出3千米,每千米加收1.2元等;(3)![]() .
.
21、(1)![]() ,
,![]() ,
,![]()
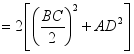 ;(2)见解析
;(2)见解析
22、(1)见解析;(2)见解析.
23、(1)见解析;(2)![]() .
.
24、(1)8;(1)BP=![]() ;(2)
;(2)![]() ;(3)S
;(3)S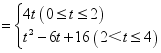 .
.
2023-2024学年山西省孝义市八上数学期末统考模拟试题含答案: 这是一份2023-2024学年山西省孝义市八上数学期末统考模拟试题含答案,共6页。试卷主要包含了证明,下列汉字中是轴对称图形的是,化简的结果为等内容,欢迎下载使用。
2023-2024学年山西省孝义市七年级上学期期中数学质量检测模拟试题(含答案): 这是一份2023-2024学年山西省孝义市七年级上学期期中数学质量检测模拟试题(含答案),共7页。试卷主要包含了中国人很早就开始使用负数,下列说法正确的是,1是2,下列运算结果是正数的是,下列运算正确的是等内容,欢迎下载使用。
山西省(太原临汾地区)2022-2023学年数学七年级第二学期期末达标检测试题含答案: 这是一份山西省(太原临汾地区)2022-2023学年数学七年级第二学期期末达标检测试题含答案,共7页。试卷主要包含了已知,用配方法解方程变形后为等内容,欢迎下载使用。












