


山东省济南历城区六校联考2022-2023学年七下数学期末调研模拟试题含答案
展开山东省济南历城区六校联考2022-2023学年七下数学期末调研模拟试题
(时间:120分钟 分数:120分)
学校_______ 年级_______ 姓名_______
注意事项:
1. 答题前,考生先将自己的姓名、准考证号填写清楚,将条形码准确粘贴在考生信息条形码粘贴区。
2.选择题必须使用2B铅笔填涂;非选择题必须使用0.5毫米黑色字迹的签字笔书写,字体工整、笔迹清楚。
3.请按照题号顺序在各题目的答题区域内作答,超出答题区域书写的答案无效;在草稿纸、试题卷上答题无效。
4.保持卡面清洁,不要折叠,不要弄破、弄皱,不准使用涂改液、修正带、刮纸刀。
一、选择题:本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.12名同学分成甲、乙两队参加播体操比赛,已知每个参赛队有6名队员,他们的身高(单位:cm)如下表所示:
| 队员1 | 队员2 | 队员3 | 队员4 | 队员5 | 队员6 |
甲队 | 176 | 175 | 174 | 172 | 175 | 178 |
乙队 | 170 | 176 | 173 | 174 | 180 | 177 |
设这两队队员平均数依次为![]() ,
,![]() ,身高的方差依次为
,身高的方差依次为![]() ,
,![]() ,则下列关系中,完全正确的是( )
,则下列关系中,完全正确的是( )
A.![]() ,
,![]() B.
B.![]() ,
,![]()
C.![]() ,
,![]() D.
D.![]() ,
,![]()
2.如图,点O是矩形ABCD的对角线AC的中点,M是CD边的中点.若AB=8,OM=3,则线段OB的长为( )
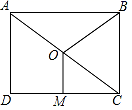
A.5 B.6 C.8 D.10
3.如图,点A、B在反比例函数y=![]() (k>0,x>0)的图象上,过点A、B作x轴的垂线,垂足分别为M,N,延长线段AB交x轴于点C,若OM=MN=NC,S△BNC=2,则k的值为( )
(k>0,x>0)的图象上,过点A、B作x轴的垂线,垂足分别为M,N,延长线段AB交x轴于点C,若OM=MN=NC,S△BNC=2,则k的值为( )
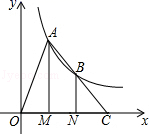
A.4 B.6 C.8 D.12
4.关于圆的性质有以下四个判断:①垂直于弦的直径平分弦,②平分弦的直径垂直于弦,③在同圆或等圆中,相等的弦所对的圆周角相等,④在同圆或等圆中,相等的圆周角所对的弦相等,则四个判断中正确的是( )
A.①③ B.②③ C.①④ D.②④
5.数据3,2,0,1,![]() 的方差等于( )
的方差等于( )
A.0 B.1 C.2 D.3
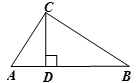
6.如图,△ABC中,CD⊥AB于D,且E是AC的中点.若AD=6,DE=5,则CD的长等于( )
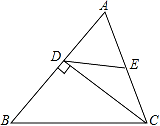
A.7 B.8 C.9 D.10
7.如图,在![]() 中,
中,![]() 的平分线交
的平分线交![]() 于
于![]() ,若
,若![]() ,
,![]() ,则
,则![]() 的长度为( )
的长度为( )
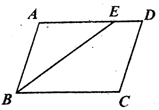
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
8. “龟兔赛跑”是同学们熟悉的寓言故事.如图所示,表示了寓言中的龟、兔的路程S和时间t的关系(其中直线段表示乌龟,折线段表示兔子).下列叙述正确的是( )
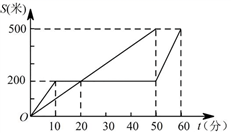
A.赛跑中,兔子共休息了50分钟
B.乌龟在这次比赛中的平均速度是0.1米/分钟
C.兔子比乌龟早到达终点10分钟
D.乌龟追上兔子用了20分钟
9.用配方法解一元二次方程x2-8x+2=0,此方程可化为的正确形式是( ).
A.(x-4)2=14 B.(x-4)2=18 C.(x+4)2=14 D.(x+4)2=18
10.如图,在△ABC中,∠ACB=90°,CD⊥AB,垂足为D,若AC=6,BC=8,则CD等于( )
A.1 B.2 C.3 D.4.8
11.若式子![]() 有意义,则x的取值范围为( ).
有意义,则x的取值范围为( ).
A.x≥2 B.x≠2 C.x≤2 D.x<2
12.如果![]() ,
,![]() 为有理数,那么
为有理数,那么![]() ( )
( )
A.3 B.![]() C.2 D.﹣2
C.2 D.﹣2
二、填空题(每题4分,满分20分,将答案填在答题纸上)
13.一个矩形的长比宽多1cm,面积是![]() ,则矩形的长为___________
,则矩形的长为___________
14.化简分式:![]() =_____.
=_____.
15.如图,依次连接第一个矩形各边的中点得到一个菱形,再依次连接菱形各边的中点得到第二个矩形,按照此方法继续下去.已知第一个矩形的面积为1,则第n个矩形的面积为_____.
![]()
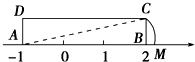
16.如图,矩形![]() 中,
中,![]() ,
,![]() ,
,![]() 在数轴上,若以点
在数轴上,若以点![]() 为圆心,对角线
为圆心,对角线![]() 的长为半径作弧交数轴的正半轴于
的长为半径作弧交数轴的正半轴于![]() ,则点
,则点![]() 的表示的数为_____.
的表示的数为_____.
17.方程![]() 的解是_____.
的解是_____.
三、解答题 (本大题共7小题,共64分.解答应写出文字说明、证明过程或演算步骤.)
18.(5分)某游泳馆普通票价20元/张,暑假为了促销,新推出两种优惠卡:
①金卡售价600元/张,每次凭卡不再收费.
②银卡售价150元/张,每次凭卡另收10元.
暑假普通票正常出售,两种优惠卡仅限暑假使用,不限次数.设游泳x次时,所需总费用为y元.
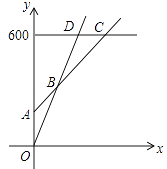
(1)分别写出选择银卡、普通票消费时,y与x之间的函数关系式;
(2)在同一坐标系中,若三种消费方式对应的函数图象如图所示,请求出点A、B、C的坐标;
(3)请根据函数图象,直接写出选择哪种消费方式更合算.
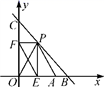
19.(5分)如图,直线y=-x+10与x轴、y轴分别交于点B,C,点A的坐标为(8,0),P(x,y)是直线y=-x+10在第一象限内的一个动点.
(1)求△OPA的面积S与x的函数解析式,并写出自变量x的取值范围;
(2)过点P作PE⊥x轴于点E,作PF⊥y轴于点F,连接EF,是否存在一点P使得EF的长最小,若存在,求出EF的最小值;若不存在,请说明理由.
20.(8分)(1)提出问题:如图1,在正方形![]() 中,点E,H分别在BC,AB上,若
中,点E,H分别在BC,AB上,若![]() 于点O,求证;
于点O,求证;![]() ;
;
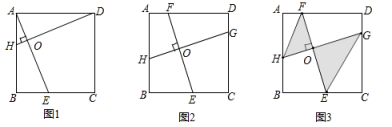
(2)类比探究:如图2,在正方形![]() 中,点B,E,G,F分别在AB,BC,CD,DA上,若
中,点B,E,G,F分别在AB,BC,CD,DA上,若![]() 于点O,探究线段EF与HG的数量关系,并说明理由;
于点O,探究线段EF与HG的数量关系,并说明理由;
(3)综合运用:在(2)问条件下,![]() ,如图3所示,已知
,如图3所示,已知![]() ,
,![]() ,求图中阴影部分的面积。
,求图中阴影部分的面积。
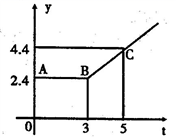
21.(10分)如图所示的折线ABC表示从甲地向乙地打长途电话所需的电话费y(元)与通话时间t(分钟)之间的函数关系的图象.
(1)写出y与t之间的函数关系式;
(2)通话2分钟应付通话费多少元?通话7分钟呢?
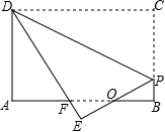
22.(10分)如图,矩形纸片ABCD,AB=4,BC=3,点P在BC边上,将△CDP沿DP折叠,点C落在点E处,PE.、DE分别交AB于点O、F,且OP=OF,则BP的长为______.
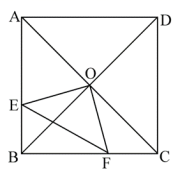
23.(12分)已知:正方形ABCD中,对角线AC、BD交于点O,过O点的两直线OE、OF互相垂直,分别交AB、BC于E、F,连接EF.
(1)求证:OE=OF;
(2)若AE=4,CF=3,求EF的长;
(3)若AB=8cm,请你计算四边形OEBF的面积.
参考答案
一、选择题:本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1、D
2、A
3、C
4、C
5、C
6、B
7、B
8、D
9、A
10、D
11、D
12、A
二、填空题(每题4分,满分20分,将答案填在答题纸上)
13、1
14、-![]()
15、(![]() )n-1
)n-1![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
16、![]()
17、x=﹣1.
三、解答题 (本大题共7小题,共64分.解答应写出文字说明、证明过程或演算步骤.)
18、(1)银卡消费:y=10x+150,普通消费:y=20x;(2)A(0,150),B(15,300),C(45,600);(3)答案见解析.
19、 (1) S=40-4x(0<x<10);(2)存在点P使得EF的长最小,最小值为5![]()
20、(1)见解析;(2)EF=HG,理由见解析;(3)![]() .
.
21、(1)当0<t≤3时,y=2.4;当t>3时,y=t-0.6;(2)2.4元;6.4元
22、![]()
23、(1)见解析;(2)EF=5;(3)16cm2
2023-2024学年山东省济南历城区六校联考九年级数学第一学期期末学业水平测试模拟试题含答案: 这是一份2023-2024学年山东省济南历城区六校联考九年级数学第一学期期末学业水平测试模拟试题含答案,共7页。试卷主要包含了答题时请按要求用笔等内容,欢迎下载使用。
2023-2024学年山东省济南历城区六校联考数学八年级第一学期期末监测试题含答案: 这是一份2023-2024学年山东省济南历城区六校联考数学八年级第一学期期末监测试题含答案,共8页。试卷主要包含了下列四个式子中能因式分解的是等内容,欢迎下载使用。
山东省淄博张店区四校联考2022-2023学年数学七下期末调研模拟试题含答案: 这是一份山东省淄博张店区四校联考2022-2023学年数学七下期末调研模拟试题含答案,共6页。试卷主要包含了若x=1,则x的值是等内容,欢迎下载使用。












