山东省德州市陵城区2022-2023学年数学七下期末统考模拟试题含答案

山东省德州市陵城区2022-2023学年数学七下期末统考模拟试题

（时间：120分钟             分数：120分）

学校_______            年级_______        姓名_______

注意事项

1．考试结束后，请将本试卷和答题卡一并交回．

2．答题前，请务必将自己的姓名、准考证号用0．5毫米黑色墨水的签字笔填写在试卷及答题卡的规定位置．

3．请认真核对监考员在答题卡上所粘贴的条形码上的姓名、准考证号与本人是否相符．

4．作答选择题，必须用2B铅笔将答题卡上对应选项的方框涂满、涂黑；如需改动，请用橡皮擦干净后，再选涂其他答案．作答非选择题，必须用05毫米黑色墨水的签字笔在答题卡上的指定位置作答，在其他位置作答一律无效．

5．如需作图，须用2B铅笔绘、写清楚，线条、符号等须加黑、加粗．

一、选择题(每小题3分,共30分)

1．甲、乙两人在笔直的湖边公路上同起点、同终点、同方向匀速步行2400米，先到终点的人原地休息.已知甲先出发4分钟.在整个步行过程中，甲、乙两人的距离（米）与甲出发的时间（分）之间的关系如图所示，下列结论：①甲步行的速度为60米/分；②乙用16分钟追上甲；③乙走完全程用了30分钟；④乙到达终点时甲离终点还有360米.其中正确的结论有（    ）

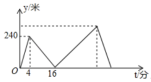
A．1个 B．2个 C．3个 D．4个

2．下列关于一次函数的说法，错误的是(   )

A．图象经过第一、二、四象限

B．随的增大而减小

C．图象与轴交于点

D．当时，

3．如图，在中，是上一点，，，垂足为，是的中点，若，则的长度为（    ）

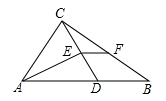
A．36 B．18 C．9 D．5

4．如图，已知小正方形ABCD的面积为1，把它的各边延长一倍得到新正方形；把正方形边长按原法延长一倍得到正方形；以此进行下去，则正方形的面积为　　

A． B． C． D．

5．要使式子有意义，则的取值范围是（ ）

A． B． C． D．

6．某学校组织学生进行社会主义核心价值观的知识竞赛，进入决赛的共有名学生，他们的决赛成绩如下表所示：

那么名学生决赛成绩的众数和中位数分别是（   ）

A．， B．， C．， D．，

7．如图，∠1，∠2，∠3，∠4，∠5是五边形ABCDE的外角，且∠1=∠2=∠3=∠4=75°，则∠AED的度数是（     ）

A．120° B．110° C．115° D．100°

8．解分式方程时，在方程的两边同时乘以（x﹣1）（x+1），把原方程化为x+1+2x（x﹣1）＝2（x﹣1）（x+1），这一变形过程体现的数学思想主要是（　　）

A．类比思想 B．转化思想 C．方程思想 D．函数思想

9．下表是小红填写的实践活动报告的部分内容:

设铁塔顶端到地面的高度为，根据以上条件，可以列出的方程为（  ）

A． B．

C． D．

10．若分式有意义，则x的取值范围是（      ）

A．x=1 B．x≠1 C．x>1 D．x<1

二、填空题(本大题共有6小题，每小题3分，共18分)

11．方程x4﹣16＝0的根是_____．

12．一组数据1，2，3，x，5的平均数是3，则该组数据的方差是_____．

13．若整数m满足，且，则m的值为___________.

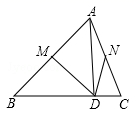
14．如图，在△ABC中，BC=9，AD是BC边上的高，M、N分别是AB、AC边的中点，DM=5，DN=3，则△ABC的周长是__．

15．一般地，在平面直角坐标系中，我们求点到直线间的距离，可用下面的公式求解：

点到直线的距离公式是：

如：求：点到直线的距离．

解：由点到直线的距离公式，得

根据平行线的性质，我们利用点到直线的距离公式，也可以求两平行线间的距离．

则两条平行线：和：间的距离是______．

16．若1＜x＜2，则|x﹣3|+的值为_____．

三、解下列各题(本大题共8小题，共72分)

17．（8分）如图，一次函数的图象与轴、轴分别交于、两点，与反比例函数交于点，过点分别作轴、轴的垂线，垂足分别为点、．若，，．

（1）求点的坐标；

（2）求一次函数和反比例函数的表达式．

18．（8分）（阅读理解）

对于任意正实数、，∵，

∴

∴，只有当时，等号成立．

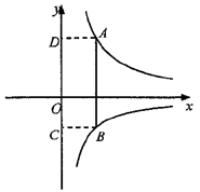
（数学认识）

在（、均为正实数）中，若为定值，则，只有当时，有最小值．

（解决问题）

（1）若时，当_____________时，有最小值为_____________；

（2）如图，已知点在反比例函数的图像上，点在反比例函数的图像上，轴，过点作轴于点，过点作轴于点．求四边形周长的最小值．

19．（8分）甲、乙两车从A城出发匀速行驶至B城，在整个行驶过程中，甲、乙两车离开A城的距离y（千米）与甲车行驶时间x（小时）之间的函数关系如图所示，根据图象提供的信息，解决下列问题：

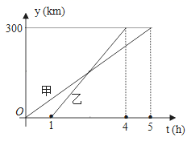
（1）A，B两城相距多少千米？

（2）分别求甲、乙两车离开A城的距离y与x的关系式．

（3）求乙车出发后几小时追上甲车？

（4）求甲车出发几小时的时候，甲、乙两车相距50千米？

20．（8分）某学校计划在总费用2300元的限额内，租用客车送234名学生和6名教师集体外出活动，每辆客车上至少要有1名教师.现有甲、乙两种大客车，它们的载客量和租金如下表所示.

 (1)共需租多少辆客车?

(2)请给出最节省费用的租车方案.

21．（8分）如图，已知一次函数的图象与坐标轴分别交于A、B点，AE平分，交轴于点E．

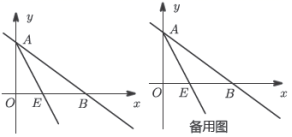
（1）直接写出点A和点B的坐标．

（2）求直线AE的表达式．

（3）过点B作BFAE于点F，过点F分别作FD//OA交AB于点D，FC//AB交轴于点C，判断四边形ACFD的形状并说明理由，求四边形ACFD的面积．

22．（10分）因式分解：．

23．（10分）如图，点O为等边三角形ABC内一点，连接OA，OB，OC，将线段BO绕点B顺时针旋转60°到BM，连接CM，OM．

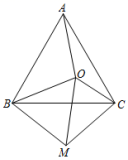
（1）求证：AO＝CM；

（2）若OA＝8，OC＝6，OB＝10，判断△OMC的形状并证明．

24．（12分）平行四边形ABCD中，对角线AC上两点E，F，若AE=CF，四边形DEBF是平行四边形吗？说明你的理由.

参考答案

一、选择题(每小题3分,共30分)

1、C

2、D

3、C

4、B

5、D

6、B

7、A

8、B

9、A

10、B

二、填空题(本大题共有6小题，每小题3分，共18分)

11、±1

12、1

13、，，．

14、1

15、

16、1

三、解下列各题(本大题共8小题，共72分)

17、（1）；（2）.

18、（1）1,1；（1）2.

19、（1）300千米；（2）甲对应的函数解析式为：y＝60x，乙对应的函数解析式为y＝100x−100；（3）1.5 ；（4）小时、1.25小时、3.75小时、小时时，甲、乙两车相距50千米

20、（1）客车总数为6；（1）租4辆甲种客车，1辆乙种客车费用少.

21、（1）A(0,6)，B(8,0)；（2）y=−2x+6；（3）四边形ACFD是菱形，证明见解析；S四边形ACFD=20

22、

23、（1）见解析  （2）直角三角形，证明见解析

24、是，理由见解析.