

四川省都江堰市初2022-2023学年七年级数学第二学期期末质量跟踪监视模拟试题含答案
展开四川省都江堰市初2022-2023学年七年级数学第二学期期末质量跟踪监视模拟试题
(时间:120分钟 分数:120分)
学校_______ 年级_______ 姓名_______
注意事项:
1.答题前,考生先将自己的姓名、准考证号码填写清楚,将条形码准确粘贴在条形码区域内。
2.答题时请按要求用笔。
3.请按照题号顺序在答题卡各题目的答题区域内作答,超出答题区域书写的答案无效;在草稿纸、试卷上答题无效。
4.作图可先使用铅笔画出,确定后必须用黑色字迹的签字笔描黑。
5.保持卡面清洁,不要折暴、不要弄破、弄皱,不准使用涂改液、修正带、刮纸刀。
一、选择题:本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的.
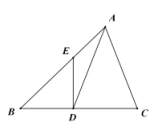
1.如图,在![]() 中,点
中,点![]() 是
是![]() 边上一点,
边上一点,![]() ,过点
,过点![]() 作
作![]() 交
交![]() 于
于![]() ,若
,若![]() 是等腰三角形,则下列判断中正确的是( )
是等腰三角形,则下列判断中正确的是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
2.在四边形ABCD中,对角线AC与BD交于点O,下列各组条件,其中不能判定四边形ABCD是平行四边形的是( )
A.OA=OC,OB=OD B.OA=OC,AB∥CD
C.AB=CD,OA=OC D.∠ADB=∠CBD,∠BAD=∠BCD
3.如图,△ABC以点C为旋转中心,旋转后得到△EDC,已知AB=1.5,BC=4,AC=5,则DE=( )
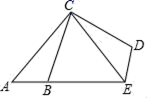
A.1.5 B.3 C.4 D.5
4.如图1,△ABC和△ADE都是等腰直角三角形,∠C和∠ADE都是直角,点C在AE上,△ABC绕着A点经过逆时针旋转后能够与△ADE重合得到图1,再将图1作为“基本图形”绕着A点经过逆时针连续旋转得到图1.两次旋转的角度分别为( )
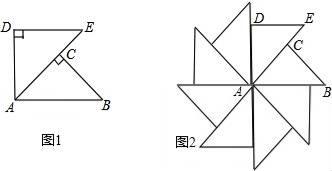
A.45°,90° B.90°,45° C.60°,30° D.30°,60°
5.甲、乙、丙、丁四位选手各10次射击成绩的平均数和方差如下表:
选 手 | 甲 | 乙 | 丙 | 丁 |
平均数(环) | 9.2 | 9.2 | 9.2 | 9.2 |
方差(环2) | 0.035 | 0.015 | 0.025 | 0.027 |
则这四人中成绩发挥最稳定的是( )
A.甲 B.乙 C.丙 D.丁
6.已知点![]() ,
,![]() ,
,![]() 三点都在反比例函数
三点都在反比例函数![]() 的图像上,则下列关系正确的是( ).
的图像上,则下列关系正确的是( ).
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
7.若3x >﹣3y,则下列不等式中一定成立的是( )
A.x>y B.x<y C.x﹣y>0 D.x+y>0
8.某居民小区10户家庭5月份的用水情况统计结果如表所示:这10户家庭的月平均用水量是( )
月用水量/m3 | 4 | 5 | 6 | 8 | 9 |
户数 | 2 | 3 | 3 | 1 | 1 |
A.2m3 ![]() B.3.2m3
B.3.2m3 ![]() C.5.8m3
C.5.8m3 ![]() D.6.4m3
D.6.4m3
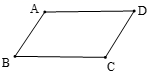
9.如图,是一张平行四边形纸片ABCD,要求利用所学知识作出一个菱形,甲、乙两位同学的作法分别如下:
甲:连接AC,作AC的中垂线交AD、BC于E、F,则四边形AFCE是菱形. |
| 乙:分别作 |
对于甲、乙两人的作法,可判断( )
A.甲正确,乙错误 B.甲错误,乙正确
C.甲、乙均正确 D.甲、乙均错误
10.某农机厂一月份生产零件50万个,第一季度共生产零件182万个.设该厂二、三月份平均每月的增长率为x,那么x满足的方程是( )
A.50(1+x)²=182 B.50+50(1+x)+50(1+x)²=182
C.50(1+2x)=182 D.50+50(1+x)+50(1+2x)²=182
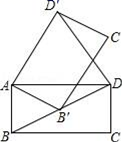
11.如图,在矩形ABCD中,AB=1,BC=![]() .将矩形ABCD绕点A逆时针旋转至矩形AB′C′D′,使得点B′恰好落在对角线BD上,连接DD′,则DD′的长度为( )
.将矩形ABCD绕点A逆时针旋转至矩形AB′C′D′,使得点B′恰好落在对角线BD上,连接DD′,则DD′的长度为( )
A.![]() B.
B.![]() C.
C.![]() +1 D.2
+1 D.2
12.已知不等式mx+n>2的解集是x<0,则下列图中有可能是函数y=mx+n的图象的是( )
A.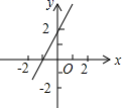 B.
B.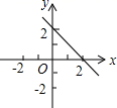 C.
C.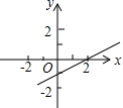 D.
D.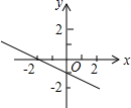
二、填空题(每题4分,满分20分,将答案填在答题纸上)
13.对于平面直角坐标系![]() 中的点
中的点![]() ,给出如下定义:记点
,给出如下定义:记点![]() 到
到![]() 轴的距离为
轴的距离为![]() ,到
,到![]() 轴的距离为
轴的距离为![]() ,若
,若![]() ,则称
,则称![]() 为点
为点![]() 的最大距离;若
的最大距离;若![]() ,则称
,则称![]() 为点
为点![]() 的最大距离.例如:点
的最大距离.例如:点![]() 到到
到到![]() 轴的距离为4,到
轴的距离为4,到![]() 轴的距离为3,因为
轴的距离为3,因为![]() ,所以点
,所以点![]() 的最大距离为4.若点
的最大距离为4.若点![]() 在直线
在直线![]() 上,且点
上,且点![]() 的最大距离为5,则点
的最大距离为5,则点![]() 的坐标是_____.
的坐标是_____.
14.已知关于![]() 的方程
的方程![]() 有解
有解![]() ,则
,则![]() 的值为____________.
的值为____________.
15.如图,在矩形纸片ABCD中,AB=6cm,BC=8cm,将矩形纸片折叠,使点B与点D重合,那么△DCF的周长是___cm.

16.小聪让你写一个含有字母![]() 的二次根式.具体要求是:不论
的二次根式.具体要求是:不论![]() 取何实数,该二次根式都有意义,且二次根式的值为正.你所写的符合要求的一个二次根式是______.
取何实数,该二次根式都有意义,且二次根式的值为正.你所写的符合要求的一个二次根式是______.
17.如果关于x的方程![]() 有实数根,则m的取值范围是_______________.
有实数根,则m的取值范围是_______________.
三、解答题 (本大题共7小题,共64分.解答应写出文字说明、证明过程或演算步骤.)
18.(5分)已知,如图,在△ABC中,D是BC边上的一点,E是AD的中点,过点A作BC的平行线交与BE的延长线于点F,且AF=DC,连结CF.
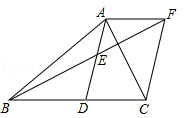
(1)求证:四边形ADCF是平行四边形;
(2)当AB与AC有何数量关系时,四边形ADCF为矩形,请说明理由.
19.(5分)综合与探究
问题情境:
在综合实践课上,李老师让同学们根据如下问题情境,写出两个数学结论:如图(1),正方形ABCD的对角线交于点O,点O又是正方形OEFG的一个顶点(正方形OEFG的边长足够长),将正方形OEFG绕点O做旋转实验,OE与BC交于点M,OG与DC交于点N.

“兴趣小组”写出的两个数学结论是:
①S△OMC+S△ONC=![]() S正方形ABCD;
S正方形ABCD;
②BM1+CM1=1OM1.
问题解决:
(1)请你证明“兴趣小组”所写的两个结论的正确性.
类比探究:
(1)解决完“兴趣小组”的两个问题后,老师让同学们继续探究,再提出新的问题;“智慧小组“提出的问题是:如图(1),将正方形OEFG在图(1)的基础上旋转一定的角度,当OE与CB的延长线交于点M,OG与DC的延长线交于点N,则“兴趣小组”所写的两个结论是否仍然成立?请说明理由.
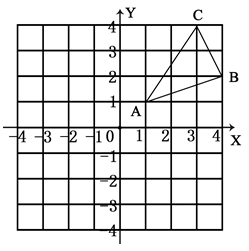
20.(8分)如图,△ABC三个顶点的坐标分别为A(1,1),B(4,2),C(3,4).
(1) 请画出△ABC向左平移5个单位长度后得到的△A![]() B
B![]() C
C![]() ;
;
(2) 请画出△ABC关于原点对称的△A![]() B
B![]() C
C![]() ;
;
(3) 在![]() 轴上求作一点P,使△PAB的周长最小,请画出△PAB,并直接写出P的坐标.
轴上求作一点P,使△PAB的周长最小,请画出△PAB,并直接写出P的坐标.
21.(10分)计算:(![]() +
+![]() )×
)×![]()
22.(10分)已知四边形ABCD是菱形,AB=4,∠ABC=60°,∠EAF的两边分别与射线CB,DC相交于点E,F,且∠EAF=60°.
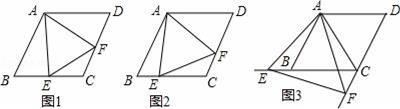
(1)如图1,当点E是线段CB的中点时,直接写出线段AE,EF,AF之间的数量关系;
(2)如图2,当点E是线段CB上任意一点时(点E不与B、C重合),求证:BE=CF;
(3)如图3,当点E在线段CB的延长线上,且∠EAB=15°时,求点F到BC的距离.
23.(12分)某中学积极开展跳绳锻炼,一次体育測试后,体育委员统计了全班同学单位时间的跳绳次数,列出了频数分布表和頻数分布直方图,如图:
次数 | 频数 |
|
|
| 4 |
| 18 |
| 13 |
| 8 |
|
|
| 1 |
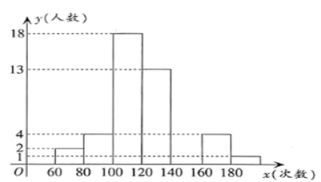
(1)补全频数分布表和频数分布直方图;
(2)表中组距是 次,组数是 组;
(3)跳绳次数在![]() 范围的学生有 人,全班共有 人;
范围的学生有 人,全班共有 人;
(4)若规定跳绳次数不低于140次为优秀,求全班同学跳绳的优秀率是多少?
参考答案
一、选择题:本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1、B
2、C
3、A
4、A
5、B
6、B
7、D
8、C
9、C
10、B
11、A
12、B
二、填空题(每题4分,满分20分,将答案填在答题纸上)
13、![]() 或
或![]()
14、1
15、1.
16、![]()
17、![]()
三、解答题 (本大题共7小题,共64分.解答应写出文字说明、证明过程或演算步骤.)
18、(1)证明见解析,(2)当AB=AC时,四边形ADCF为矩形,理由见解析.
19、(1)详见解析;(1)结论①不成立,结论②成立,理由详见解析.
20、(1)图形见解析;
(2)图形见解析;
(3)图形见解析,点P的坐标为:(2,0)
21、6+2![]() .
.
22、(1)AE=EF=AF;(2)证明过程见解析;(3)3-![]()
23、(1)见解析,(2)表中组距是20次,组数是7组;(3)31人,50人;(4)26%
四川省都江堰市初2023-2024学年数学九上期末学业质量监测模拟试题含答案: 这是一份四川省都江堰市初2023-2024学年数学九上期末学业质量监测模拟试题含答案,共8页。试卷主要包含了如果双曲线y=经过点,下列事件中,为必然事件的是等内容,欢迎下载使用。
湖北省2022-2023学年数学七年级第二学期期末质量跟踪监视模拟试题含答案: 这是一份湖北省2022-2023学年数学七年级第二学期期末质量跟踪监视模拟试题含答案,共6页。试卷主要包含了考生要认真填写考场号和座位序号,下列计算中正确的是等内容,欢迎下载使用。
江西省2022-2023学年数学七年级第二学期期末质量跟踪监视模拟试题含答案: 这是一份江西省2022-2023学年数学七年级第二学期期末质量跟踪监视模拟试题含答案,共6页。试卷主要包含了考生必须保证答题卡的整洁等内容,欢迎下载使用。












