


吉林省吉林市第12中学2022-2023学年七年级数学第二学期期末经典试题含答案
展开吉林省吉林市第12中学2022-2023学年七年级数学第二学期期末经典试题
(时间:120分钟 分数:120分)
学校_______ 年级_______ 姓名_______
注意事项
1.考试结束后,请将本试卷和答题卡一并交回.
2.答题前,请务必将自己的姓名、准考证号用0.5毫米黑色墨水的签字笔填写在试卷及答题卡的规定位置.
3.请认真核对监考员在答题卡上所粘贴的条形码上的姓名、准考证号与本人是否相符.
4.作答选择题,必须用2B铅笔将答题卡上对应选项的方框涂满、涂黑;如需改动,请用橡皮擦干净后,再选涂其他答案.作答非选择题,必须用05毫米黑色墨水的签字笔在答题卡上的指定位置作答,在其他位置作答一律无效.
5.如需作图,须用2B铅笔绘、写清楚,线条、符号等须加黑、加粗.
一、选择题(每小题3分,共30分)
1.如图,从几何图形的角度看,下列这些图案既是中心对称图形又是轴对称图形的是( )
A.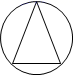 B.
B. C.
C. D.
D.
2.如图1,四边形![]() 中,
中,![]() ,
,![]() .动点
.动点![]() 从点
从点![]() 出发沿折线
出发沿折线![]() 方向以
方向以![]() 单位/秒的速度匀速运动,在整个运动过程中,
单位/秒的速度匀速运动,在整个运动过程中,![]() 的面积
的面积![]() 与运动时间
与运动时间![]() (秒)的函数图像如图2所示,则AD等于( )
(秒)的函数图像如图2所示,则AD等于( )
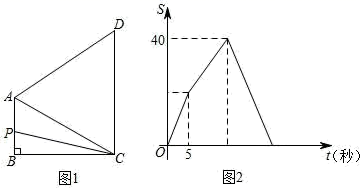
A.10 B.![]() C.8 D.
C.8 D.![]()
3.下列计算正确的是( )
A.![]() B.
B.![]() C.
C.![]() D.﹣
D.﹣![]()
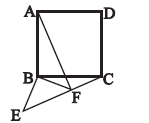
4.如图,以正方形![]() 的顶点
的顶点![]() 为直角顶点,作等腰直角三角形
为直角顶点,作等腰直角三角形![]() ,连接
,连接![]() 、
、![]() ,当
,当![]() 、
、![]() 、
、![]() 三点在--条直线上时,若
三点在--条直线上时,若![]() ,
,![]() ,则正方形
,则正方形![]() 的面积是( )
的面积是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
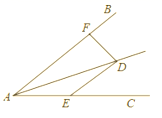
5.如图:![]() ,
,![]() ,
,![]() ,若
,若![]() ,则
,则![]() 等于( )
等于( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
6.下列图形中的曲线不表示y是x的函数的是( )
A.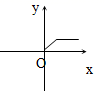 B.
B.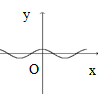 C.
C.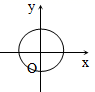 D.
D.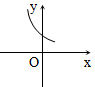
7.某特快列车在最近一次的铁路大提速后,时速提高了30千米![]() 小时,则该列车行驶350千米所用的时间比原来少用1小时,若该列车提速前的速度是x千米
小时,则该列车行驶350千米所用的时间比原来少用1小时,若该列车提速前的速度是x千米![]() 小时,下列所列方程正确的是
小时,下列所列方程正确的是![]()
A.![]() B.
B.![]()
C.![]() D.
D.![]()
8.下列函数中,是正比例函数的是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
9.关于![]() 的一元二次方程
的一元二次方程![]() 有实数根,则
有实数根,则![]() 的最大整数值是( )
的最大整数值是( )
A.1 B.0 C.-1 D.不能确定
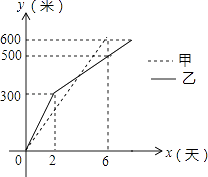
10.我市某小区实施供暖改造工程,现甲、乙两工程队分别同时开挖两条600米长的管道,所挖管道长度y(米)与挖掘时间x(天)之间的关系如图所示,则下列说法中,正确的个数有( )个.
①甲队每天挖100米;
②乙队开挖两天后,每天挖50米;
③当x=4时,甲、乙两队所挖管道长度相同;
④甲队比乙队提前2天完成任务.
A.1 ![]() B.2
B.2 ![]() C.3
C.3 ![]() D.4
D.4
二、填空题(本大题共有6小题,每小题3分,共18分)
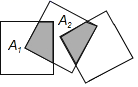
11.如图,三个边长均为1的正方形按如图所示的方式摆放,A1,A2分别是正方形对角线的交点,则重叠部分的面积和为______.
12.已知线段a,b,c能组成直角三角形,若a=3,b=4,则c=_____.
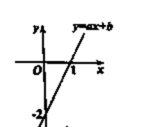
13.一次函数![]() 的图象如图所示,不等式
的图象如图所示,不等式![]() 的解集为__________.
的解集为__________.
14.已知分式方程![]() +
+![]() =
=![]() ,设
,设![]() ,那么原方程可以变形为__________
,那么原方程可以变形为__________
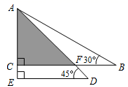
15.将一副三角尺如图所示叠放在一起,若AB=8cm,则阴影部分的面积是_____cm1.
16.某市出租车的收费标准如下:起步价5元,即![]() 千米以内(含
千米以内(含![]() 千米)收费
千米)收费![]() 元,超过
元,超过![]() 千米的部分,每千米收费
千米的部分,每千米收费![]() 元.(不足
元.(不足![]() 千米按
千米按![]() 千米计算)求车费
千米计算)求车费![]() (元)与行程
(元)与行程![]() (千米)的关系式________.
(千米)的关系式________.
三、解下列各题(本大题共8小题,共72分)
17.(8分)如图,在菱形![]() 中,
中,![]() 是
是![]() 的中点,且
的中点,且![]() ,
,![]() ;
;
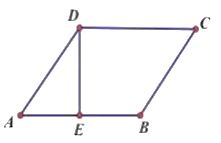
求:(1)![]() 的大小;
的大小;
(2)菱形![]() 的面积.
的面积.
18.(8分)某厂为了检验甲、乙两车间生产的同一种零件的直径的合格情况,随机各抽取了10个样品进行检测,已知零件的直径均为整数,整理数据如下:(单位:![]() )
)
| 170~174 | 175~179 | 180~184 | 185~189 |
甲车间 | 1 | 3 | 4 | 2 |
乙车间 | 0 | 6 | 2 | 2 |
(1)分别计算甲、乙两车间生产的零件直径的平均数;
(2)直接说出甲、乙两车间生产的零件直径的中位数都在哪个小组内,众数是否在其相应的小组内?
(3)若该零件的直径在![]() 的范围内为合格,甲、乙两车间哪一个车间生产的零件直径合格率高?
的范围内为合格,甲、乙两车间哪一个车间生产的零件直径合格率高?
19.(8分)(1)已知点A(2,0)在函数y=kx+3的图象上,求该函数的表达式并画出图形;
(2)求该函数图象与坐标轴围成的三角形的面积.
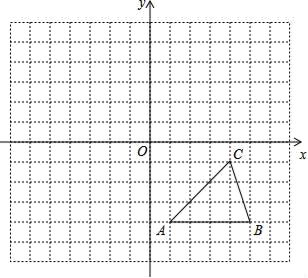
20.(8分)如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,点C的坐标为(4,﹣1).
①把△ABC向上平移5个单位后得到对应的△A1B1C1,画出△A1B1C1;
②以原点O为对称中心,再画出与△ABC关于原点对称的△A2B2C2,并写出点C2的坐标.
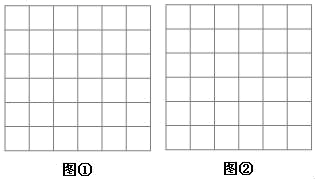
21.(8分)如图,正方形网格中,每个小正方形的边长均为1,每个小正方形的顶点叫格点.
(1)在图①中,以格点为端点,画线段MN=![]() ;
;
(2)在图②中,以格点为顶点,画正方形ABCD,使它的面积为1.
22.(10分)何老师安排喜欢探究问题的小明解决某个问题前,先让小明看了一个有解答过程的例题.
例:若m2+2mn+2n2﹣6n+9=0,求m和n的值.
解:∵m2+2mn+2n2﹣6n+9=0
∴m2+2mn+n2+n2﹣6n+9=0
∴(m+n)2+(n﹣3)2=0
∴m+n=0,n﹣3=0∴m=﹣3,n=3
为什么要对2n2进行了拆项呢?
聪明的小明理解了例题解决问题的方法,很快解决了下面两个问题.相信你也能很好的解决下面的这两个问题,请写出你的解题过程..
解决问题:
(1)若x2﹣4xy+5y2+2y+1=0,求xy的值;
(2)已知a、b、c是△ABC的三边长,满足a2+b2=10a+12b﹣61,c是△ABC中最短边的边长,且c为整数,那么c可能是哪几个数?
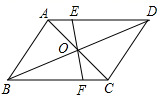
23.(10分)已知:如图,在□ABCD中,对角线AC,BD相交于点O,直线EF过点O,交DA于点E,交BC于点F.求证:OE=OF,AE=CF,DE=BF
24.(12分)潮州市某学校为了改善办学条件,购置一批电子白板和台式电脑合共24台.经招投标,一台电子白板每台9000元,一台台式电脑每台3000元,设学校购买电子白板和台式电脑总费用为![]() 元,购买了
元,购买了![]() 台电子白板,并且台式电脑的台数不超过电子白板台数的3倍.
台电子白板,并且台式电脑的台数不超过电子白板台数的3倍.
(1)请求出![]() 与
与![]() 的函数解析式,并直接写出
的函数解析式,并直接写出![]() 的取值范围
的取值范围
(2)请问当购买多少台电子白板时,学校购置电子白板和台式电脑的总费用最少,最少多少钱?
参考答案
一、选择题(每小题3分,共30分)
1、B
2、B
3、C
4、C
5、C
6、C
7、B
8、B
9、C
10、D
二、填空题(本大题共有6小题,每小题3分,共18分)
11、![]()
12、5或![]()
13、![]()
14、![]() =
=![]()
15、2
16、![]()
三、解下列各题(本大题共8小题,共72分)
17、(1)![]() ;(2)
;(2)![]() .
.
18、(1)![]() ,
, ![]() ;(2)甲中位数在180-184组,乙中位数在175-179组,众数不一定在相应的小组内;(3)乙车间的合格率高
;(2)甲中位数在180-184组,乙中位数在175-179组,众数不一定在相应的小组内;(3)乙车间的合格率高
19、(1)![]() ,画图形见解析;(2)
,画图形见解析;(2)![]()
20、①见解析;②见解析,点C2坐标为(﹣4,1).
21、(1)画图见解析;(2)画图见解析.
22、(1)![]() 1;(2)c为2,3,1.
1;(2)c为2,3,1.
23、证明见解析
24、 (1)![]() (
(![]() ,且
,且![]() 为整数);(2)当购买电子白板6台,台式电脑18台学校总费用最少钱,最少是108000元.
为整数);(2)当购买电子白板6台,台式电脑18台学校总费用最少钱,最少是108000元.
2023-2024学年吉林省吉林市第七中学九上数学期末经典模拟试题含答案: 这是一份2023-2024学年吉林省吉林市第七中学九上数学期末经典模拟试题含答案,共9页。试卷主要包含了分式方程的根是,如图所示的几何体的左视图为等内容,欢迎下载使用。
2023-2024学年吉林省吉林市第12中学数学九上期末联考试题含答案: 这是一份2023-2024学年吉林省吉林市第12中学数学九上期末联考试题含答案,共7页。
吉林省长春市第108中学2022-2023学年数学七年级第二学期期末经典模拟试题含答案: 这是一份吉林省长春市第108中学2022-2023学年数学七年级第二学期期末经典模拟试题含答案,共7页。试卷主要包含了已知二次函数,打开某洗衣机开关,在洗涤衣服时,下列说法正确的是,一次函数,当时,x的取值范围是等内容,欢迎下载使用。












