沪教版数学八年级上册 第十九章几何证明单元测试

第十九章 几何证明 单元测试

一、选择题
1.命题：①对顶角相等；②垂直于同一条直线的两直线平行；③相等的角是对   顶角；④同位角相等．其中假命题有（　　）

A．1个    B．2个    C．3个    D．4个

2．如图，AC=AD，BC=BD，则有（　　）

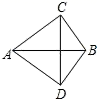
 A. AB垂直平分CD            B. CD垂直平分AB

 C. AB与CD互相垂直平分        D. CD平分∠ACB

3．如果直角三角形的三条边为2，4，a，那么a的取值可以有（    ）
　　A.0个　 　B.1个　 　C.2个　　 D.3个 　　　　　　　　　　　　　　　　

4．按下列各组数据能组成直角三角形的是（   ）
　　A.11，15，13 　　B.1，4，5　　 C.8，15，17 　　D.4，5，6

5．已知直角三角形一个锐角60°，斜边长为1，那么此直角三角形的周长是（    ）
　　A． 　　　B．3 　　　C． 　　　D．

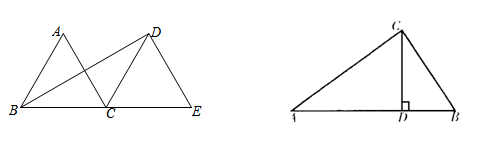6．如图，△ABC和△DCE都是边长为4的等边三角形，点B、C、E在同一条直线上，连接 BD，则BD的长为（    ）
A． 　　　B．　　　 C． 　　　D．
　　       

第6题                                    第7题

7．如图所示，△ABC中，CD⊥AB于D，若AD=2BD，AC=5，BC=4，则BD的长为（    ）
　A．　　 　 B． 　 　　C．1 　　 　D．

8．直角三角形有一条直角边长为13，另外两条边长都是自然数，则周长为（    ）
　　A．182 　　　B．183 　　　C．184 　　　D．185

二、填空题

9.到定点A的距离为4cm的点的轨迹是                                        .           

10．把命题“等角的补角相等”改写成“如果……那么……”的形式是结果_________，那么__________．

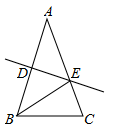
11．如图，在△ABC中，∠B=30°，ED垂直平分BC，ED=3．则CE长为　  　．

12．如图，在△ABC中，边AB的垂直平分线交边AC于E点，△ABC与△EBC的周长分别是24和14，则AB=　    　．

13. 如图，已知正方形的边长为3，为边上一点，．以点为中心，把△顺时针旋转，得△，连接，则的长等于___________．　

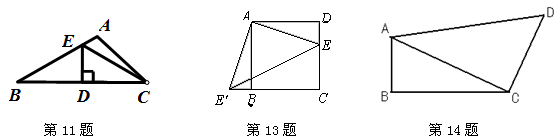
14. 如图，在四边形ABCD中，AB=1，BC=2，CD=2，AD=3，且∠ABC=90°，连结AC，则△ACD的面积

为       .

15．一个正方体物体沿斜坡向下滑动，其截面如图所示.正方形DEFH的边长为2米，坡角∠A＝30°，∠B＝90°，BC＝6米. 当正方形DEFH运动到什么位置，即当AE等于      米时，有DC＝AE＋BC.

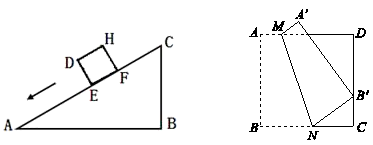
第15题                           第16题

16．如图，四边形ABCD是边长为9的正方形纸片，为CD边上的点，=3．将纸片沿某条直线折叠，使点B落在点处，点A的对应点为，折痕分别与AD，BC边交于点M，N．则BN的长为         .

三、解答题

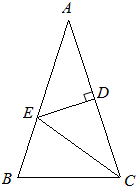
17. 如图，△ABC中，AB=AC，∠A=36°，AC的垂直平分线交AB于E，D为垂足，连接EC．

（1）求∠ECD的度数；

（2）若CE=5，求BC长．

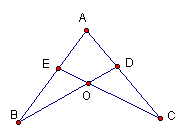
18.如图，已知AB=AC,AD=AE,DB与CE相交于O
　　(1) 若DB⊥AC,CE⊥AB,D,E为垂足，试判断点O的位置及OE与OD的大小关系，并证明你的结论。
　　(2) 若D，E不是垂足，是否有同样的结论？并证明你的结论。
　　　　　　　　　　　　　　　　                            
19．阅读下列一段文字，然后回答下列问题：

已知平面内两点M（x1，y1）、N（x2，y2），则这两点间的距离可用下列公式计算：MN=．

例如：已知P（3，1）、Q（1，﹣2），则这两点的距离PQ==．

特别地，如果两点M（x1，y1）、N（x2，y2）所在的直线与坐标轴重合或平行于坐标轴或垂直于坐标轴，那么这两点间的距离公式可简化为MN=|x1﹣x2|或|y1﹣y2|．

（1）已知A（1，2）、B（﹣2，﹣3），试求A、B两点间的距离；

（2）已知A、B在平行于y轴的同一条直线上，点A的纵坐标为5，点B的纵坐标为﹣1，试求A、B两点间的距离；

（3）已知△ABC的顶点坐标分别为A（0，4）、B（﹣1，2）、C（4，2），你能判定△ABC的形状吗？请说明理由．

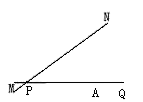
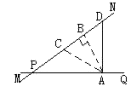
20. 如图，公路MN和公路PQ在点P处交汇，且∠QPN＝30°，点A处有一所中学，AP＝160m。假设拖拉机行驶时，周围100m以内会受到噪音的影响，那么拖拉机在公路MN上沿PN方向行驶时，学校是否会受到噪声影响？请说明理由，如果受影响，已知拖拉机的速度为18km/h，那么学校受影响的时间为多

少秒？
　　　　　　　　　　　　　　　　　　                          　

参考答案

一、选择题

1．C

2．A

3．C

4. C

5．D

6．D

7．B

8．A

二、填空题

9．以顶点A为圆心、4cm的长为半径的圆.

10．如果两个角是另两个相等角的补角，那么这两个角相等.

11．6

12.10

13.

14.

15.

16.5
 

三、解答题

17.解：（1）∵DE垂直平分AC，

∴CE=AE，∴∠ECD=∠A=36°；

（2）∵AB=AC，∠A=36°，

∴∠B=∠ACB=72°，

∴∠BEC=∠A+∠ECD=72°，

∴∠BEC=∠B，

∴BC=EC=5．

答：（1）∠ECD的度数是36°；（2）BC长是5．

18．解：（1）∵AB=AC,AD=AE
　　　　 ∴BE=CD
　　　　 ∵DB⊥AC,CE⊥AB,
　　　　 ∴∠BEO=∠CDO=90°
　　　　 在△BEO和△CDO中
　　　　
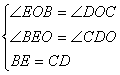
　　　　 ∴△BEO≌△CDO
　　　　 ∴EO=DO
　　　　 ∵EO⊥AB,DO⊥AC
　　　　 ∴点O在∠A的平分线上
　　（2）点D,E不是垂足时，（1）的结论仍然成立，连接AO
　　　　 在△ABD和△ACE中
　　　　
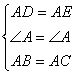
　　　　 ∴△ABD≌△ACE
　　　　 ∴∠B=∠C
　　　　 ∵AB=AC,AD=AE
　　　　 ∴EB=CD
　　　　 在△BEO和△CDO中
　　　　
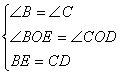
　　　　 ∴△BEO≌△CDO
　　　　 ∴EO=DO
　　　　 连接AO，则：
　　　　 在△AEO和△ADO中
　　　　
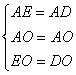
　　　　 ∴△AEO≌△ADO
　　　　 ∴∠EAO=∠DAO
　　　　 ∴O点在∠A的角平分线上
 

19.解：（1）AB==；

（2）AB=5﹣（﹣1）=6；

（3）△ABC为直角三角形．理由如下：

∵AB==，AC==2，BC==5，

∴AB2+AC2=BC2，

∴△ABC为直角三角形．

20.解：

        作AB⊥MN，垂足为B.
　　　　在 RtΔABP中，∵∠ABP＝90°，∠APB＝30°， AP＝160，
　　　　　∴ AB＝AP＝80. （直角三角形中，30°所对的直角边等于斜边的一半）
　　　　　∵点 A到直线MN的距离小于100m，
　　　　　∴这所中学会受到噪声的影响.
　　　　　如图，假设拖拉机在公路 MN上沿PN方向行驶到点C处时学校开始受到影响，

那么AC＝100(m)，
　　　　　由勾股定理得： BC2＝1002－802＝3600， ∴ BC＝60m.
　　　　　　　　　　　　　　　　
　　　　　同理，假设拖拉机行驶到点D处时学校开始不受影响，那么AD＝100(m)，BD＝60(m)，
　　　　　∴ CD＝120(m).
　　　　　∵拖拉机行驶的速度为 : 18km/h＝5m/s
　　　　　∴t＝120m÷5m/s＝24s.
　　     答：拖拉机在公路 MN上沿PN方向行驶时，学校会受到噪声影响，学校受影响的时间为24秒.