北京市石景山区2022-2023学年数学七下期末达标测试试题含答案

这是一份北京市石景山区2022-2023学年数学七下期末达标测试试题含答案，共7页。试卷主要包含了考生必须保证答题卡的整洁，函数y＝中自变量x的取值范围是，若分式有意义，则的取值范围是，下列计算或化简正确的是等内容，欢迎下载使用。
北京市石景山区2022-2023学年数学七下期末达标测试试题（时间：120分钟             分数：120分） 学校_______            年级_______        姓名_______ 注意事项：1．答卷前，考生务必将自己的姓名、准考证号、考场号和座位号填写在试题卷和答题卡上。用2B铅笔将试卷类型（B）填涂在答题卡相应位置上。将条形码粘贴在答题卡右上角"条形码粘贴处"。2．作答选择题时，选出每小题答案后，用2B铅笔把答题卡上对应题目选项的答案信息点涂黑；如需改动，用橡皮擦干净后，再选涂其他答案。答案不能答在试题卷上。3．非选择题必须用黑色字迹的钢笔或签字笔作答，答案必须写在答题卡各题目指定区域内相应位置上；如需改动，先划掉原来的答案，然后再写上新答案；不准使用铅笔和涂改液。不按以上要求作答无效。4．考生必须保证答题卡的整洁。考试结束后，请将本试卷和答题卡一并交回。 一、选择题(每小题3分,共30分)1．某工厂现在平均每天比原计划多生产50台机器，现在生产600台机器所用的时间与原计划生产450台机器所用的时间相同．若设原计划平均每天生产x台机器，则可列方程为(   )A．＝ B．＝ C．＝ D．＝2．下列四组线段中，能组成直角三角形的是　　A．，， B．，，C．，， D．，，3．若一个多边形的内角和是外角和的5倍，则这个多边形的边数是（　　）A．12 B．10 C．8 D．114．到三角形三个顶点的距离相等的点是三角形（ ）的交点．A．三个内角平分线 B．三边垂直平分线C．三条中线 D．三条高5．龙华地铁4号线北延计划如期开工，由清湖站开始，到达观澜的牛湖站，长约10.770公里，其中需修建的高架线长1700m．在修建完400m后，为了更快更好服务市民，采用新技术，工效比原来提升了25%．结果比原计划提前4天完成高架线的修建任务．设原计划每天修建xm，依题意列方程得（　　）A． B．C． D．6．函数y＝中自变量x的取值范围是（  ）A．x＞2 B．x≥2 C．x≤2 D．x≠27．若不等式组的解集为，则图中表示正确的是（      ）A． B． C． D．8．若分式有意义，则的取值范围是（    ）A．     B． C． D．9．下列计算或化简正确的是（　　）A． B．C． D．10．反比例函数图象上有，两点，则与的大小关系是（    ）A． B． C． D．不确定二、填空题(本大题共有6小题，每小题3分，共18分)11． “I am a good student．”这句话的所有字母中，字母“a”出现的频率是______12．如图，正方形ABCD中，AB=6，点E在边CD上，且CD=3DE，将△ADE沿AE对折至△AEF，延长EF交边BC于点G，连接AG，CF，则下列结论：①△ABG≌△AFG；②BG=CG；③AG∥CF；④S△EGC=S△AFE；⑤S△FGC=，其中正确的结论有__________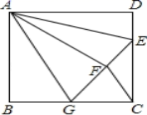．13．矩形的对角线与相交于点，，，分别是，的中点，则的长度为________.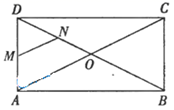14．在一次射击比赛中，甲、乙两名运动员 10 次射击的平均成绩都是 7 环，其中甲的成绩的方差为 1.2，乙的成绩的方差为 3.9，由此可知_____的成绩更稳定．15．函数中自变量x的取值范围是_______.16．在关系式V=31-2t中，V随着t的变化而变化，其中自变量是_____，因变量是_____，当t=_____时，V=1．三、解下列各题(本大题共8小题，共72分)17．（8分）如图，已知平面直角坐标系中，直线与x轴交于点A，与y轴交于B，与直线y＝x交于点C．（1）求A、B、C三点的坐标；（2）求△AOC的面积；（3）已知点P是x轴正半轴上的一点，若△COP是等腰三角形，直接写点P的坐标．   18．（8分）如图1，在△ABC中，∠BAC=90°，AB=AC，在△ABC内部作△CED，使∠CED=90°，E在BC上，D在AC上，分别以AB，AD为邻边作平行四边形ABFD，连接AF、AE、EF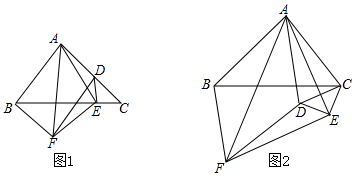．（1）证明：AE=EF；（2）判断线段AF，AE的数量关系，并证明你的结论；（3）在图（1）的基础上，将△CED绕点C逆时针旋转，请判断（2）问中的结论是否成立？若成立，结合图（2）写出证明过程；若不成立，请说明理由   19．（8分）如图，一次函数y＝kx+b（k≠0）经过点B（0，1），且与反比例函数y＝（m≠0）的图象在第一象限有公共点A（1，2）．（1）求一次函数与反比例函数的解析式；（2）根据图象写出当x取何值时，一次函数的值小于反比例函数的值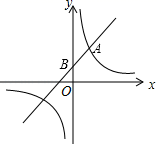？   20．（8分）一个二次函数的图象经过三点.求这个二次函数的解析式并写出图象的开口方向、对称轴和顶点.   21．（8分）在研究反比例函数y＝﹣的图象时，我们发现有如下性质：(1)y＝﹣的图象是中心对称图形，对称中心是原点．(2)y＝﹣的图象是轴对称图形，对称轴是直线y＝x，y＝﹣x．(3)在x＜0与x＞0两个范围内，y随x增大而增大；类似地，我们研究形如：y＝﹣+3的函数：(1)函数y＝﹣+3图象是由反比例函数y＝﹣图象向____平移______个单位，再向_______平移______个单位得到的．(2)y＝﹣+3的图象是中心对称图形，对称中心是______．(3)该函数图象是轴对称图形吗？如果是，请求出它的对称轴，如果不是，请说明理由．(4)对于函数y＝，x在哪些范围内，y随x的增大而增大？   22．（10分）某区对即将参加中考的初中毕业生进行了一次视力抽样调查，绘制出频数分布表和频数分布直方图的一部分．请根据图表信息回答下列问题：视力频数（人）频率4.0≤x＜4.3200.14.3≤x＜4.6400.24.6≤x＜4.9700.354.9≤x＜5.2a0.35.2≤x＜5.510b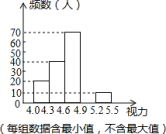（1）本次调查的样本为        ，样本容量为         ；（2）在频数分布表中，组距为           ，a=         ，b=        ，并将频数分布直方图补充完整；（3）若视力在4.6以上（含4.6）均属正常，计算抽样中视力正常的百分比．   23．（10分）中国古代有着辉煌的数学成就，《周牌算经》、《九章算术》、《海岛算经》、《孙子算经》等是我国古代数学的重要文献.（1）小聪想从这4部数学名著中随机选择1部阅读，求他选中《九章算术》的概率；（2）小聪拟从这4部数学名著中选择2部作为假课外拓展学习内容，用列表或树状图求选中的名著恰好是《九章算术》和《周牌算经》的概率.   24．（12分）在某市举办的“读好书，讲礼仪”活动中，东华学校积极行动，各班图书角的新书、好书不断增多，除学校购买外，还有师生捐献的图书．下面是七年级（1）班全体同学捐献图书的情况统计图：请你根据以上统计图中的信息，解答下列问题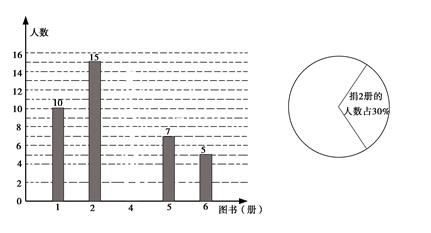：（1）该班有学生多少人？（2）补全条形统计图；（3）七（1）班全体同学所捐献图书的中位数和众数分别是多少？   参考答案 一、选择题(每小题3分,共30分)1、C2、D3、A4、B5、C6、C7、C8、B9、D10、B 二、填空题(本大题共有6小题，每小题3分，共18分)11、12、①②③④⑤13、114、甲15、x≥-316、t    V    15     三、解下列各题(本大题共8小题，共72分)17、（1）A（－4，0）；B（0，2）；C（4，4）；（2）1；（3）（4，0）或（1，0）或（，0）．18、（1）证明见解析；（2）AF=AE．证明见解析；（3）AF=AE成立．证明见解析.19、（1）y＝x+1；y＝；（2）当x＜﹣2或0＜x＜1时，一次函数的值小于反比例函数的值．20、,图象开口向上，对称轴直线，顶点.21、（1）右，2，上，1；（2）(2，1)；（1）是轴对称图形，对称轴是：y＝x+1和y＝﹣x+2；（4）x＜2或x＞2.22、（1）从中抽取的200名即将参加中考的初中毕业生的视力；200；（2）0.3；60；0.05，见解析；（3）70%．23、（1）；（2）.24、（1）因为捐2本的人数是15人，占30％，所以该班人数为＝50（2）根据题意知，捐4本的人数为：50－(10＋15＋7＋5)＝1．(如图)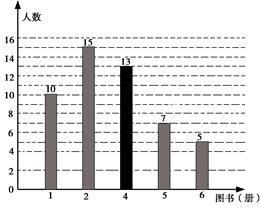（3）七（1）班全体同学所捐献图书的中位数是＝3(本)，众数是2本．