


北京市怀柔区九级2022-2023学年数学七下期末达标检测模拟试题含答案
展开北京市怀柔区九级2022-2023学年数学七下期末达标检测模拟试题
(时间:120分钟 分数:120分)
学校_______ 年级_______ 姓名_______
考生须知:
1.全卷分选择题和非选择题两部分,全部在答题纸上作答。选择题必须用2B铅笔填涂;非选择题的答案必须用黑色字迹的钢笔或答字笔写在“答题纸”相应位置上。
2.请用黑色字迹的钢笔或答字笔在“答题纸”上先填写姓名和准考证号。
3.保持卡面清洁,不要折叠,不要弄破、弄皱,在草稿纸、试题卷上答题无效。
一、选择题:本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.甲、乙、丙、丁四人进行射击测试,每人10次射击的平均成绩恰好都是9.4环,
方差分别是![]() ,
,![]() ,
,![]() ,
,![]() .在本次射击测试中,成绩最
.在本次射击测试中,成绩最
稳定的是( )
A.甲 B.乙 C.丙 D.丁
2.下列图形中的曲线不表示y是x的函数的是( )
A.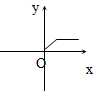 B.
B.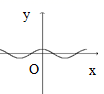 C.
C.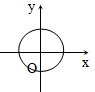 D.
D.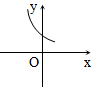
3.如图,△ABC以点C为旋转中心,旋转后得到△EDC,已知AB=1.5,BC=4,AC=5,则DE=( )
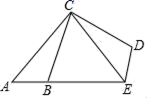
A.1.5 B.3 C.4 D.5
4.如图,已知直线y1=x+a与y2=kx+b相交于点P(﹣1,2),则关于x的不等式x+a>kx+b的解集正确的是( )
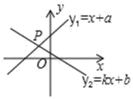
A.x>﹣1 B.x>1 C.x<1 D.x<﹣1
5.下列二次根式能与![]() 合并的是( )
合并的是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
6.如图,已知一次函数![]() ,
,![]() 随着
随着![]() 的增大而增大,且
的增大而增大,且![]() ,则在直角坐标系中它的图象大致是( )
,则在直角坐标系中它的图象大致是( )
A.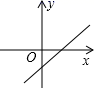 B.
B.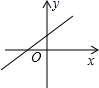 C.
C.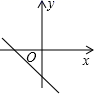 D.
D.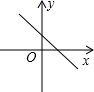
7.在数轴上用点B表示实数b.若关于x的一元二次方程x2+bx+1=0有两个相等的实数根,则( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
8.如图,菱形ABCD的一边中点M到对角线交点O的距离为5cm,则菱形ABCD的周长为( )
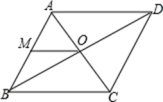
A.5cm B.10cm C.20cm D.40cm
9.在下列交通标志中,是中心对称图形的是( )
A. B.
B.
C. D.
D.
10.下列说法正确的是( )
A.对应边都成比例的多边形相似 B.对应角都相等的多边形相似
C.边数相同的正多边形相似 D.矩形都相似
11.如图,两个直角三角形重叠在一起,将其中一个三角形沿着点B到点C的方向平移到△DEF的位置,∠B=90°,AB=8,DH=3,平移距离为4,求阴影部分的面积为( )
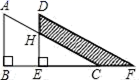
A.20 B.24 C.25 D.26
12.若线段2a+1,a,a+3能构成一个三角形,则a的范围是( )
A.a>0 B.a>1 C.a>2 D.1<a<3
二、填空题(每题4分,满分20分,将答案填在答题纸上)
13.张老师公布班上6名同学的数学竞赛成绩时,有意公布了5个人的得分:78,92,61,85,75,又公布了6个人的平均分:80,还有一个未公布,这个未公布的得分是_____.
14.已知:线段AB,BC.
求作:平行四边形ABCD.
以下是甲、乙两同学的作业.
甲:
①以点C为圆心,AB长为半径作弧;
②以点A为圆心,BC长为半径作弧;
③两弧在BC上方交于点D,连接AD,CD.
四边形ABCD即为所求平行四边形.(如图1)
乙:
①连接AC,作线段AC的垂直平分线,交AC于点M;
②连接BM并延长,在延长线上取一点D,使MD=MB,连接AD,CD.
四边形ABCD即为所求平行四边形.(如图2)
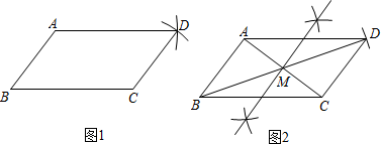
老师说甲、乙同学的作图都正确,你更喜欢______的作法,他的作图依据是:______.
15.不等式组![]() 的解集为_________.
的解集为_________.
16.已知点![]() 与点
与点![]() 关于y轴对称,则
关于y轴对称,则![]() __________.
__________.
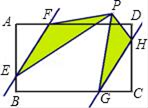
17.如图,在矩形ABCD中,AD=6,AB=4,点E、G、H、F分别在AB、BC、CD、AD上,且AF=CG=2,BE=DH=1,点P是直线EF、GH之间任意一点,连接PE、PF、PG、PH,则△PEF和△PGH的面积和等于________.
三、解答题 (本大题共7小题,共64分.解答应写出文字说明、证明过程或演算步骤.)
18.(5分)如图所示,在梯形ABCD中,AD∥BC,∠B=90°,AD=24cm,BC=26cm,动点P从点A出发沿AD方向向点D以1cm/s的速度运动,动点Q从点C开始沿着CB方向向点B以3cm/s的速度运动.点P、Q分别从点A和点C同时出发,当其中一点到达端点时,另一点随之停止运动.
(1)经过多长时间,四边形PQCD是平行四边形?
(2)经过多长时间,四边形PQBA是矩形?
(3)经过多长时间,当PQ不平行于CD时,有PQ=CD.

19.(5分)某校餐厅计划购买12张餐桌和一批餐椅,现从甲、乙两商场了解到:同一型号的餐桌报价每张均为200元,餐椅报价每把均为50元.甲商场称:每购买一张餐桌赠送一把餐椅;乙商场规定:所有餐桌椅均按报价的八五折销售.那么,学校应如何购买更优惠?
20.(8分)今年上海市政府计划年内改造1.8万个分类垃圾箱房,把原有的分类垃圾箱房改造成可以投放“干垃圾、湿垃圾、可回收垃圾、有害垃圾”四类垃圾的新型环保垃圾箱房.环卫局原定每月改造相同数量的分类垃圾箱房,为确保在年底前顺利完成改造任务,环卫局决定每月多改造250个分类垃圾箱房,提前一个月完成任务.求环卫局每个月实际改造分类垃圾箱房的数量.
21.(10分)在学校组织的“学习强国”阅读知识竞赛中,每班参加比赛的人数相同,成绩分为![]() 四个等级,其中相应等级的得分依次记为
四个等级,其中相应等级的得分依次记为![]() 分,
分,![]() 分,
分,![]() 分和
分和![]() 分.年级组长张老师将班
分.年级组长张老师将班![]() 和
和![]() 班的成绩进行整理并绘制成如下的统计图:
班的成绩进行整理并绘制成如下的统计图:
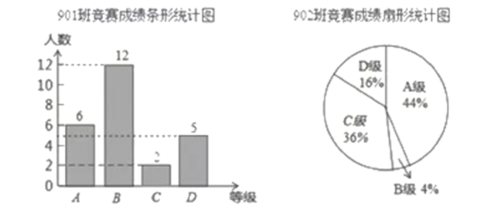
(1)在本次竞赛中,![]() 班
班![]() 级及以上的人数有多少?
级及以上的人数有多少?
(2)请你将下面的表格补充完整:
| 平均数(分) | 中位数(分) | 众数(分) |
|
|
|
|
|
|
|
|
|
|
|
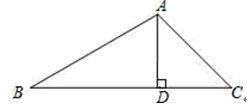
22.(10分)如图,在△ABC 中,∠B=30°,∠C=45°,AC=2![]() .求 BC 边上的高及△ABC 的面积.
.求 BC 边上的高及△ABC 的面积.
23.(12分)某市举行“传承好家风”征文比赛,已知每篇参赛征文成绩记m分(60≤m≤100),组委会从1000篇征文中随机抽取了部分参赛征文,统计了他们的成绩,并绘制了如下不完整的两幅统计图表.
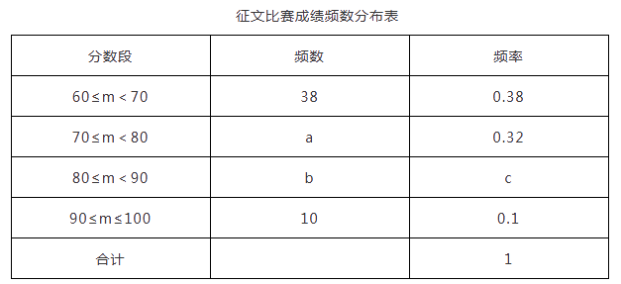
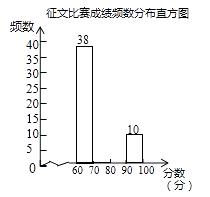
请根据以上信息,解决下列问题:
(1)征文比赛成绩频数分布表中c的值是________;
(2)补全征文比赛成绩频数分布直方图;
(3)若80分以上(含80分)的征文将被评为一等奖,试估计全市获得一等奖征文的篇数.
参考答案
一、选择题:本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1、C
2、C
3、A
4、A
5、B
6、A
7、A
8、D
9、C
10、C
11、D
12、B
二、填空题(每题4分,满分20分,将答案填在答题纸上)
13、1.
14、乙 对角线互相平分的四边形是平行四边形
15、![]()
16、-1
17、1
三、解答题 (本大题共7小题,共64分.解答应写出文字说明、证明过程或演算步骤.)
18、 (1)1s;(2) ![]() s;(3)3s.
s;(3)3s.
19、当购买的餐椅大于等于9少于32把时,到甲商场购买更优惠.
20、环卫局每个月实际改造类垃圾箱房2250个.
21、(1)21;(2)见详解
22、2,2+2![]() .
.
23、(1)0.2;(2)补全征文比赛成绩频数分布直方图见解析;(3)全市获得一等奖征文的篇数为300篇.
2023-2024学年北京市怀柔区八上数学期末达标检测模拟试题含答案: 这是一份2023-2024学年北京市怀柔区八上数学期末达标检测模拟试题含答案,共7页。试卷主要包含了考生要认真填写考场号和座位序号,下列从左到右的变形,下列各式等内容,欢迎下载使用。
林芝2022-2023学年七下数学期末达标检测模拟试题含答案: 这是一份林芝2022-2023学年七下数学期末达标检测模拟试题含答案,共5页。试卷主要包含了下列命题是假命题的是,把根号外的因式移入根号内,结果等内容,欢迎下载使用。
2022-2023学年宜宾市数学七下期末达标检测模拟试题含答案: 这是一份2022-2023学年宜宾市数学七下期末达标检测模拟试题含答案,共6页。












