2022-2023学年北京市北京市十一学校七下数学期末达标检测模拟试题含答案

2022-2023学年北京市北京市十一学校七下数学期末达标检测模拟试题

（时间：120分钟             分数：120分）

学校_______            年级_______        姓名_______

注意事项:

1．答题前，考生先将自己的姓名、准考证号码填写清楚，将条形码准确粘贴在条形码区域内。

2．答题时请按要求用笔。

3．请按照题号顺序在答题卡各题目的答题区域内作答，超出答题区域书写的答案无效；在草稿纸、试卷上答题无效。

4．作图可先使用铅笔画出，确定后必须用黑色字迹的签字笔描黑。

5．保持卡面清洁，不要折暴、不要弄破、弄皱，不准使用涂改液、修正带、刮纸刀。

一、选择题：本大题共12个小题，每小题3分，共36分.在每小题给出的四个选项中，只有一项是符合题目要求的.

1．下列运算错误的是

A． B．

C． D．

2．点关于y轴对称的点的坐标是（    ）

A． B． C． D．

3．把函数向上平移3个单位，下列在该平移后的直线上的点是(    )

A． B． C． D．

4．在平面直角坐标系中，若点P的坐标为（﹣3，2），则点P所在的象限是（　 　）

A．第一象限 B．第二象限 C．第三象限 D．第四象限

5．下列长度的三条线段能组成直角三角形的是(   )

A．，， B．，， C．，， D．，，

6．如图，在△ABC中，∠C=90°，AC=4，BC=2，点A、C分别在x轴、y轴上，当点A在x轴上运动时，点C随之在y轴上运动.在运动过程中，点B到原点的最大距离是(     )

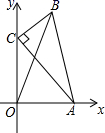
A．6 B．2 C．2 D．2＋2

7．若关于的一元二次方程有两个不相等的实数根，则的取值范围是（  ）

A． B． C．且 D．且

8．不能判断四边形ABCD是平行四边形的是(　　)

A．AB∥CD，AD∥BC B．AB=CD，AD=BC

C．AB=CD，AB∥CD D．AB=CD，AD∥BC

9．如图，DC⊥AC于C，DE⊥AB于E，并且DE＝DC，则下列结论中正确的是(　　)

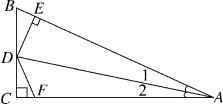
A．DE＝DF B．BD＝FD C．∠1＝∠2 D．AB＝AC

10．某学校拟建一间矩形活动室，一面靠墙(墙足够长)，中间用一道墙隔开，并在如图所示的三处各留1m宽的门，已知计划中的材料可建墙体(不包括门)总长为27m，建成后的活动室面积为75m2，求矩形活动室的长和宽，若设矩形宽为x，根据题意可列方程为(   )

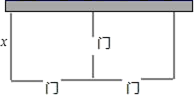
A．x(27﹣3x)＝75 B．x(3x﹣27)＝75

C．x(30﹣3x)＝75 D．x(3x﹣30)＝75

11．如图图形中，是中心对称图形，但不是轴对称图形的是（　　）

A． B．

C． D．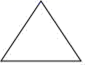

12．已知点(-2，y1)，(-1，y2)，(4，y3)在函数y=的图象上，则(   )

A．y2<y1<y3 B．y1<y2<y3 C．y3<y1<y2 D．y3<y2<y1

二、填空题（每题4分，满分20分，将答案填在答题纸上）

13．如图，边长为的正方形和边长为的正方形排放在一起，和分别是两个正方形的对称中心，则的面积为________．

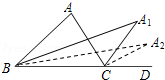
14．如图，在△ABC中，∠A=α．∠ABC与∠ACD的平分线交于点A1，得∠A1；∠A1BC与∠A1CD的平分线相交于点A2，得∠A2； …；∠A2011BC与∠A2011CD的平分线相交于点A2012，得∠A2012，则∠A2012=_____．

15．频数直方图中，一小长方形的频数与组距的比值是6，组距为3，则该小组的频数是_____．

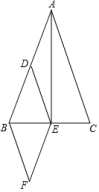
16．如图，在△ABC中，AB＝AC，E，F分别是BC，AC的中点，以AC为斜边作Rt△ADC，若∠CAD＝∠BAC＝45°，则下列结论：①CD∥EF；②EF＝DF；③DE平分∠CDF；④∠DEC＝30°；⑤AB＝CD；其中正确的是_____（填序号）

17．将一次函数y＝5x﹣1的图象向上平移3个单位，所得直线不经过第_____象限．

三、解答题 （本大题共7小题，共64分.解答应写出文字说明、证明过程或演算步骤.）

18．（5分）如图，在中，，是中线，点是的中点，连接，且，

（1）求证：四边形是菱形；

（2）若，直接写出四边形的面积．

19．（5分）如图，△ABC与△CDE都是等边三角形，点E、F分别在AC、BC上，且EF∥AB

（1）求证：四边形EFCD是菱形；

（2）设CD＝2，求D、F两点间的距离．

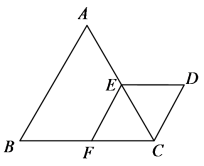
20．（8分）如图所示，矩形OABC的邻边OA、OC分别与x、y轴重合，矩形OABC的对称中心P(4，3)，点Q由O向A以每秒1个单位速度运动，点M由C向B以每秒2个单位速度运动，点N由B向C以每秒2个单位速度运动，设运动时间为t秒，三点同时出发，当一点到达终点时同时停止.

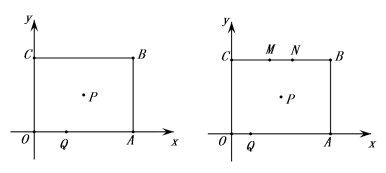
（1）根据题意，可得点B坐标为__________，AC＝_________；

（2）求点Q运动几秒时，△PCQ周长最小?

（3）在点M、N、Q的运动过程中，能否使以点O、Q、M、N为顶点的四边形是平行四边形？若能，请求出t值；若不能，请说明理由．

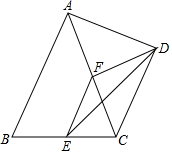
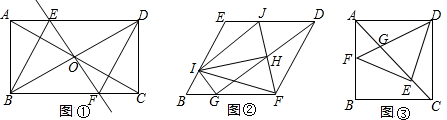
21．（10分） (1)如图①，在矩形ABCD中，对角线AC与BD相交于点O，过点O作直线EF⊥BD，交AD于点E，交BC于点F，连接BE、DF，且BE平分∠ABD．

①求证：四边形BFDE是菱形；

②直接写出∠EBF的度数；

(2)把(1)中菱形BFDE进行分离研究，如图②，点G、I分别在BF、BE边上，且BG=BI，连接GD，H为GD的中点，连接FH并延长，交ED于点J，连接IJ、IH、IF、IG.试探究线段IH与FH之间满足的关系，并说明理由；

(3)把(1)中矩形ABCD进行特殊化探究，如图③，当矩形ABCD满足AB=AD时，点E是对角线AC上一点，连接DE、EF、DF，使△DEF是等腰直角三角形，DF交AC于点G.请直接写出线段AG、GE、EC三者之间满足的数量关系.

22．（10分）计算：+（﹣1）2﹣

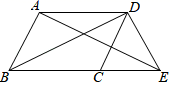
23．（12分）如图，在▱ABCD中，E是BC延长线上的一点，且DE＝AB，连接AE、BD，证明AE＝BD．

参考答案

一、选择题：本大题共12个小题，每小题3分，共36分.在每小题给出的四个选项中，只有一项是符合题目要求的.

1、A

2、A

3、D

4、B

5、B

6、D

7、D

8、D

9、C

10、C

11、C

12、A

二、填空题（每题4分，满分20分，将答案填在答题纸上）

13、

14、

15、1

16、①②③⑤

17、四

三、解答题 （本大题共7小题，共64分.解答应写出文字说明、证明过程或演算步骤.）

18、（1）见解析；（2）.

19、（1）见解析；（2）

20、（1）10  （2）  （3）或

21、（1）①详见解析；②60°．（1）IH＝FH；（3）EG1＝AG1+CE1．

22、1

23、见解析