


上海市闵行区信宏中学2022-2023学年七下数学期末质量检测试题含答案
展开
这是一份上海市闵行区信宏中学2022-2023学年七下数学期末质量检测试题含答案,共7页。试卷主要包含了在平面直角坐标系中,点在等内容,欢迎下载使用。
上海市闵行区信宏中学2022-2023学年七下数学期末质量检测试题(时间:120分钟 分数:120分) 学校_______ 年级_______ 姓名_______ 注意事项:1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其它答案标号。回答非选择题时,将答案写在答题卡上,写在本试卷上无效。3.考试结束后,将本试卷和答题卡一并交回。 一、选择题(每小题3分,共30分)1.下列几何图形是中心对称图形的是( )A.![]() B.
B. C.
C.![]() D.
D.![]() 2.若函数
2.若函数![]() 的图象与坐标轴有三个交点,则b的取值范围是
的图象与坐标轴有三个交点,则b的取值范围是![]()
![]() A.
A.![]() 且
且![]() B.
B.![]() C.
C.![]() D.
D.![]() 3.已知
3.已知![]() 是一元二次方程
是一元二次方程![]() 的一个实数根,则
的一个实数根,则![]() 的取值范围为( )A.
的取值范围为( )A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 4.已知某四边形的两条对角线相交于点O.动点P从点A出发,沿四边形的边按A→B→C的路径匀速运动到点C.设点P运动的时间为x,线段OP的长为y,表示y与x的函数关系的图象大致如图所示,则该四边形可能是( )
4.已知某四边形的两条对角线相交于点O.动点P从点A出发,沿四边形的边按A→B→C的路径匀速运动到点C.设点P运动的时间为x,线段OP的长为y,表示y与x的函数关系的图象大致如图所示,则该四边形可能是( )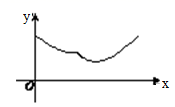 A.
A.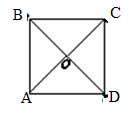 B.
B.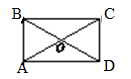 C.
C.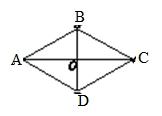 D.
D.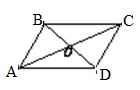 5.在△ABC和△DEF中,AB=2DE,AC=2DF,∠A=∠D,如果△ABC的周长是16,面积是12,那么△DEF的周长、面积依次为( )A.8,3 B.8,6 C.4,3 D.4,66.如图,在平面直角坐标系中,已知点A (1, 3), B(n, 3), 若直线y=2x与线段AB有公共点,则n的值不可能是( )
5.在△ABC和△DEF中,AB=2DE,AC=2DF,∠A=∠D,如果△ABC的周长是16,面积是12,那么△DEF的周长、面积依次为( )A.8,3 B.8,6 C.4,3 D.4,66.如图,在平面直角坐标系中,已知点A (1, 3), B(n, 3), 若直线y=2x与线段AB有公共点,则n的值不可能是( )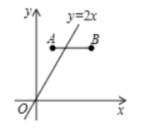 A.1.4 B.1.5 C.1.6 D.1.77.下列各组数据中,能做为直角三角形三边长的是( )。A.1、2、3 B.3、5、7 C.32,42,52 D.5、12、138.如图,点P是∠AOB的角平分线上一点,过点P作PC⊥OA于点C,且PC=3,则点P到OB的距离为( )
A.1.4 B.1.5 C.1.6 D.1.77.下列各组数据中,能做为直角三角形三边长的是( )。A.1、2、3 B.3、5、7 C.32,42,52 D.5、12、138.如图,点P是∠AOB的角平分线上一点,过点P作PC⊥OA于点C,且PC=3,则点P到OB的距离为( )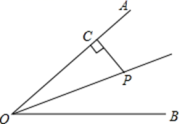 A.3 B.4 C.5 D.69.在平面直角坐标系中,点
A.3 B.4 C.5 D.69.在平面直角坐标系中,点![]() 在
在![]()
![]() A.第一象限 B.第二象限 C.第三象限 D.第四象限10.某超市一月份的营业额为200万元,已知第一季度的总营业额共1000万元,如果平均每月增长率为x,则由题意列方程应为( )A.200(1+x)2=1000B.200+200×2x=1000C.200+200×3x=1000D.200[1+(1+x)+(1+x)2]=1000二、填空题(本大题共有6小题,每小题3分,共18分)11.如图,△ABC中,∠C=90°,AD平分∠BAC交BC于点D,BD:DC=2:1,BC=7.8cm,则D到AB的距离为____cm.
A.第一象限 B.第二象限 C.第三象限 D.第四象限10.某超市一月份的营业额为200万元,已知第一季度的总营业额共1000万元,如果平均每月增长率为x,则由题意列方程应为( )A.200(1+x)2=1000B.200+200×2x=1000C.200+200×3x=1000D.200[1+(1+x)+(1+x)2]=1000二、填空题(本大题共有6小题,每小题3分,共18分)11.如图,△ABC中,∠C=90°,AD平分∠BAC交BC于点D,BD:DC=2:1,BC=7.8cm,则D到AB的距离为____cm.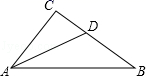 12.如图,一块矩形铁皮的长是宽的2倍,将这个铁皮的四角各剪去一个边长为3cm的小正方形,做成一个无盖的盒子,若盒子的容积是240cm3,则原铁皮的宽为______cm.
12.如图,一块矩形铁皮的长是宽的2倍,将这个铁皮的四角各剪去一个边长为3cm的小正方形,做成一个无盖的盒子,若盒子的容积是240cm3,则原铁皮的宽为______cm. 13.如图,已知一根长8m的竹竿在离地3m处断裂,竹竿顶部抵着地面,此时,顶部距底部有____m.
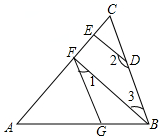
13.如图,已知一根长8m的竹竿在离地3m处断裂,竹竿顶部抵着地面,此时,顶部距底部有____m.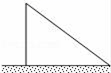 14.如图,
14.如图,![]() 于点E,
于点E,![]() 于点F,
于点F,![]() ,求证:
,求证:![]() .试将下面的证明过程补充完整
.试将下面的证明过程补充完整![]() 填空
填空![]() :证明:
:证明:![]() ,
,![]() 已知
已知![]()
![]() ______
______![]()
![]() 同位角相等,两直线平行
同位角相等,两直线平行![]() ,
,![]() 两直线平行,同旁内角互补
两直线平行,同旁内角互补![]() ,又
,又![]() 已知
已知![]() ,
,![]() ______,
______,![]() 同角的补角相等
同角的补角相等![]()
![]() ______
______![]() 内错角相等,两直线平行
内错角相等,两直线平行![]() ,
,![]() ______
______![]()
 15.已知一组数据3,7,7,5,x的平均数是5,那么这组数据的方差是_________.16.如图所示,过y轴正半轴上的任意一点P,作x轴的平行线,分别与反比例函数
15.已知一组数据3,7,7,5,x的平均数是5,那么这组数据的方差是_________.16.如图所示,过y轴正半轴上的任意一点P,作x轴的平行线,分别与反比例函数![]() 的图象交于点A和点B,若点C是x轴上任意一点,连接AC、BC,则△ABC的面积为_________.
的图象交于点A和点B,若点C是x轴上任意一点,连接AC、BC,则△ABC的面积为_________.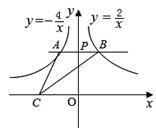 三、解下列各题(本大题共8小题,共72分)17.(8分)已知反比例函数
三、解下列各题(本大题共8小题,共72分)17.(8分)已知反比例函数![]() 的图象与一次函数
的图象与一次函数![]() 的图象交于点A(1,4)和点B(
的图象交于点A(1,4)和点B(![]() ,
,![]() ).
).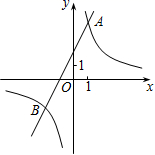 (1)求这两个函数的表达式;(2)观察图象,当
(1)求这两个函数的表达式;(2)观察图象,当![]() >0时,直接写出
>0时,直接写出![]() >
>![]() 时自变量
时自变量![]() 的取值范围;(3)如果点C与点A关于
的取值范围;(3)如果点C与点A关于![]() 轴对称,求△ABC的面积. 18.(8分)解方程(1)
轴对称,求△ABC的面积. 18.(8分)解方程(1)![]() +
+![]() =3 (2)
=3 (2) ![]() 19.(8分)化简求值:
19.(8分)化简求值:![]() ,从
,从![]() 的值:0,1,2中选一个代入求值. 20.(8分)解下列方程(1)
的值:0,1,2中选一个代入求值. 20.(8分)解下列方程(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() . 21.(8分)关于x的方程ax2+bx+c=0(a
. 21.(8分)关于x的方程ax2+bx+c=0(a![]() 0).(1)已知a,c异号,试说明此方程根的情况.(2)若该方程的根是x1=-1,x2=3,试求方程a(x+2)2+bx+2b+c=0的根. 22.(10分)国务院总理温家宝2011年11月16日主持召开国务院常务会议,会议决定建立青海三江源国家生态保护综合实验区.现要把228吨物资从某地运往青海甲、乙两地,用大、小两种货车共18辆,恰好能一次性运完这批物资.已知这两种货车的载重量分别为16吨/辆和10吨/辆,运往甲、乙两地的运费如下表:运往地
0).(1)已知a,c异号,试说明此方程根的情况.(2)若该方程的根是x1=-1,x2=3,试求方程a(x+2)2+bx+2b+c=0的根. 22.(10分)国务院总理温家宝2011年11月16日主持召开国务院常务会议,会议决定建立青海三江源国家生态保护综合实验区.现要把228吨物资从某地运往青海甲、乙两地,用大、小两种货车共18辆,恰好能一次性运完这批物资.已知这两种货车的载重量分别为16吨/辆和10吨/辆,运往甲、乙两地的运费如下表:运往地
车 型
甲 地(元/辆)
乙 地(元/辆)
大货车
720
800
小货车
500
650
(1)求这两种货车各用多少辆?(2)如果安排9辆货车前往甲地,其余货车前往乙地,设前往甲地的大货车为a辆,前往甲、乙两地的总运费为w元,求出w与a的函数关系式(写出自变量的取值范围);(3)在(2)的条件下,若运往甲地的物资不少于120吨,请你设计出使总运费最少的货车调配方案,并求出最少总运费. 23.(10分)已知:如图Rt△ABC中,∠ACB=90°,CD为∠ACB的平分线,DE⊥BC于点E,DF⊥AC于点F.求证:四边形CEDF是正方形.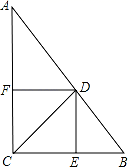 24.(12分)某文具店用1050元购进第一批某种钢笔,很快卖完,又用1440元购进第二批该种钢笔,但第二批每支钢笔的进价是第一批进价的1.2倍,数量比第一批多了10支.(1)求第一批每支钢笔的进价是多少元?(2)第二批钢笔按24元/支的价格销售,销售一定数量后,根据市场情况,商店决定对剩余的钢笔全按8折一次性打折销售,但要求第二批钢笔的利润率不低于20%,问至少销售多少支后开始打折? 参考答案 一、选择题(每小题3分,共30分)1、D2、A3、B4、D5、A6、A7、D8、A9、D10、D 二、填空题(本大题共有6小题,每小题3分,共18分)11、2.112、1.13、114、垂直的定义;
24.(12分)某文具店用1050元购进第一批某种钢笔,很快卖完,又用1440元购进第二批该种钢笔,但第二批每支钢笔的进价是第一批进价的1.2倍,数量比第一批多了10支.(1)求第一批每支钢笔的进价是多少元?(2)第二批钢笔按24元/支的价格销售,销售一定数量后,根据市场情况,商店决定对剩余的钢笔全按8折一次性打折销售,但要求第二批钢笔的利润率不低于20%,问至少销售多少支后开始打折? 参考答案 一、选择题(每小题3分,共30分)1、D2、A3、B4、D5、A6、A7、D8、A9、D10、D 二、填空题(本大题共有6小题,每小题3分,共18分)11、2.112、1.13、114、垂直的定义;![]() ;BC;两直线平行,同位角相等 15、0.2616、1. 三、解下列各题(本大题共8小题,共72分)17、(1)反比例函数的表达式为
;BC;两直线平行,同位角相等 15、0.2616、1. 三、解下列各题(本大题共8小题,共72分)17、(1)反比例函数的表达式为![]() ;一次函数的表达式为
;一次函数的表达式为![]() (2)0<
(2)0<![]() <1;(3)418、 (1)x=
<1;(3)418、 (1)x=![]() ;(2)x=119、2.20、(1)
;(2)x=119、2.20、(1)![]() ;(2)
;(2)![]() ,
,![]() ;(3)
;(3)![]() ,
,![]() .21、(1)见解析;(2)x=-3或x=122、(1)大货车用8辆,小货车用1辆(2)w=70a+11220(0≤a≤8且为整数)(3)使总运费最少的调配方案是:2辆大货车、4辆小货车前往甲地;3辆大货车、6辆小货车前往乙地.最少运费为3元23、证明见解析24、(1)15元;(2)1支.
.21、(1)见解析;(2)x=-3或x=122、(1)大货车用8辆,小货车用1辆(2)w=70a+11220(0≤a≤8且为整数)(3)使总运费最少的调配方案是:2辆大货车、4辆小货车前往甲地;3辆大货车、6辆小货车前往乙地.最少运费为3元23、证明见解析24、(1)15元;(2)1支.
相关试卷
这是一份上海市闵行区信宏中学2023-2024学年九上数学期末教学质量检测试题含答案,共7页。试卷主要包含了下列说法正确的是等内容,欢迎下载使用。
这是一份上海市闵行区信宏中学2023-2024学年八上数学期末学业质量监测试题含答案,共7页。试卷主要包含了下列运算正确的是,若分式的值为0,则x的值为等内容,欢迎下载使用。
这是一份上海市闵行区名校2022-2023学年七下数学期末监测模拟试题含答案,共7页。试卷主要包含了考生必须保证答题卡的整洁等内容,欢迎下载使用。








