上海市闵行区上虹中学2022-2023学年数学七年级第二学期期末达标测试试题含答案

上海市闵行区上虹中学2022-2023学年数学七年级第二学期期末达标测试试题

（时间：120分钟             分数：120分）

学校_______            年级_______        姓名_______

注意事项：

1．答卷前，考生务必将自己的姓名、准考证号填写在答题卡上。

2．回答选择题时，选出每小题答案后，用铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其它答案标号。回答非选择题时，将答案写在答题卡上，写在本试卷上无效。

3．考试结束后，将本试卷和答题卡一并交回。

一、选择题：本大题共12个小题，每小题3分，共36分.在每小题给出的四个选项中，只有一项是符合题目要求的.

1．下面几种说法：①对角线互相垂直的四边形是菱形；②一组对边平行，一组邻边相等的四边形是菱形；③对角线相等的平行四边形是矩形；④对角线互相垂直平分的四边形是菱形，那么准确的说法是（    ）

A．①②③ B．②③ C．③④ D．②④

2．关于的一次函数的图象可能正确的是（ ）

A． B． C． D．

3．甲、乙、丙、丁四人进行射箭测试，每人10次射箭成绩的平均成绩都相同，方差分别是S甲2=0.65，S乙2=0.55，S丙2=0.50，S丁2=0.45，则射箭成绩最稳定的是（　　）

A．甲 B．乙 C．丙 D．丁

4．若一组数据1.2.3.x的极差是6，则x的值为(    ).

A．7 B．8 C．9 D．7或

5．将矩形纸片ABCD按如图所示的方式折叠，得到菱形AECF，若AB=3，则BC的长为（　　）

A． B． C．1 D．2

6．在□ABCD中，∠A、∠B的度数之比为5∶4，则∠C等于（    ）

A．60° B．80° C．100° D．120°

7．如图．在正方形中，为边的中点，为上的一个动点，则的最小值是(     )

A． B． C． D．

8．如图，下列条件中，不能判定△ACD∽△ABC的是（　　）

A．∠ADC＝∠ACB B．∠B＝∠ACD C．∠ACD＝∠BCD D．

9．已知一组数据：10，8，6，10，8，13，11，12，10，10，7，9，8，12，9，11，12，9，10，11，则分组后频率为0.2的一组是（　　）

A．6～7    B．8～9    C．10～11    D．12～13

10．若关于x的方程的一个根是3，则m-n的值是

A．-1 B．-3 C．1 D．3

11．下列说法：矩形的对角线互相垂直且平分；菱形的四边相等；一组对边平行，另一组对边相等的四边形是平行四边形；正方形的对角线相等，并且互相垂直平分．其中正确的个数是（     ）

A．个 B．个 C．个 D．个

12．计算÷的结果是（   ）

A． B． C． D．

二、填空题（每题4分，满分20分，将答案填在答题纸上）

13．如果多边形的每个外角都是45°，那么这个多边形的边数是_____．

14．如图，已知一次函数y＝kx+b经过A（2，0），B（0，﹣1），当y＞0时，则x的取值范围是_____．

15．各内角所对边的长分别为、、，那么角的度数是________。

16．已知一直角三角形的两条直角边分别为6cm、8cm,则此直角三角形斜边上的高为____。

17．如图，菱形ABCD在平面直角坐标系中，点A位坐标原点，点B在x轴正半轴上，若点D的坐标为（1，），则点C的坐标为                 ．

三、解答题 （本大题共7小题，共64分.解答应写出文字说明、证明过程或演算步骤.）

18．（5分）解不等式组并求其整数解的和.

解：解不等式①，得_______；

解不等式②，得________；

把不等式①和②的解集在数轴上表示出来：

原不等式组的解集为________，

由数轴知其整数解为________，和为________.

在解答此题的过程中我们借助于数轴上，很直观地找出了原不等式组的解集及其整数解，这就是“数形结合的思想”，同学们要善于用数形结合的思想去解决问题.

19．（5分）社区利用一块矩形空地建了一个小型的惠民停车场，其布局如图所示.已知停车场的长为52米，宽为28米，阴影部分设计为停车位，要铺花砖，其余部分是等宽的通道.已知铺花砖的面积为640平方米.

（1）求通道的宽是多少米？

（2）该停车场共有车位64个，据调查分析，当每个车位的月租金为200元时，可全部租出；当每个车位的月租金每上涨10元，就会少租出1个车位.当每个车位的月租金上涨多少元时，停车场的月租金收入为14400元？

20．（8分）如图是一张长20cm、宽12cm的矩形纸板，将纸板四个角各剪去一个边长为cm的正方形，然后将四周突出部分折起，可制成一个无盖纸盒．

（1）这个无盖纸盒的长为　   　cm，宽为　   　cm；（用含x的式子表示）

（2）若要制成一个底面积是180m2的无盖长方体纸盒，求的值．

21．（10分）把直线向上平移m个单位后，与直线的交点为点P．

（1）求点P坐标用含m的代数式表示

（2）若点P在第一象限，求m的取值范围．

22．（10分）某校要从王同学和李同学中挑选一人参加县知识竞赛在五次选拔测试中他俩的成绩如下表．

根据上表解答下列问题：

(1)完成下表：

 (2)在这五次测试中，成绩比较稳定的同学是谁？若将80分以上的成绩视为优秀，则王同学、李同学在这五次测试中的优秀率各是多少？

(3)历届比赛表明，成绩达到80分以上(含80分)就很可能获奖，成绩达到90分以上(含90分)就很可能获得一等奖，那么你认为应选谁参加比赛比较合适？说明你的理由．

23．（12分）如图，在的网格中，网格线的公共点称为格点．已知格点、，如图所示线段上存在另外一个格点．

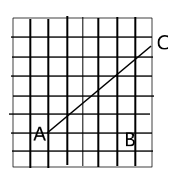
（1）建立平面直角坐标系，并标注轴、轴、原点；

（2）直接写出线段经过的另外一个格点的坐标：_____；

（3）用无刻度的直尺画图，运用所学的三角形全等的知识画出经过格点的射线，使（保留画图痕迹），并直接写出点的坐标：_____．

参考答案

一、选择题：本大题共12个小题，每小题3分，共36分.在每小题给出的四个选项中，只有一项是符合题目要求的.

1、C

2、C

3、D

4、D

5、A

6、C

7、A

8、C

9、D

10、B

11、B

12、C

二、填空题（每题4分，满分20分，将答案填在答题纸上）

13、1

14、x＞1

15、

16、4.8cm.

17、（3，）．

三、解答题 （本大题共7小题，共64分.解答应写出文字说明、证明过程或演算步骤.）

18、详见解析.

19、（1）6;（2）40或400

20、（1）（20﹣2x），（12﹣2x）；（2）1

21、（1）；（2）m>1.

22、（1）84　80　80　104；（2）小李．小王的优秀率为40%.小李的优秀率为80%；（3）小李，理由见解析

23、（1）如图所示见解析；（2）（5，4）；（3）.