上海市建平西学校2022-2023学年七年级数学第二学期期末考试模拟试题含答案

上海市建平西学校2022-2023学年七年级数学第二学期期末考试模拟试题

（时间：120分钟             分数：120分）

学校_______            年级_______        姓名_______

注意事项:

1．答题前，考生先将自己的姓名、准考证号码填写清楚，将条形码准确粘贴在条形码区域内。

2．答题时请按要求用笔。

3．请按照题号顺序在答题卡各题目的答题区域内作答，超出答题区域书写的答案无效；在草稿纸、试卷上答题无效。

4．作图可先使用铅笔画出，确定后必须用黑色字迹的签字笔描黑。

5．保持卡面清洁，不要折暴、不要弄破、弄皱，不准使用涂改液、修正带、刮纸刀。

一、选择题(每小题3分,共30分)

1．欧几里得是古希腊数学家，所著的《几何原本》闻名于世．在《几何原本》中，形如x2+ax＝b2的方程的图解法是：如图，以和b为直角边作Rt△ABC，再在斜边上截取BD＝，则图中哪条线段的长是方程x2+ax＝b2的解？答：是（    ） 

A．AC B．AD C．AB D．BC

2．已知一组数据2，3，4，x，1，4，3有唯一的众数4，则这组数据的中位数是(   )

A．2 B．3 C．4 D．5

3．如果一个三角形三条边的长分别是7，24，25，则这个三角形的最大内角的度数是（　　）

A．30° B．45° C．60° D．90°

4．如图，过正方形的顶点作直线，点、到直线的距离分别为和，则的长为(    )

A． B． C． D．

5．用反证法证明：“若整数系数一元二次方程ax2+bx+c=0（a≠0）有有理根，则a，b，c中至少有一个是偶数”，下列假设中正确的是（　　）

A．假设a，b，c都是偶数                                         B．假设a，b，c都不是偶数

C．假设a，b，c至多有一个是偶数                           D．假设a，b，c至多有两个是偶数

6．我国在近几年奥运会上所获金牌数（单位：枚）统计如下：

则这组数据的众数与中位数分别是（    ）

A．32、32 B．32、16 C．16、16 D．16、32

7．点P(-2，3)关于y轴的对称点的坐标是(     )

A．(2，3) B．(-2，3) C．(2，-3) D．(-2，-3)

8．若与最简二次根式是同类二次根式，则m的值为（　　）

A．7 B．11 C．2 D．1

9．把多项式ax3﹣2ax2+ax分解因式，结果正确的是（　　）

A．ax（x2﹣2x） B．ax2（x﹣2）

C．ax（x+1）（x﹣1） D．ax（x﹣1）2

10．若一组数据3、4、5、x、6、7的平均数是5，则x的值是（　　）

A．4 B．5 C．6 D．7

二、填空题(本大题共有6小题，每小题3分，共18分)

11．矩形的长和宽是关于的方程的两个实数根，则此矩形的对角线之和是________．

12．定义新运算：对于任意实数a，b都有：a⊕b=a（a﹣b）+1，其中等式右边是通常的加法、减法及乘法运算．如：2⊕5=2×（2﹣5）+1=2×（﹣3）+1=﹣5，那么不等式3⊕x＜13的解集为 ________.

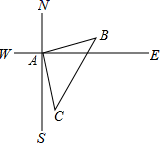
13．如图，在一次测绘活动中，某同学站在点A的位置观测停放于B、C两处的小船，测得船B在点A北偏东75°方向900米处，船C在点A南偏东15°方向1200米处，则船B与船C之间的距离为______米．

14．在盒子里放有三张分别写有整式a+1、a+2、2的卡片，从中随机抽取两张卡片，把两张卡片上的整式分别作为分子和分母，则能组成分式的概率是_____．

15．当m＝________时，函数y＝－(m－2)＋(m－4)是关于x的一次函数．

16．若是二次函数，则m=________ ．

三、解下列各题(本大题共8小题，共72分)

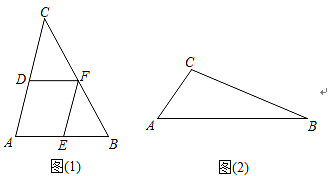
17．（8分）如果一个三角形满足条件：三角形的一个角与菱形的一个角重合，且菱形的这个角的对角顶点在三角形的这个角的对边上，则称这个菱形为该三角形的“亲密菱形”．如题（1），菱形AEFD为△ABC的“亲密菱形”．在图（2）中，请以∠BAC为重合角用直尺和圆规作出△ABC的“亲密菱形”AEFD．

18．（8分）矩形不一定具有的性质是（　　）

A．对角线互相平分 B．对角线互相垂直

C．对角线相等 D．是轴对称图形

19．（8分）如图，在平面直角坐标系中，Rt△ABC的三个顶点分别是A（-4, 1），B（-1,3），C（-1,1）

（1）将△ABC以原点O为旋转中心旋转180°，画出旋转后对应的△;平移△ABC，若A对应的点坐标为（-4，-5），画出△;

（2）若△绕某一点旋转可以得到△，直接写出旋转中心坐标是__________;

（3）在x轴上有一点P是的PA+PB的值最小，直接写出点P的坐标___________;

20．（8分）如图，△ABC的三个顶点的坐标分别为A(﹣2，3)、B(﹣6，0)、C(﹣1，0).

(1)画出把△ABC向下平移4个单位后的图形．

(2)画出将△ABC绕原点O按顺时针方向旋转90°后的图形．

(3)写出符合条件的以A、B、C、D为顶点的平行四边形的第四个顶点D的坐标．

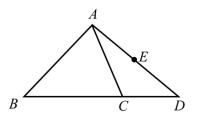
21．（8分）如图，在中，，点D在的延长线上，连接，E为的中点．请用尺规作图法在边上求作一点F，使得为的中位线．（保留作图痕迹，不写作法）

22．（10分）现在我们国家进入了高速发展的新时代，以为首的党中央在注重发展的同时，也提出了绿色中国的发展理念，请你以等腰三角形为基本图形利用平移或旋转设计一个宣传环保的图案，并加上简单的解说词．

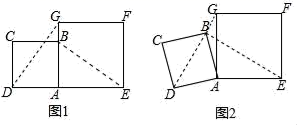
23．（10分）在数学兴趣小组活动中，小明进行数学探究活动．将大小不相同的正方形ABCD与正方形AEFG按图1位置放置，AD与AE在同一条直线上，AB与AG在同一条直线上．

（1）小明发现DG＝BE且DG⊥BE，请你给出证明；

（2）如图2，小明将正方形ABCD绕点A转动，当点B恰好落在线段DG上时

①猜想线段DG和BE的位置关系是　   　．

②若AD＝2，AE＝，求△ADG的面积．

24．（12分）某超市销售一种成本为40元千克的商品,若按50元千克销售,一个月可售出500千克,现打算涨价销售,据市场调查,涨价x元时,月销售量为m千克,m是x的一次函数,部分数据如下表：

观察表中数据,直接写出m与x的函数关系式：_______________：当涨价5元时,计算可得月销售利润是___________元；

当售价定多少元时,会获得月销售最大利润，求出最大利润．

参考答案

一、选择题(每小题3分,共30分)

1、B

2、B

3、D

4、A

5、B

6、C

7、A

8、C

9、D

10、B

二、填空题(本大题共有6小题，每小题3分，共18分)

11、1

12、x＞﹣1

13、192.2

14、．

15、－2

16、-1.

三、解下列各题(本大题共8小题，共72分)

17、见解析,

18、B

19、（1）见解析（2）（-1，-2）（3）P（-，0）.

20、 (1)见解析；(2)见解析；(3)D1(3，3)、D2(-7，3)、D3(-5，-3).

21、答案见解析

22、见解析.

23、（1）详见解析；（2）①DG⊥BE；②1.

24、 (1),6750;(2)70元,最大利润为9000元．