


2022-2023学年黑龙江省牡丹江市名校数学七年级第二学期期末质量跟踪监视模拟试题含答案
展开这是一份2022-2023学年黑龙江省牡丹江市名校数学七年级第二学期期末质量跟踪监视模拟试题含答案,共8页。试卷主要包含了计算的正确结果是等内容,欢迎下载使用。
2022-2023学年黑龙江省牡丹江市名校数学七年级第二学期期末质量跟踪监视模拟试题
(时间:120分钟 分数:120分)
学校_______ 年级_______ 姓名_______
注意事项:
1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其它答案标号。回答非选择题时,将答案写在答题卡上,写在本试卷上无效。
3.考试结束后,将本试卷和答题卡一并交回。
一、选择题(每小题3分,共30分)
1.如图,平行四边形ABCD的对角线AC与BD相交于点O,要使它成为矩形,需再添加的条件是( )
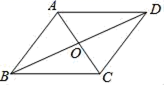
A.AO=OC B.AC=BD C.AC⊥BD D.BD平分∠ABC
2.如图1,将正方形![]() 置于平面直角坐标系中,其中
置于平面直角坐标系中,其中![]() 边在
边在![]() 轴上,其余各边均与坐标轴平行.直线
轴上,其余各边均与坐标轴平行.直线![]() 沿
沿![]() 轴的负方向以每秒1个单位的速度平移,在平移的过程中,该直线被正方形
轴的负方向以每秒1个单位的速度平移,在平移的过程中,该直线被正方形![]() 的边所截得的线段长为
的边所截得的线段长为![]() ,平移的时间为
,平移的时间为![]() (秒),
(秒),![]() 与
与![]() 的函数图象如图2所示,则图2中
的函数图象如图2所示,则图2中![]() 的值为( )
的值为( )
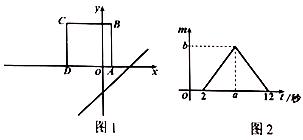
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
3.下列是最简二次根式的为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]() (a>0)
(a>0)
4.如图,在菱形ABCD中,AB=4,∠A=120°,点P,Q,K分别为线段BC,CD,BD上的任意一点,则PK+QK的最小值为( )
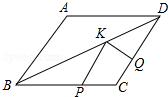
A.2 B.2![]() C.4 D.2
C.4 D.2![]() +2
+2
5.将下列长度的三根木棒首尾顺次连接,能组成直角三角形的是( )
A.1,2,3 B.4,6,8 C.6,8,10 D.5,5,4
6.计算![]() 的正确结果是( )
的正确结果是( )
A.![]() B.1 C.
B.1 C.![]() D.﹣1
D.﹣1
7.设x1、x2是方程x²+x-1=0的两根,则x1+x2=( )
A.-3 B.-1 C.1 D.3
8.下面的平面图形中,不能镶嵌平面的图形是( )
A.正三角形 B.正六边形 C.正四边形 D.正五边形
9.下列从左到右的变形是分解因式的是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
10.下列成语描述的事件为随机事件的是( )
A.守株待兔 B.水中捞月 C.瓮中捉鳖 D.水涨船高
二、填空题(本大题共有6小题,每小题3分,共18分)
11.已知平行四边形的周长是24,相邻两边的长度相差4,那么相邻两边的长分别是_____.
12.计算:![]() _________
_________
13.已知关于![]() 的方程
的方程![]() 会产生增根,则
会产生增根,则![]() __________.
__________.
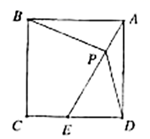
14.在正方形![]() 中,点
中,点![]() 在边
在边![]() 上,点
上,点![]() 在线段
在线段![]() 上,且
上,且![]() 则
则![]() _______度,四边形
_______度,四边形![]() 的面积
的面积![]() _________.
_________.
15.工人师傅给一幅长为![]() ,宽为
,宽为![]() 的矩形书法作品装裱,作品的四周需要留白如图所示,已知左、右留白部分的宽度一样,上、下留白部分的宽度也一样,而且左侧留白部分的宽度是上面留白部分的宽度的2倍,使得装裱后整个挂图的面积为
的矩形书法作品装裱,作品的四周需要留白如图所示,已知左、右留白部分的宽度一样,上、下留白部分的宽度也一样,而且左侧留白部分的宽度是上面留白部分的宽度的2倍,使得装裱后整个挂图的面积为![]() . 设上面留白部分的宽度为
. 设上面留白部分的宽度为![]() ,可列得方程为________。
,可列得方程为________。

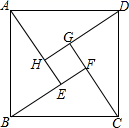
16.勾股定理,是几何学中一颗光彩夺目的明珠,被称为“几何学的基石”.中国是发现和研究勾股定理最古老的国家之一.中国古代数学家称直角三角形为勾股形,较短的直角边称为勾,另一直角边称为股,斜边称为弦,所以勾股定理也称为勾股弦定理.三国时期吴国赵爽创制了“勾股圆方图”(如图)证明了勾股定理.在这幅“勾股圆方图”中,大正方形ABCD是由4个全等的直角三角形再加上中间的那个小正方形EFGH组成的.若小正方形的边长是1,每个直角三角形的短的直角边长是3,则大正方形ABCD的面积是_____.
三、解下列各题(本大题共8小题,共72分)
17.(8分)规定两数a,b之间的一种运算,记作![]() ,如果
,如果![]() ,那么(a,b)=c,例如:因为21=8,所以(2,8)=1.
,那么(a,b)=c,例如:因为21=8,所以(2,8)=1.
(1)根据上述规定,填空:
![]() _____,
_____,![]() _____;
_____;
(2)小明在研究这种运算时发现一个现象,![]() ,小明给出了如下的证明:
,小明给出了如下的证明:
设![]() ,则
,则![]() ,即
,即![]() ,
,
∴![]() ,即
,即![]() ,
,
∴![]()
请你尝试用这种方法证明下面这个等式:![]()
18.(8分)计算
(1)![]()
(2)![]() ;
;
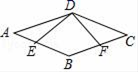
19.(8分)如图,已知四边形ABCD是平行四边形,点E,F分别是AB,BC上的点,AE=CF,并且∠AED=∠CFD.
求证:(1)△AED≌△CFD;
(2)四边形ABCD是菱形.
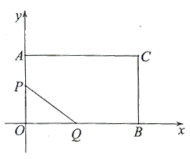
20.(8分)如图,在平面直角坐标系![]() 中,矩形
中,矩形![]() 的顶点
的顶点![]() 、
、![]() 在坐标轴上,点
在坐标轴上,点![]() 的坐标为
的坐标为![]() 点
点![]() 从点
从点![]() 出发,在折线段
出发,在折线段![]() 上以每秒3个单位长度向终点
上以每秒3个单位长度向终点![]() 匀速运动,点
匀速运动,点![]() 从点
从点![]() 出发,在折线段
出发,在折线段![]() 上以每秒4个单位长度向终点
上以每秒4个单位长度向终点![]() 匀速运动.两点同时出发,当其中一个点到达终点时,另一个点也停止运动,连接
匀速运动.两点同时出发,当其中一个点到达终点时,另一个点也停止运动,连接![]() .设两点的运动时间为
.设两点的运动时间为![]() ,线段
,线段![]() 的长度的平方为
的长度的平方为![]() ,即
,即![]() (单位长度2).
(单位长度2).
(1)当点![]() 运动到点
运动到点![]() 时,
时,![]() __________
__________![]() ,当点
,当点![]() 运动到点
运动到点![]() 时,
时,![]() __________
__________![]() ;
;
(2)求![]() 关于
关于![]() 的函数解析式,并直接写出自变量
的函数解析式,并直接写出自变量![]() 的取值范围.
的取值范围.
21.(8分)请用合适的方法解下列一元二次方程:
(1)![]() ;
;
(2)![]() .
.
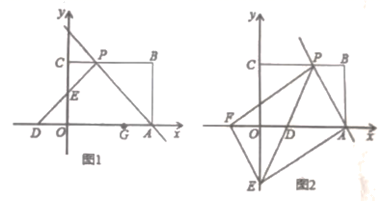
22.(10分)如图1,矩形![]() 摆放在平面直角坐标系中,点
摆放在平面直角坐标系中,点![]() 在
在![]() 轴上,点
轴上,点![]() 在
在![]() 轴上,
轴上,![]() ,
,![]() ,过点
,过点![]() 的直线交矩形
的直线交矩形![]() 的边
的边![]() 于点
于点![]() ,且点
,且点![]() 不与点
不与点![]() 、
、![]() 重合,过点
重合,过点![]() 作
作![]() ,
,![]() 交
交![]() 轴于点
轴于点![]() ,交
,交![]() 轴于点
轴于点![]() .
.
(1)若![]() 为等腰直角三角形.
为等腰直角三角形.
①求直线![]() 的函数解析式;
的函数解析式;
②在![]() 轴上另有一点
轴上另有一点![]() 的坐标为
的坐标为![]() ,请在直线
,请在直线![]() 和
和![]() 轴上分别找一点
轴上分别找一点![]() 、
、![]() ,使
,使![]() 的周长最小,并求出此时点
的周长最小,并求出此时点![]() 的坐标和
的坐标和![]() 周长的最小值.
周长的最小值.
(2)如图2,过点![]() 作
作![]() 交
交![]() 轴于点
轴于点![]() ,若以
,若以![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形是平行四边形,求直线
为顶点的四边形是平行四边形,求直线![]() 的解析式.
的解析式.
23.(10分)某单位要印刷“市民文明出行,遵守交通安全”的宣传材料.甲印刷厂提出:每份材料收1.5元印刷费,另收120元的制版费:乙印刷厂提出:每份材料收3元印刷费,不收制版费
设在同一家印刷厂一次印制数量为x份(x为正整数)
(1)根据题意,填写下表
一次印制数量(份) | 5 | 10 | 20 | … |
甲印刷厂收费(元) | 127.5 |
|
| … |
乙印刷厂收费(元) |
| 30 |
| … |
(2)设选择甲印刷厂的费用为y1元,选择乙印刷厂的费用为y2元,分别写出y1,y2关于x的函数关系式;
(3)在印刷品数量大于500份的情况下选哪家印刷厂印制省钱?请说明理由.
24.(12分)垃圾分类有利于对垃圾进行分流处理,能有效提高垃圾的资源价值和经济价值,力争物尽其用,为了了解同学们对垃圾分类相关知识的掌握情况,增强同学们的环保意识,某校对本校甲、乙两班各60名学生进行了垃极分类相关知识的测试,并分别随机抽取了15份成绩,整理分析过程如下,请补充完整
(收集数据)
甲班15名学生测试成绩统计如下:(满分100分)
68,72,89,85,82,85,74,92,80,85,78,85,69,76,80
乙班15名学生测试成绩统计如下:(满分100分)
86,89,83,76,73,78,67,80,80,79,80,84,82,80,83
(整理数据)
按如下分数段整理、描述这两组样本数据
组别 班级 | 65.6~70.5 | 70.5~75.5 | 75.5~80.5 | 80.5~85.5 | 85.5~90.5 | 90.5~95.5 |
甲班 | 2 | 2 | 4 | 5 | 1 | 1 |
乙班 | 1 | 1 | a | b | 2 | 0 |
在表中,a= ,b= .
(分析数据)
(1)两组样本数据的平均数、众数、中位数、方差如下表所示:
班级 | 平均数 | 众数 | 中位数 | 方差 |
甲班 | 80 | x | 80 | 47.6 |
乙班 | 80 | 80 | y | 26.2 |
在表中:x= ,y= .
(2)若规定得分在80分及以上(含80分)为合格,请估计乙班60名学生中垃圾分类相关知识合格的学生有 人
(3)你认为哪个班的学生掌握垃圾分类相关知识的情况较好,说明理由.
参考答案
一、选择题(每小题3分,共30分)
1、B
2、A
3、A
4、B
5、C
6、A
7、B
8、D
9、C
10、A
二、填空题(本大题共有6小题,每小题3分,共18分)
11、4和1
12、1
13、4
14、![]() ,
, ![]()
15、(120+4x)(40+2x)=1
16、25
三、解下列各题(本大题共8小题,共72分)
17、(1)1,0;(2)证明见解析.
18、(1)![]() +
+![]() ;(2)x1=5,x2=−1.
;(2)x1=5,x2=−1.
19、(1)证明见解析;(2)证明见解析.
20、(1)1,![]() ;(2)
;(2)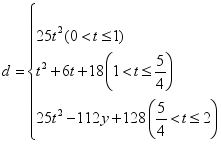 .
.
21、(1)![]() ,
,![]() ;(2)
;(2)![]() ,
,![]() .
.
22、(1)①直线![]() 解析式
解析式![]() , ②N(0,
, ②N(0,![]() ),
),![]() 周长的最小值为
周长的最小值为![]() ;(2)
;(2)![]() .
.
23、(1)135,150,15,60;(2)y1=120+1.5x, y2=3x;(3)在印刷品数量大于500份的情况下选甲家印刷厂印制省钱.
24、
相关试卷
这是一份黑龙江省七台河市名校2023-2024学年九上数学期末质量跟踪监视模拟试题含答案,共7页。试卷主要包含了若,那么的值是等内容,欢迎下载使用。
这是一份重庆市涪陵区名校2022-2023学年数学七年级第二学期期末质量跟踪监视模拟试题含答案,共7页。试卷主要包含了答题时请按要求用笔,下列点在直线上的是等内容,欢迎下载使用。
这是一份贵州省毕节地区名校2022-2023学年数学七年级第二学期期末质量跟踪监视模拟试题含答案,共8页。试卷主要包含了考生必须保证答题卡的整洁,五边形的内角和为,已知,则化简的结果是等内容,欢迎下载使用。












